Geschwindigkeit ist einfach ein Maß dafür, wie schnell oder langsam sich ein Objekt bewegt, etwa wie schnell Sie ein Auto fahren. Hier sprechen wir von einer bestimmten Art von Geschwindigkeit. Winkelgeschwindigkeit ist nur eine Geschwindigkeitsart, hier muss sich der Körper jedoch auf einer Kreisbahn bewegen.

Winkelgeschwindigkeitsformel

Die Winkelgeschwindigkeit ist definiert als die Änderungsrate der Winkelverschiebung, also des Winkels, den ein Körper auf einer Kreisbahn zurücklegt. Die Winkelgeschwindigkeit wird anhand der Anzahl der Drehungen/Umdrehungen berechnet, die ein Körper in der benötigten Zeit ausführt. Die Winkelgeschwindigkeit wird mit dem griechischen Buchstaben „ω“, bekannt als Omega, angegeben. Die SI-Einheit der Winkelgeschwindigkeit ist rad/s.

Die Winkelgeschwindigkeit wird mit zwei verschiedenen Formeln berechnet:

ω = θ/t ω = v/r

Formelableitung

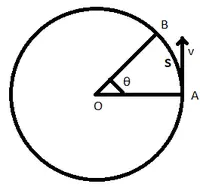
Betrachten wir einen Körper, der sich auf einer Kreisbahn mit dem oben gezeigten Radius r und einer linearen Geschwindigkeit v bewegt. Nehmen wir an, dass sich der Körper von Punkt A nach B bewegt und dabei eine Strecke s durch den Kreisbogen zurücklegt und einen Winkel θ in der Zeitspanne t zurücklegt.

Kreisbahn, die von einem Körper zurückgelegt wird

Bekanntlich ist die Winkelgeschwindigkeit die Änderungsrate der Verschiebung – Winkelgeschwindigkeit, ω = θ/t

Die Formel für die Winkelgeschwindigkeit lautet also ω = θ/t .

Eine andere Formel für die Winkelgeschwindigkeit

Trotz der oben genannten Formel gibt es eine andere und häufiger verwendete Formel zur Berechnung der Winkelgeschwindigkeit aus der Sicht von Wettbewerbsprüfungen.

Als ω = θ/t ⇢ (1)

Jetzt wissen wir, dass die über einen Kreisbogen zurückgelegte Strecke gleich dem Radius mal dem zurückgelegten Winkel ist. Also,

s = rθ

=> θ = s/r ⇢ (2)

Matrixprogramm in C-Sprache

Aus (1) und (2),

ω = s/(rt) ⇢ (3)

Auch aus dem allgemeinen Verständnis der linearen Geschwindigkeiten,

v = s/t ⇢ (4)

Aus (3) und (4),

ω = v/r

Beispielprobleme

Frage 1: Stellen Sie sich einen Körper vor, der sich auf einer Kreisbahn mit einem Radius von 5 m bewegt. Es deckt eine halbe Umdrehung in 5 Sekunden ab. Berechnen Sie seine Winkelgeschwindigkeit.

Lösung:

Bei einer halben Umdrehung beträgt der zurückgelegte Winkel 180 Grad. Im Bogenmaß ist es gleich π Bogenmaß.

ω = θ/t

=> ω = π/5 = 0,628 rad/s

Frage 2: Ein Autorad mit einem Radius von 2 m dreht sich mit einer linearen Geschwindigkeit von 10 m/s. Berechnen Sie die Winkelgeschwindigkeit.

Lösung:

ω = v/r

ω = 10/2

= 5 rad/s

Frage 3: Stellen Sie sich einen Rennwagen vor, der auf einer kreisförmigen Strecke mit einer Geschwindigkeit von 18 km/h und einem Streckenradius von 0,2 m fährt. Berechnen Sie die Winkelgeschwindigkeit des Autos.

Lösung:

v = 18 km/h = 5 m/s

r = 0,2 m

ω = v/r

= 5/0,2

= 25 rad/s

Frage 4: Ein Auto bewegt sich auf einer Kreisbahn mit einem Radius von 2 m und einer Winkelgeschwindigkeit von 2 rad/s. Berechnen Sie den Winkel in Grad, um den sich das Auto in 2 Sekunden bewegt.

Lösung:

Gegeben, ω = 2 rad/s und t = 2s

Da ω = θ/t => θ = ωt

=> θ = (2 × 2) = 4 rad

In Grad: θ = 4 × (180/π) = 229,18 Grad

Frage 5: Wie viele Umdrehungen hat ein Körper auf einer Kreisbahn mit einer Winkelgeschwindigkeit von 7π rad/s in 0,5 s gemacht?

Lösung:

Gegeben sei ω = 7π rad/s und t = 0,5s

Da ω = θ/t => θ = ωt

θ = (7π × 0,5) = 3,5π

Bei 2π rad beträgt die abgedeckte Umdrehung 1

=> In 1 rad beträgt die abgedeckte Umdrehung (1/2π)

=> Bei 3,5π rad sind Umdrehungen = 3,5π/2π = 1,75 Umdrehungen

Der Körper wird also in einem Zeitraum von 0,5 s eine vollständige Umdrehung und drei Viertel der nächsten Umdrehung durchführen.

Frage 6: Wie groß ist die Winkelgeschwindigkeit eines Körpers, der sich auf einer Kreisbahn mit einem Radius von 2 m bewegt, die 4 m und eine Bogenlänge von 5 s abdeckt?

Lösung:

Gegeben sei s = 4m, r = 2m, t = 5s

Unter Verwendung der Formel s = rθ => θ = s/r

θ = 4/2 = 2 rad

Da ω = θ/t

So konvertieren Sie einen String in einen Integer-Java

=> ω = 2/5 = 0,4 rad/s