Vor dem Verstehen B-Baum Und B+ Baum Aufgrund der Unterschiede sollten wir den B-Baum und den B+-Baum getrennt kennen.
Was ist der B-Baum?
B-Baum ist ein selbstausgleichender Baum und ein m-Wege-Baum, wobei m die Reihenfolge des Baums definiert. Btree ist eine Verallgemeinerung des Binärer Suchbaum Dabei kann ein Knoten je nach Wert von mehr als einen Schlüssel und mehr als zwei untergeordnete Elemente haben M . Im B-Baum werden die Daten in einer sortierten Reihenfolge angegeben, mit niedrigeren Werten im linken Teilbaum und höheren Werten im rechten Teilbaum.
String zum Char in Java
Eigenschaften des B-Baums
Das Folgende sind die Eigenschaften des B-Baums:
- Im B-Baum müssen sich alle Blattknoten auf der gleichen Ebene befinden, während im Fall eines Binärbaums die Blattknoten auf unterschiedlichen Ebenen liegen können.
Lassen Sie uns diese Eigenschaft anhand eines Beispiels verstehen.
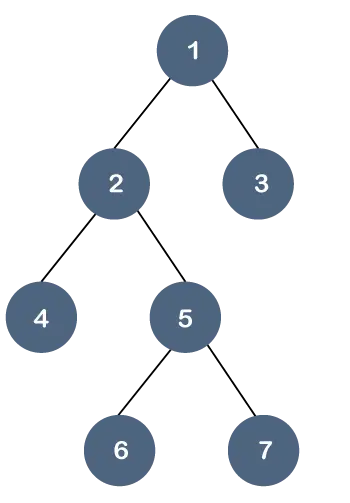
Im obigen Baum befinden sich nicht alle Blattknoten auf derselben Ebene, aber sie haben die beiden äußersten untergeordneten Knoten. Daher können wir sagen, dass der obige Baum ein ist Binärbaum aber kein B-Baum.
- Wenn der B-Baum eine Ordnung von m hat, kann jeder Knoten maximal haben M Bei minimalen Kindern haben die Blattknoten null Kinder, der Wurzelknoten zwei Kinder und die internen Knoten haben eine Obergrenze von m/2.
- Jeder Knoten kann maximal (m-1) Schlüssel haben. Wenn der Wert von m beispielsweise 5 ist, beträgt der maximale Wert der Schlüssel 4.
- Der Wurzelknoten hat mindestens einen Schlüssel, während alle anderen Knoten außer dem Wurzelknoten (Obergrenze von m/2 minus - 1) Mindestschlüssel haben.
- Wenn wir das Einfügen im B-Baum durchführen, wird der Knoten immer in den Blattknoten eingefügt.
Angenommen, wir möchten einen B-Baum der Ordnung 3 erstellen, indem wir Werte von 1 bis 10 einfügen.
Schritt 1: Zuerst erstellen wir einen Knoten mit 1 Wert, wie unten gezeigt:

Schritt 2: Das nächste Element ist 2, das wie unten gezeigt nach 1 kommt:

Schritt 3: Das nächste Element ist 3 und wird wie unten gezeigt nach 2 eingefügt:

Da wir wissen, dass jeder Knoten maximal 2 Schlüssel haben kann, teilen wir diesen Knoten durch das mittlere Element auf. Das mittlere Element ist 2 und wird daher zu seinem übergeordneten Element verschoben. Der Knoten 2 hat keinen übergeordneten Knoten und wird daher zum Stammknoten, wie unten gezeigt:

Schritt 4: Das nächste Element ist 4. Da 4 größer als 2 und 3 ist, wird es wie unten gezeigt nach der 3 hinzugefügt:

Schritt 5: Das nächste Element ist 5. Da 5 größer als 2, 3 und 4 ist, wird es nach 4 hinzugefügt, wie unten gezeigt:

Da wir wissen, dass jeder Knoten maximal 2 Schlüssel haben kann, teilen wir diesen Knoten durch das mittlere Element auf. Das mittlere Element ist 4 und wird daher zu seinem übergeordneten Element verschoben. Der übergeordnete Knoten ist Knoten 2; Daher werden 4 nach 2 hinzugefügt, wie unten gezeigt:

Schritt 6: Das nächste Element ist 6. Da 6 größer als 2, 4 und 5 ist, kommt 6 nach 5, wie unten gezeigt:

Schritt 7: Das nächste Element ist 7. Da 7 größer als 2, 4, 5 und 6 ist, kommt 7 nach 6, wie unten gezeigt:

Da wir wissen, dass jeder Knoten maximal 2 Schlüssel haben kann, teilen wir diesen Knoten durch das mittlere Element auf. Das mittlere Element ist 6 und wird daher wie unten gezeigt zu seinem übergeordneten Element verschoben:

Nach 4 kann jedoch nicht 6 hinzugefügt werden, da der Knoten maximal 2 Schlüssel haben kann. Daher teilen wir diesen Knoten durch das mittlere Element auf. Das mittlere Element ist 4 und wird daher zu seinem übergeordneten Element verschoben. Da Knoten 4 keinen übergeordneten Knoten hat, wird Knoten 4 wie unten gezeigt zum Stammknoten:

Was ist ein B+-Baum?
Der B+ Baum wird auch als fortgeschrittener selbstbalancierter Baum bezeichnet, da jeder Pfad von der Wurzel des Baums bis zum Blatt des Baums die gleiche Länge hat. Gleiche Länge bedeutet hier, dass alle Blattknoten auf der gleichen Ebene liegen. Es wird nicht vorkommen, dass einige der Blattknoten auf der dritten Ebene und einige auf der zweiten Ebene vorkommen.
Ein B+-Baumindex wird als mehrstufiger Index betrachtet, aber die B+-Baumstruktur ähnelt nicht den sequentiellen Dateien mit mehrstufigem Index.
Warum wird der B+-Baum verwendet?
Ein B+-Baum wird verwendet, um die Datensätze sehr effizient zu speichern, indem die Datensätze mithilfe der indizierten B+-Baumstruktur indiziert gespeichert werden. Durch die mehrstufige Indizierung wird der Datenzugriff schneller und einfacher.
B+-Baumknotenstruktur
Die Knotenstruktur des B+-Baums enthält Zeiger und Schlüsselwerte, die in der folgenden Abbildung dargestellt sind:

Wie wir in der obigen B+-Baumknotenstruktur beobachten können, enthält sie n-1 Schlüsselwerte (k1zu kn-1) und n Zeiger (S1SpitzeN).
Die Suchschlüsselwerte, die im Knoten platziert werden, werden in sortierter Reihenfolge gehalten. Wenn ich also
entspricht einer Zeichenfolge in Java
Einschränkung für verschiedene Knotentypen
Sei 'b' die Ordnung des B+-Baums.
Nicht-Blattknoten
Stellt 'm' die Anzahl der Kinder eines Knotens dar, dann kann die Beziehung zwischen der Reihenfolge des Baums und der Anzahl der Kinder wie folgt dargestellt werden:

Angenommen, k stellt die Suchschlüsselwerte dar. Die Beziehung zwischen der Reihenfolge des Baums und dem Suchschlüssel kann wie folgt dargestellt werden:
Da wir wissen, dass die Anzahl der Zeiger gleich den Suchschlüsselwerten plus 1 ist, kann es mathematisch wie folgt geschrieben werden:
Anzahl der Zeiger (oder untergeordneten Elemente) = Anzahl der Suchschlüssel + 1
Daher wäre die maximale Anzahl von Zeigern „b“ und die minimale Anzahl von Zeigern wäre die Deckenfunktion von b/2.
Blattknoten
Ein Blattknoten ist ein Knoten, der auf der letzten Ebene des B+-Baums auftritt, und jeder Blattknoten verwendet nur einen Zeiger, um sich miteinander zu verbinden und den sequentiellen Zugriff auf der Blattebene bereitzustellen.
Im Blattknoten beträgt die maximale Anzahl untergeordneter Elemente:

Die maximale Anzahl an Suchschlüsseln beträgt:

Wurzelknoten
Die maximale Anzahl an Kindern im Fall des Wurzelknotens beträgt: b
Die Mindestanzahl der Kinder beträgt: 2
Sonderfälle im B+-Baum
Fall 1: Wenn der Wurzelknoten der einzige Knoten im Baum ist. In diesem Fall wird der Wurzelknoten zum Blattknoten.
In diesem Fall ist die maximale Anzahl von Kindern 1, d. h. der Wurzelknoten selbst, während die minimale Anzahl von Kindern b-1 ist, was der eines Blattknotens entspricht.
Darstellung eines Blattknotens im B+-Baum

In der obigen Abbildung ist '.' stellt den Zeiger dar, während 10, 20 und 30 die Schlüsselwerte sind. Der Zeiger enthält die Adresse, an der der Schlüsselwert gespeichert ist, wie in der obigen Abbildung dargestellt.
Beispiel eines B+-Baums

In der obigen Abbildung enthält der Knoten drei Schlüsselwerte, nämlich 9, 16 und 25. Der Zeiger, der vor 9 erscheint, enthält die durch k dargestellten Schlüsselwerte kleiner als 9ich. Der Zeiger, der vor 16 erscheint, enthält die Schlüsselwerte größer oder gleich 9, aber kleiner als 16, dargestellt durch kj. Der Zeiger, der vor 25 erscheint, enthält die durch k dargestellten Schlüsselwerte größer oder gleich 16, aber kleiner als 25N.
Unterschiede zwischen B-Baum und B+-Baum

Im Folgenden sind die Unterschiede zwischen dem B-Baum und dem B+-Baum aufgeführt:
| B-Baum | B+ Baum |
|---|---|
| Im B-Baum werden alle Schlüssel und Datensätze sowohl in internen als auch in Blattknoten gespeichert. | Im B+-Baum sind Schlüssel die in den internen Knoten gespeicherten Indizes und Datensätze werden in den Blattknoten gespeichert. |
| Im B-Baum können Schlüssel nicht wiederholt gespeichert werden, was bedeutet, dass es keine Duplizierung von Schlüsseln oder Datensätzen gibt. | Im B+-Baum kann es zu Redundanz beim Vorkommen der Schlüssel kommen. In diesem Fall werden die Datensätze in den Blattknoten gespeichert, während die Schlüssel in den internen Knoten gespeichert werden, sodass in den internen Knoten redundante Schlüssel vorhanden sein können. |
| Im Btree sind Blattknoten nicht miteinander verknüpft. | Im B+-Baum sind die Blattknoten miteinander verknüpft, um den sequentiellen Zugriff bereitzustellen. |
| In Btree ist die Suche nicht sehr effizient, da die Datensätze entweder in Blatt- oder internen Knoten gespeichert werden. | Im B+-Baum ist die Suche sehr effizient oder schneller, da alle Datensätze in den Blattknoten gespeichert sind. |
| Das Löschen interner Knoten ist sehr langsam und zeitaufwändig, da wir auch das untergeordnete Element des gelöschten Schlüssels berücksichtigen müssen. | Das Löschen im B+-Baum erfolgt sehr schnell, da alle Datensätze in den Blattknoten gespeichert werden, sodass wir das untergeordnete Element des Knotens nicht berücksichtigen müssen. |
| In Btree ist ein sequenzieller Zugriff nicht möglich. | Im B+-Baum sind alle Blattknoten durch einen Zeiger miteinander verbunden, sodass ein sequenzieller Zugriff möglich ist. |
| In Btree gilt: Je mehr Teilungsvorgänge ausgeführt werden, desto höher ist die Höhe im Vergleich zur Breite. | B+-Baum hat im Vergleich zur Höhe mehr Breite. |
| In Btree hat jeder Knoten mindestens zwei Zweige und jeder Knoten enthält einige Datensätze, sodass wir nicht bis zu den Blattknoten durchlaufen müssen, um die Daten zu erhalten. | Im B+-Baum enthalten interne Knoten nur Zeiger und Blattknoten enthalten Datensätze. Alle Blattknoten befinden sich auf derselben Ebene, daher müssen wir bis zu den Blattknoten durchlaufen, um die Daten zu erhalten. |
| Der Wurzelknoten enthält mindestens 2 bis m Kinder, wobei m die Ordnung des Baums ist. | Der Wurzelknoten enthält mindestens 2 bis m Kinder, wobei m die Ordnung des Baums ist. |
