Ein NFA kann null, eine oder mehr als eine Bewegung von einem bestimmten Zustand auf einem bestimmten Eingabesymbol haben. Ein NFA kann auch NULL-Züge (Züge ohne Eingabesymbol) haben. Andererseits hat DFA eine und nur eine Bewegung von einem bestimmten Zustand auf einem bestimmten Eingabesymbol.
Schritte zur Konvertierung von NFA in DFA:
Schritt 1: Konvertieren Sie den angegebenen NFA in die entsprechende Übergangstabelle
Um den NFA in die entsprechende Übergangstabelle umzuwandeln, müssen wir alle Zustände, Eingabesymbole und Übergangsregeln auflisten. Die Übergangsregeln werden in Form einer Matrix dargestellt, wobei die Zeilen den aktuellen Zustand, die Spalten das Eingabesymbol und die Zellen den nächsten Zustand darstellen.
Schritt 2: Erstellen Sie den Startstatus des DFA
Der Startzustand des DFA ist die Menge aller möglichen Startzustände im NFA. Dieser Satz wird als Epsilon-Abschluss des NFA-Startzustands bezeichnet. Der Epsilon-Abschluss ist die Menge aller Zustände, die vom Startzustand aus durch folgende Epsilon-(?)-Übergänge erreicht werden können.
Schritt 3: Erstellen Sie die Übergangstabelle des DFA
Die Übergangstabelle des DFA ähnelt der Übergangstabelle des NFA, jedoch stellen die Zeilen und Spalten anstelle einzelner Zustände eine Reihe von Zuständen dar. Für jedes Eingabesymbol enthält die entsprechende Zelle in der Übergangstabelle den Epsilon-Abschluss der Menge von Zuständen, die durch Befolgen der Übergangsregeln in der Übergangstabelle des NFA erhalten werden.
Schritt 4: Erstellen Sie die endgültigen Zustände des DFA
Die Endzustände des DFA sind die Zustandsmengen, die mindestens einen Endzustand des NFA enthalten.
Schritt 5: Vereinfachen Sie das DFA
Der in den vorherigen Schritten erhaltene DFA kann unnötige Zustände und Übergänge enthalten. Um den DFA zu vereinfachen, können wir die folgenden Techniken verwenden:
- Nicht erreichbare Zustände entfernen: Zustände, die vom Startzustand aus nicht erreichbar sind, können aus dem DFA entfernt werden.
- Tote Zustände entfernen: Zustände, die nicht zu einem endgültigen Zustand führen können, können aus dem DFA entfernt werden.
- Äquivalente Zustände zusammenführen: Zustände, die für alle Eingabesymbole dieselben Übergangsregeln haben, können zu einem einzigen Zustand zusammengeführt werden.
Schritt 6: Wiederholen Sie die Schritte 3–5, bis keine weitere Vereinfachung mehr möglich ist
Nach der Vereinfachung des DFA wiederholen wir die Schritte 3–5, bis keine weitere Vereinfachung mehr möglich ist. Der endgültig erhaltene DFA ist der minimierte DFA, der dem gegebenen NFA entspricht.
Beispiel: Betrachten Sie die folgende NFA, die in Abbildung 1 dargestellt ist.
sind Musterbeispiele

Im Folgenden sind die verschiedenen Parameter für NFA aufgeführt. Q = { q0, q1, q2 } ? = ( a, b ) F = { q2 } ? (Übergangsfunktion von NFA)
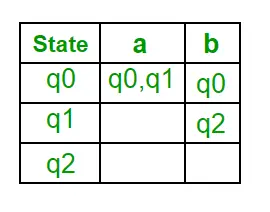
Schritt 1: Q’ = ? Schritt 2: Q’ = {q0} Schritt 3: Finden Sie für jeden Zustand in Q’ die Zustände für jedes Eingabesymbol. Derzeit ist der Zustand in Q‘ q0. Suchen Sie mithilfe der Übergangsfunktion von NFA nach Bewegungen von q0 auf den Eingabesymbolen a und b und aktualisieren Sie die Übergangstabelle von DFA. ?‘ (Übergangsfunktion von DFA)

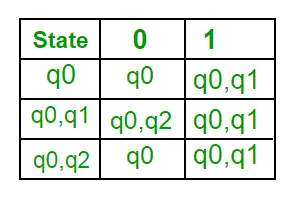
Jetzt wird { q0, q1 } als ein einzelner Zustand betrachtet. Da sein Eintrag nicht in Q‘ steht, fügen Sie ihn zu Q‘ hinzu. Also Q' = { q0, { q0, q1 } } Nun sind Bewegungen vom Zustand { q0, q1 } auf verschiedenen Eingabesymbolen nicht in der Übergangstabelle von DFA vorhanden, wir berechnen es wie folgt: ?' , a ) = ? ( q0, a )? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? ( q0, b )? ? ( q1, b ) = { q0, q2 } Jetzt aktualisieren wir die Übergangstabelle von DFA. ?‘ (Übergangsfunktion von DFA)

Jetzt wird { q0, q2 } als ein einzelner Zustand betrachtet. Da sein Eintrag nicht in Q‘ steht, fügen Sie ihn zu Q‘ hinzu. Also Q' = { q0, { q0, q1 }, { q0, q2 } } Nun sind Bewegungen vom Zustand {q0, q2} auf verschiedenen Eingabesymbolen nicht in der Übergangstabelle von DFA vorhanden, wir berechnen es wie folgt: ?' ( { q0, q2 }, a ) = ? ( q0, a )? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? ( q0, b )? ? ( q2, b ) = { q0 } Jetzt aktualisieren wir die Übergangstabelle von DFA. ?‘ (Übergangsfunktion von DFA)
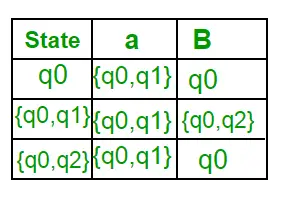
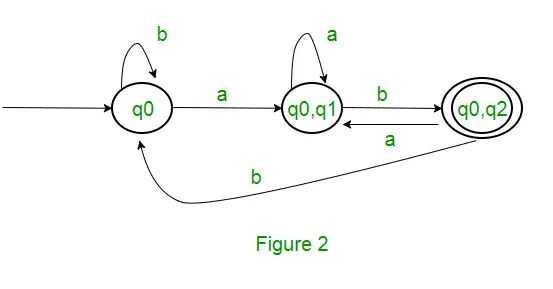
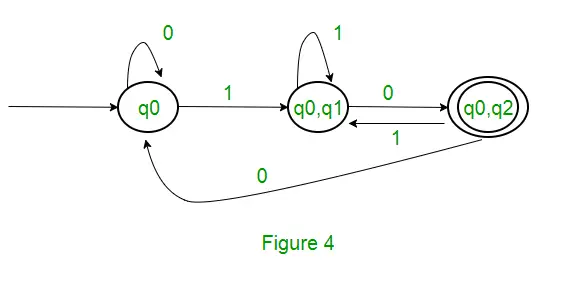
Da kein neuer Zustand generiert wird, sind wir mit der Konvertierung fertig. Der Endzustand von DFA ist der Zustand, dessen Komponente q2 ist, d. h. {q0, q2}. Im Folgenden sind die verschiedenen Parameter für DFA aufgeführt. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = ( a, b ) F = { { q0, q2 } } und Übergangsfunktion ?’ wie oben gezeigt. Der endgültige DFA für den oben genannten NFA ist in Abbildung 2 dargestellt.
Notiz : Manchmal ist es nicht einfach, reguläre Ausdrücke in DFA zu konvertieren. Zuerst können Sie reguläre Ausdrücke in NFA und dann NFA in DFA konvertieren.
Frage : Die Anzahl der Zustände im minimalen deterministischen endlichen Automaten, der dem regulären Ausdruck (0 + 1)* (10) entspricht, beträgt ____________.
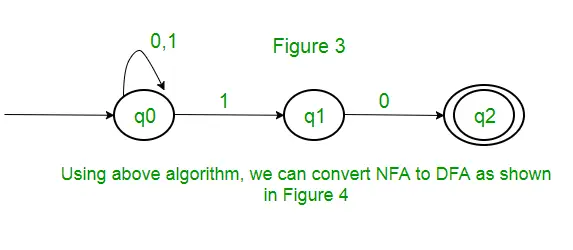
Lösung : Zuerst erstellen wir eine NFA für den obigen Ausdruck. Um einen NFA für (0 + 1)* zu erstellen, befindet sich der NFA am Eingabesymbol 0 oder 1 im gleichen Zustand q0. Anschließend fügen wir zur Verkettung zwei Bewegungen hinzu (q0 nach q1 für 1 und q1 nach q2 für 0), wie gezeigt in Abbildung 3.
Dieser Artikel wurde von Sonal Tuteja verfasst.
