KOTANGENSFORMEL

Die Trigonometrie ist ein wichtiger Zweig der Mathematik, der sich mit der Beziehung zwischen den Seitenlängen und den Winkeln eines rechtwinkligen Dreiecks beschäftigt. Sinus, Kosinus, Tangens, Kosekans, Sekante und Kotangens sind die sechs trigonometrischen Verhältnisse oder Funktionen. Dabei wird ein trigonometrisches Verhältnis als das Verhältnis zwischen den Seiten eines rechtwinkligen Dreiecks dargestellt.

sin θ = opposite side/hypotenuse
cos θ = Ankathete/Hypotenuse
tan θ = gegenüberliegende Seite/angrenzende Seite
cosec θ = 1/sin θ = Hypotenuse/Gegenkathete
sec θ = 1/cos θ = Hypotenuse/angrenzende Seite
cot θ = 1/tan θ = angrenzende Seite/gegenüberliegende Seite

Eine Kotangensfunktion ist eine Kehrfunktion der gegebenen Tangensfunktion. Der Wert eines Kotangenswinkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der Seite, die an den gegebenen Winkel angrenzt, zur Länge der Seite, die dem gegebenen Winkel gegenüberliegt. Wir schreiben die Kotangensfunktion als cot.

Dreieck ABC

Die Kotangensformel für den Winkel θ lautet nun:

cot θ = (Angrenzende Seite)/(Gegenüberliegende Seite)

Die Kotangensfunktion ist im ersten und dritten Quadranten positiv und im zweiten und vierten Quadranten negativ.

cot (2π + θ) = cot θ (1^stQuadrant)
Kinderbett (π – θ) = – Kinderbett θ (2^ndQuadrant)
Kinderbett (π + θ) = Kinderbett θ (3^rdQuadrant)
Kinderbett (2π – θ) = – Kinderbett θ (4^ThQuadrant)

Die Kotangensfunktion ist eine negative Funktion, da der Kotangens eines negativen Winkels das Negative eines positiven Kotangenswinkels ist.

Kinderbett (-θ) = – Kinderbett θ

In Bezug auf die Tangensfunktion wird die Kotangensfunktion wie folgt geschrieben:

cot θ = 1/tan θ

(oder)

cot θ = tan (90° – θ) (oder) tan (π/2 – θ)

Die Kotangensfunktion in Form von Sinus- und Kosinusfunktionen kann wie folgt geschrieben werden:

cot θ = cos θ/sin θ

Wir wissen, dass cot θ = angrenzende Seite/gegenüberliegende Seite ist

Teilen Sie nun Zähler und Nenner durch die Hypotenuse

⇒ cot θ = (angrenzende Seite/Hypotenuse) / (gegenüberliegende Seite/Hypotenuse)

Wir wissen, dass sin θ = gegenüberliegende Seite/Hypotenuse

cos θ = Ankathete/Hypotenuse

Daher ist cot θ = cos θ/sin θ

Die Kotangensfunktion im Sinne der Sinusfunktion kann geschrieben werden als:

Kinderbett θ = (√1 – Sünde ² i)/sünde i

Wir wissen, dass cot θ = cos θ/sin θ ist

Von den pythagoreischen Identitäten haben wir;

cos²θ + Sünde²θ = 1

⇒ cos θ = √1 – sin²ich

Daher ist cot θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Die Kotangensfunktion im Sinne der Kosinusfunktion kann geschrieben werden als:

cot θ = cos θ/(√1 -cos ² ich)

Wir wissen, dass cot θ = cos θ/sin θ ist

Von den pythagoreischen Identitäten haben wir;

cos²θ + Sünde²θ = 1

sin θ = √1 – cos²ich

Daher ist cot θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Die Kotangensfunktion in Form von Sekanten- und Kosekansfunktionen kann wie folgt geschrieben werden:

cot θ = cosec θ/sec θ

Wir haben cot θ = cos θ/sin θ

Dies kann wie folgt geschrieben werden: cot θ = (1/sin θ) / (1/cos θ)

⇒ cot θ = cosec θ/sec θ

Die Kotangensfunktion im Sinne der Kosekansfunktion kann wie folgt geschrieben werden:

cot θ = √(cosec ² - 1)

Aus den pythagoreischen Identitäten haben wir:

cosec²θ – Kinderbett²θ = 1

⇒ Kinderbett²θ = 1 – cosec²- 1

Daher ist cot θ = √(cosec²- 1)

Die Kotangensfunktion im Sinne der Sekantenfunktion kann wie folgt geschrieben werden:

cot θ = 1/(√sec ² ich – 1)

Aus den pythagoreischen Identitäten haben wir:

Sek²θ – also²θ = 1

tan θ = √sec²ich – 1

Wir wissen, dass cot θ = 1/tan θ ist

Somit, Kinderbett θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Trigonometrische Verhältnistabelle

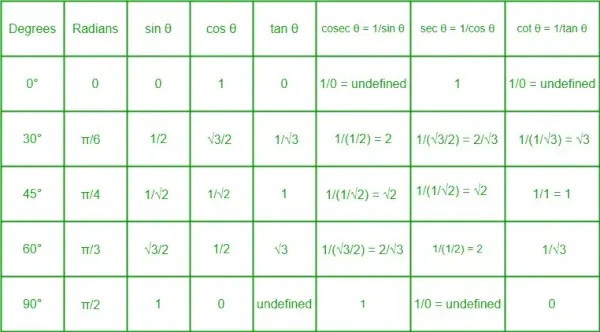
Trigonometrische Verhältnistabelle

Kotangensgesetz oder Gesetz der Kotangenten

Das Kotangensgesetz sieht ähnlich aus wie das Sinusgesetz, aber hier geht es um halbe Winkel. Das Kotangensgesetz beschreibt die Beziehung zwischen den Längen der Seiten des Dreiecks und den Kotangenten der Hälften der drei Winkel. Betrachten Sie ein Dreieck ABC, wobei a, b und c die Längen der Seiten des Dreiecks sind.

Das Kotangensgesetz besagt, dass

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Dabei ist s der Halbumfang des Dreiecks ABC und r sein Innenradius des eingeschriebenen Kreises des Dreiecks.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Beispielprobleme

Aufgabe 1: Finden Sie den Wert von cot θ, wenn tan θ = 3/4.

Lösung:

Gegebene Daten, tan θ = 3/4

Wir wissen das, cot θ = 1/tan θ

⇒ Kinderbett θ = 1/(3/4) = 4/3

So, cot θ = 4/3

Aufgabe 2: Finden Sie den Wert von cot α, sin α = 1/3 und cos α = 2√2/3.

Lösung:

Gegebene Daten, sin α = 1/3 und cos α = 2√2/3

Wir wissen das, cot α = cos α/sin α

⇒ Kinderbett α = (2√2/3) / (1/3) = 2√2

Daher ist der Wert von cot α = 2√2

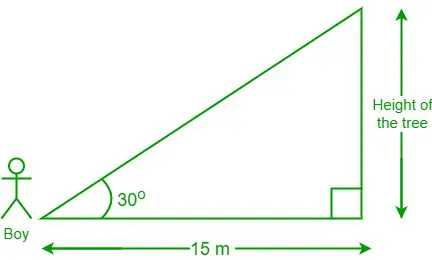
Problem 3: Ein Junge, der 15 m von einem Baum entfernt steht, blickt in einem 30-Grad-Winkel zur Baumspitze. Wie hoch ist der Baum?

Lösung:

Diagramm aus den angegebenen Daten

Angesichts der Daten beträgt der Abstand zwischen dem Jungen und dem Fuß des Baumes = 15 m und θ = 30°

Die Höhe des Baumes sei „h“

Wir haben, cot θ = angrenzende Seite/gegenüberliegende Seite

⇒ Kinderbett 30° = 15/h

⇒ √3 = 15/h [da cot 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Daher ist die Höhe des Baumes = 5√3 m

Aufgabe 4: Finden Sie den Wert von cot x, wenn sec x = 6/5.

Lösung:

Gegebene Daten, Sek. x = 6/5

Wir haben, Sek ² x – also ² x = 1

⇒ (6/5)²- Also²x = 1

⇒ 36/25 – also²x = 1

⇒ also²x = 36/25 – 1

⇒ also²x = 11/25

⇒ tan x = √(11/25) = √11/5

Wir wissen das, cot x = 1/tan x

⇒ Kinderbett x = 1/(√11/5) = 5/√11

Daher ist cot x = 5/√11

Aufgabe 5: Finden Sie den Wert von cot θ, wenn cosec θ = 25/24.

Lösung:

Gegebene Daten, cosec θ = 25/24

Wir wissen das, cot θ = √(cosec ² - 1)

⇒ Kinderbett θ = √(25/24)²- 1

⇒ cot θ =√(625 – 576)/576 = √49/576

⇒ Kinderbett θ = 7/24

Daher ist der Wert von cot θ = 7/24

Aufgabe 6: Finden Sie den Wert von cot β, wenn sin β = 5/13.

Lösung:

Gegebene Daten, sin β = 5/13

Wir wissen das, ohne ² β + cos ² β = 1

⇒ (5/13)²+ weil²β = 1
Powershell vs. Bash

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

cot β = cosβ/sin β

= (12/13) / (5/13)

⇒ Kinderbett β = 12/5

Daher ist der Wert von cot β = 12/5

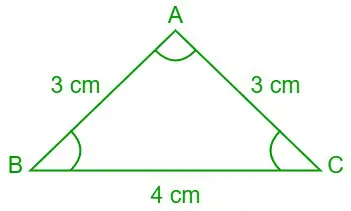
Aufgabe 7: Ermitteln Sie mithilfe des Kotangensgesetzes die Werte von ∠A, ∠B und ∠C (in Grad), wenn die Längen der drei Seiten des Dreiecks ABC a = 4 cm, b = 3 cm und c = betragen 3 cm.

Lösung:

Gegeben sei a = 4 cm, b = 3 cm und c = 3 cm

Dreieck ABC

Aus dem Kotangensgesetz

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Nun ist s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Inradius des Dreiecks r = 2/√5

Aus der Gleichung des Kotangensgesetzes

Kinderbett (A/2)/1 = 1/(2/√5)

⇒ Kinderbett (A/2) = √5/2 ⇒ A/2 = Kinderbett^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

Kinderbett(B/2)/2 = 1/(2/√5)

⇒ Kinderbett(B/2)/2 = √5/2 ⇒ Kinderbett (B/2) = √5

⇒ (B/2) = Kinderbett^-1(√5) = 24,1° ⇒ ∠B = 48,2°

Kinderbett (C/2)/2 = 1/(2/√5)

⇒ cot(C/2) = √5 ⇒ (C/2) = cot^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Daher betragen die Winkel des Dreiecks ABC ∠A = 83,6°, ∠B = 48,2° und ∠C = 48,2°.