Das Löschen eines Knotens aus einem AVL-Baum ähnelt dem in einem binären Suchbaum. Das Löschen kann den Gleichgewichtsfaktor eines AVL-Baums stören und daher muss der Baum neu ausgeglichen werden, um die AVL-Qualität aufrechtzuerhalten. Zu diesem Zweck müssen wir Rotationen durchführen. Die beiden Rotationsarten sind L-Rotation und R-Rotation. Hier werden wir R-Rotationen diskutieren. L-Rotationen sind die Spiegelbilder davon.

Wenn der zu löschende Knoten im linken Teilbaum des kritischen Knotens vorhanden ist, muss die L-Rotation angewendet werden, andernfalls befindet sich der zu löschende Knoten im rechten Teilbaum des kritischen Knotens , wird die R-Rotation angewendet.

Nehmen wir an, dass A der kritische Knoten und B der Wurzelknoten seines linken Unterbaums ist. Soll der Knoten X, der im rechten Teilbaum von A vorhanden ist, gelöscht werden, kann es drei verschiedene Situationen geben:

R0-Rotation (Knoten B hat Ausgleichsfaktor 0)

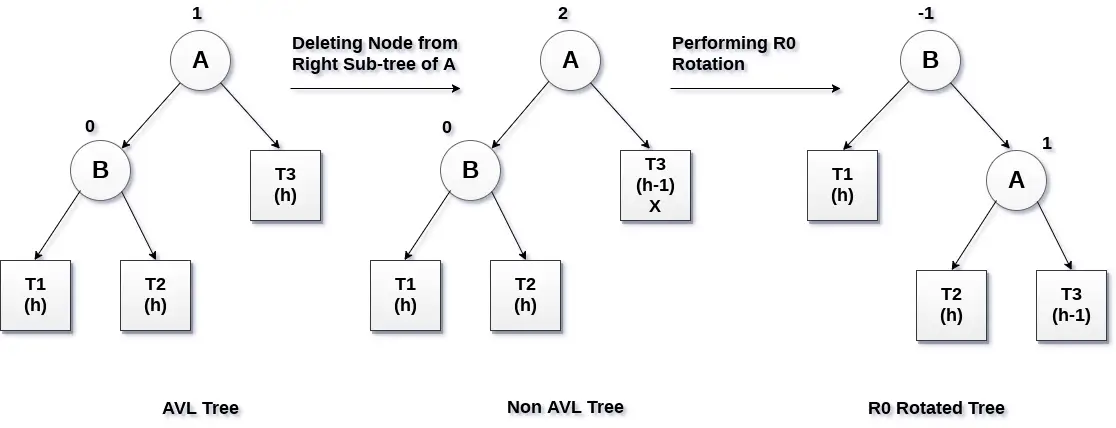
Wenn der Knoten B einen Ausgleichsfaktor von 0 hat und der Ausgleichsfaktor von Knoten A durch das Löschen des Knotens X gestört wird, wird der Baum durch Drehen des Baums mithilfe der R0-Rotation neu ausgeglichen.

Der kritische Knoten A wird nach rechts verschoben und der Knoten B wird zur Wurzel des Baums mit T1 als linkem Unterbaum. Die Teilbäume T2 und T3 werden zum linken und rechten Teilbaum des Knotens A. Der an der R0-Rotation beteiligte Prozess ist in der folgenden Abbildung dargestellt.

Beispiel:

Löschen Sie den Knoten 30 aus dem im folgenden Bild gezeigten AVL-Baum.

Lösung

In diesem Fall hat der Knoten B den Ausgleichsfaktor 0, daher wird der Baum mithilfe der R0-Rotation gedreht, wie in der folgenden Abbildung dargestellt. Der Knoten B(10) wird zur Wurzel, während der Knoten A nach rechts verschoben wird. Das rechte Kind von Knoten B wird nun zum linken Kind von Knoten A.

Java liest die Datei Zeile für Zeile

R1 Rotation (Knoten B hat Balancefaktor 1)

Die R1-Rotation muss durchgeführt werden, wenn der Ausgleichsfaktor von Knoten B 1 ist. Bei der R1-Rotation wird der kritische Knoten A nach rechts verschoben, wobei die Unterbäume T2 und T3 ihr linkes bzw. rechtes Kind sind. T1 soll als linker Teilbaum des Knotens B platziert werden.

Der Prozess der R1-Rotation ist im folgenden Bild dargestellt.

Beispiel

Löschen Sie Knoten 55 aus dem im folgenden Bild gezeigten AVL-Baum.

Lösung :

Das Löschen von 55 aus dem AVL-Baum stört den Gleichgewichtsfaktor des Knotens 50, d. h. Knoten A, der zum kritischen Knoten wird. Dies ist der Zustand der R1-Rotation, bei dem der Knoten A nach rechts verschoben wird (siehe Abbildung unten). Die rechte Seite von B ist nun die linke Seite von A (d. h. 45).

Der an der Lösung beteiligte Prozess ist in der folgenden Abbildung dargestellt.

string.replaceall in Java

R-1-Rotation (Knoten B hat Ausgleichsfaktor -1)

Die R-1-Rotation muss durchgeführt werden, wenn der Knoten B den Ausgleichsfaktor -1 hat. Dieser Fall wird wie die LR-Rotation behandelt. In diesem Fall wird der Knoten C, der das rechte Kind von Knoten B ist, zum Wurzelknoten des Baums mit B und A als seinen linken bzw. rechten Kindern.

Die Teilbäume T1, T2 werden zu den linken und rechten Teilbäumen von B, während T3, T4 zu den linken und rechten Teilbäumen von A werden.

Der Prozess der R-1-Rotation ist im folgenden Bild dargestellt.

Beispiel

Löschen Sie den Knoten 60 aus dem im folgenden Bild gezeigten AVL-Baum.

Lösung:

In diesem Fall hat Knoten B den Ausgleichsfaktor -1. Das Löschen des Knotens 60 stört den Gleichgewichtsfaktor des Knotens 50, daher muss er um R-1 gedreht werden. Der Knoten C, d. h. 45, wird zur Wurzel des Baums mit dem Knoten B(40) und A(50) als seinem linken und rechten Kind.