Einfügungssortierung und Auswahlsortierung sind zwei beliebte Sortieralgorithmen, und ihr Hauptunterschied besteht darin, wie sie Elemente auswählen und in einer sortierten Reihenfolge platzieren.
Auswahlsortierung:
- Bei der Auswahlsortierung wird das Eingabearray in zwei Teile unterteilt: einen sortierten Teil und einen unsortierten Teil.
- Der Algorithmus findet wiederholt das kleinste Element im unsortierten Teil und tauscht es mit dem Element ganz links im unsortierten Teil aus, wodurch der sortierte Teil um ein Element erweitert wird.
- Die Auswahlsortierung hat in allen Fällen eine zeitliche Komplexität von O(n^2).
Sortieren durch Einfügen:
- Bei der Einfügungssortierung wird das Eingabearray ebenfalls in zwei Teile unterteilt: einen sortierten Teil und einen unsortierten Teil.
Der Algorithmus greift ein Element aus dem unsortierten Teil auf und platziert es an der richtigen Position im sortierten Teil, wobei die größeren Elemente um eine Position nach rechts verschoben werden.
Die Einfügungssortierung hat im schlechtesten Fall eine Zeitkomplexität von O(n^2), kann jedoch bei teilweise sortierten Arrays eine bessere Leistung erbringen, wobei die Zeitkomplexität im besten Fall O(n) beträgt.
Hauptunterschiede: - Die Auswahlsortierung durchsucht den unsortierten Teil, um das minimale Element zu finden, während die Einfügungssortierung den sortierten Teil durchsucht, um die richtige Position für die Platzierung des Elements zu finden.
Die Auswahlsortierung erfordert weniger Austauschvorgänge als die Einfügesortierung, aber mehr Vergleiche.
Die Einfügungssortierung ist effizienter als die Auswahlsortierung, wenn das Eingabearray teilweise oder fast sortiert ist, während die Auswahlsortierung eine bessere Leistung erbringt, wenn das Array stark unsortiert ist.
Zusammenfassend lässt sich sagen, dass beide Algorithmen eine ähnliche zeitliche Komplexität aufweisen, ihre Auswahl- und Platzierungsmethoden jedoch unterschiedlich sind. Die Wahl zwischen ihnen hängt von den Eigenschaften der Eingabedaten und den spezifischen Anforderungen des jeweiligen Problems ab.
Vorteile der Einfügungssortierung:
- Einfach und leicht zu verstehen und umzusetzen.
- Effizient für kleine Datensätze oder nahezu sortierte Daten.
- In-Place-Sortieralgorithmus, was bedeutet, dass kein zusätzlicher Speicher erforderlich ist.
- Stabiler Sortieralgorithmus, d. h. er behält die relative Reihenfolge gleicher Elemente im Eingabearray bei.
Nachteile der Einfügungssortierung:
- Ineffizient für große Datensätze oder umgekehrt geordnete Daten, mit einer Zeitkomplexität im ungünstigsten Fall von O(n^2).
- Die Einfügungssortierung weist viele Swaps auf, was sie auf modernen Computern langsam machen kann.
Vorteile der Auswahlsortierung:
- Einfach und leicht zu verstehen und umzusetzen.
- Effizient für kleine Datensätze oder nahezu sortierte Daten.
- In-Place-Sortieralgorithmus, was bedeutet, dass kein zusätzlicher Speicher erforderlich ist.
Nachteile der Auswahlsortierung:
- Ineffizient für große Datensätze, mit einer Zeitkomplexität im ungünstigsten Fall von O(n^2).
- Die Auswahlsortierung weist viele Vergleiche auf, was sie auf modernen Computern langsam machen kann.
- Instabiler Sortieralgorithmus, was bedeutet, dass die relative Reihenfolge gleicher Elemente im Eingabearray möglicherweise nicht beibehalten wird.
In diesem Artikel besprechen wir den Unterschied zwischen der Einfügesortierung und der Auswahlsortierung:
Sortieren durch Einfügen ist ein einfacher Sortieralgorithmus, der ähnlich funktioniert wie die Art und Weise, wie Sie Spielkarten in Ihren Händen sortieren. Das Array ist quasi in einen sortierten und einen unsortierten Teil aufgeteilt. Werte aus dem unsortierten Teil werden ausgewählt und an der richtigen Position im sortierten Teil platziert.
Algorithmus:
So sortieren Sie ein Array der Größe n in aufsteigender Reihenfolge:
- Iterieren Sie von arr[1] zu arr[n] über das Array.
- Vergleichen Sie das aktuelle Element (Schlüssel) mit seinem Vorgänger.
- Wenn das Schlüsselelement kleiner als sein Vorgänger ist, vergleichen Sie es mit den vorherigen Elementen. Verschieben Sie die größeren Elemente um eine Position nach oben, um Platz für das ausgetauschte Element zu schaffen.
Unten sehen Sie das Bild zur Veranschaulichung der Einfügungssortierung:
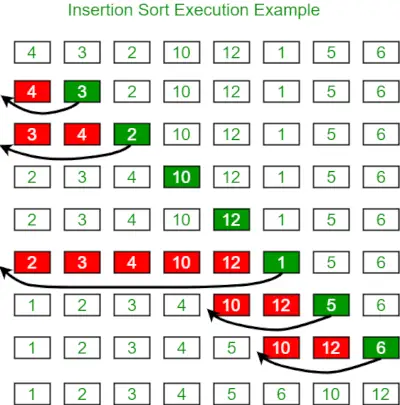
Nachfolgend finden Sie das entsprechende Programm:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j – 1; } arr[j + 1] = key; } } // Funktion zum Drucken eines Arrays der Größe N void printArray(int arr[], int n) { int i; // Das Array ausgeben für (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j – 1; } arr[j + 1] = key; } } // Funktion zum Drucken eines Arrays der Größe N static void printArray(int arr[], int n) { int i; // Das Array ausgeben für (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Treibercode public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; // Funktionsaufruf insert(arr, N); Dieser Code wurde von code_hunt bereitgestellt |
>
# Python 3 program for the insertion sort># Function to sort an array using># insertion sort>def>insertionSort(arr, n):>>i>=>0>>key>=>0>>j>=>0>>for>i>in>range>(>1>,n,>1>):>>key>=>arr[i]>>j>=>i>->1>># Move elements of arr[0..i-1],>># that are greater than key to>># one position ahead of their>># current position>>while>(j>>=>0>and>arr[j]>Schlüssel):>>arr[j>+>1>]>=>arr[j]>>j>=>j>->1>>arr[j>+>1>]>=>key># Function to print an array of size N>def>printArray(arr, n):>>i>=>0>># Print the array>>for>i>in>range>(n):>>print>(arr[i],end>=>' '>)>>print>(>' '>,end>=>'')># Driver Code>if>__name__>=>=>'__main__'>:>>arr>=>[>12>,>11>,>13>,>5>,>6>]>>N>=>len>(arr)>># Function Call>>insertionSort(arr, N)>>printArray(arr, N)>>># This code is contributed by bgangwar59.>>>C#
// C# program for the above approach>using>System;>class>GFG>{>>// Function to sort an array using>>// insertion sort>>static>void>insertionSort(>int>[] arr,>int>n)>>{>>int>i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j – 1; } arr[j + 1] = key; } } // Funktion zum Drucken eines Arrays der Größe N static void printArray(int[] arr, int n) { int i; // Das Array ausgeben für (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Treibercode static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; // Funktionsaufruf insert(arr, N); printArray(arr, N); beigetragen von Dharanendra LV>>>Javascript
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> key) { arr[j + 1] = arr[j]; j = j – 1; } arr[j + 1] = key; } } // Funktion zum Drucken eines Arrays der Größe N function printArray(arr,n) { let i; // Array drucken for (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Treibercode let arr=[12, 11 , 13, 5, 6]; let N = arr.length; // Funktionsaufruf insert(arr, N); // Dieser Code wird von avanitrachhadiya2155 beigesteuert;>5 6 11 12 13> Der Auswahl sortieren Der Algorithmus sortiert ein Array, indem er wiederholt das kleinste Element (in aufsteigender Reihenfolge) aus dem unsortierten Teil findet und es an den Anfang setzt. Der Algorithmus verwaltet zwei Unterarrays in einem bestimmten Array.
- Das Subarray ist bereits sortiert.
- Das verbleibende Subarray ist unsortiert.
Bei jeder Iteration der Auswahlsortierung wird das minimale Element (in aufsteigender Reihenfolge) aus dem unsortierten Subarray ausgewählt und in das sortierte Subarray verschoben.
Nachfolgend finden Sie ein Beispiel zur Erläuterung der oben genannten Schritte:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>Nachfolgend finden Sie das entsprechende Programm:
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>Java
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
So initialisieren Sie ein Array in Java
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>Javascript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>Ausgabe:Sorted array: 11 12 22 25 64>Tabellarischer Unterschied zwischen Einfügungssortierung und Auswahlsortierung:
Sortieren durch Einfügen Auswahlsortierung 1. Fügt den Wert in das vorsortierte Array ein, um die Wertemenge im Array zu sortieren. Sucht die minimale/maximale Anzahl aus der Liste und sortiert sie in aufsteigender/absteigender Reihenfolge. 2. Es handelt sich um einen stabilen Sortieralgorithmus. Es handelt sich um einen instabilen Sortieralgorithmus. 3. Die Zeitkomplexität beträgt im besten Fall Ω(N), wenn das Array bereits in aufsteigender Reihenfolge vorliegt. Es hat Θ(N2) im schlimmsten Fall und im durchschnittlichen Fall. Für den besten Fall, den schlechtesten Fall und die durchschnittliche Auswahlsortierung beträgt die Komplexität Θ(N2). 4. Die Anzahl der in diesem Sortieralgorithmus durchgeführten Vergleichsoperationen ist geringer als die durchgeführte Vertauschung. Die Anzahl der in diesem Sortieralgorithmus durchgeführten Vergleichsoperationen ist größer als die durchgeführte Vertauschung. 5. Es ist effizienter als die Auswahlsortierung. Es ist weniger effizient als die Einfügungssortierung. 6. Hier ist das Element im Voraus bekannt und wir suchen nach der richtigen Position, um es zu platzieren. Der Ort, an dem das Element platziert werden soll, ist bereits bekannt. Wir suchen nach dem Element, das an dieser Position eingefügt werden soll. 7. Die Einfügungssortierung wird verwendet, wenn:
- Das Array besteht aus einer kleinen Anzahl von Elementen
- Es müssen nur noch wenige Elemente sortiert werden
Die Auswahlsortierung wird verwendet, wenn
- Eine kleine Liste soll sortiert werden
- Die Kosten für den Tausch spielen keine Rolle
- Die Überprüfung aller Elemente ist obligatorisch
- Die Kosten für das Schreiben in den Speicher sind ähnlich wie im Flash-Speicher (die Anzahl der Swaps beträgt O(n) im Vergleich zu O(n2) der Blasensortierung).
8. Die Einfügungssortierung ist adaptiv, d. h. effizient für Datensätze, die bereits im Wesentlichen sortiert sind: Die zeitliche Komplexität beträgt O(kn) wenn jedes Element in der Eingabe nicht mehr als ist k Orte entfernt von seiner sortierten Position Die Auswahlsortierung ist ein Sortieralgorithmus für den direkten Vergleich
