Der euklidische Algorithmus ist eine Möglichkeit, den größten gemeinsamen Teiler zweier positiver Ganzzahlen zu ermitteln. Der GCD zweier Zahlen ist die größte Zahl, die beide teilt. Eine einfache Möglichkeit, den GCD zu ermitteln, besteht darin, beide Zahlen zu faktorisieren und gemeinsame Primfaktoren zu multiplizieren.
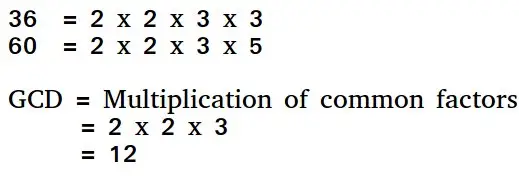
Grundlegender euklidischer Algorithmus für GCD:
Der Algorithmus basiert auf den folgenden Fakten.
- Wenn wir eine kleinere Zahl von einer größeren subtrahieren (wir reduzieren eine größere Zahl), ändert sich der GCD nicht. Wenn wir also immer wieder den größeren von zwei subtrahieren, erhalten wir GCD.
- Wenn wir nun anstelle einer Subtraktion die kleinere Zahl dividieren, stoppt der Algorithmus, wenn wir den Rest 0 finden.
Nachfolgend finden Sie eine rekursive Funktion zur Auswertung von gcd mithilfe des Euklid-Algorithmus:
C
// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 35, b = 10;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 31, b = 2;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >return> 0;> }> |
>
>
CPP
// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 35, b = 10;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 31, b = 2;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >return> 0;> }> |
>
vergleiche mit Java
>
Java
// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a ==>0>)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver code> >public> static> void> main(String[] args)> >{> >int> a =>10>, b =>15>, g;> > >// Function call> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>35>;> >b =>10>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>31>;> >b =>2>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // Code Contributed by Mohit Gupta_OMG> |
>
>
Python3
# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> >if> a>=>=> 0>:> >return> b> >return> gcd(b>%> a, a)> # Driver code> if> __name__>=>=> '__main__'>:> >a>=> 10> >b>=> 15> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 35> >b>=> 10> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 31> >b>=> 2> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> # Code Contributed By Mohit Gupta_OMG> |
>
>
C#
// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver Code> >static> public> void> Main()> >{> >int> a = 10, b = 15, g;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 35;> >b = 10;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 31;> >b = 2;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // This code is contributed by ajit> |
>
>
PHP
String-Methoden in Java
// php program to demonstrate Basic Euclidean Algorithm> // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) { if ($a == 0) return $b; return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ', gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ', gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ', gcd($a, $b); // This code is contributed by m_kit ?>> |
>
>
Javascript
// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> >let a = 10, b = 15;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 35, b = 10;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 31, b = 2;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> // This code contributed by aashish1995> |
>
>Ausgabe
GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1>
Zeitkomplexität: O(Log min(a, b))
Hilfsraum: O(Log (min(a,b))
Erweiterter euklidischer Algorithmus:
Der erweiterte euklidische Algorithmus findet auch ganzzahlige Koeffizienten x und y, so dass: ax + by = ggT(a, b)
Beispiele:
Eingang: a = 30, b = 20
Ausgabe: gcd = 10, x = 1, y = -1
(Beachten Sie, dass 30*1 + 20*(-1) = 10)Eingang: a = 35, b = 15
Ausgabe: gcd = 5, x = 1, y = -2
(Beachten Sie, dass 35*1 + 15*(-2) = 5)
Der erweiterte euklidische Algorithmus aktualisiert die Ergebnisse von gcd(a, b) mithilfe der Ergebnisse, die durch den rekursiven Aufruf gcd(b%a, a) berechnet wurden. Die durch den rekursiven Aufruf berechneten Werte von x und y seien x1Andy1. x und y werden mit den folgenden Ausdrücken aktualisiert.
Empfohlene Praxis Erweiterter euklidischer Algorithmus Probieren Sie es aus!ax + by = ggT(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x1+ ist1
ax + by = (b%a)x1+ ist1
ax + by = (b – [b/a] * a)x1+ ist1
ax + by = a(y1– [b/a] * x1) + bx1Vergleich von LHS und RHS,
x = y1– ?b/a? * X1
y = x1
Nachfolgend finden Sie eine Implementierung des oben genannten Ansatzes:
C++
// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of> >// recursive call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Code> int> main()> {> >int> x, y, a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >cout <<>'GCD('> << a <<>', '> << b> ><<>') = '> << g << endl;> >return> 0;> }> |
>
>
C
// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of recursive> >// call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Program> int> main()> {> >int> x, y;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >printf>(>'gcd(%d, %d) = %d'>, a, b, g);> >return> 0;> }> |
>
>
Java
// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,>int> x,> >int> y)> >{> >// Base Case> >if> (a ==>0>) {> >x =>0>;> >y =>1>;> >return> b;> >}> >int> x1 =>1>,> >y1 =>1>;>// To store results of recursive call> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using results of recursive> >// call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> >// Driver Program> >public> static> void> main(String[] args)> >{> >int> x =>1>, y =>1>;> >int> a =>35>, b =>15>;> >int> g = gcdExtended(a, b, x, y);> >System.out.print(>'gcd('> + a +>' , '> + b> >+>') = '> + g);> >}> }> |
>
>
Python3
# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> ># Base Case> >if> a>=>=> 0>:> >return> b,>0>,>1> >gcd, x1, y1>=> gcdExtended(b>%> a, a)> ># Update x and y using results of recursive> ># call> >x>=> y1>-> (b>/>/>a)>*> x1> >y>=> x1> >return> gcd, x, y> # Driver code> a, b>=> 35>,>15> g, x, y>=> gcdExtended(a, b)> print>(>'gcd('>, a,>','>, b,>') = '>, g)> |
Zentrieren von Bildern in CSS
>
>
C#
// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,> >int> x,>int> y)> >{> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results of> >// recursive call> >int> x1 = 1, y1 = 1;> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using> >// results of recursive call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> > >// Driver Code> >static> public> void> Main ()> >{> >int> x = 1, y = 1;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, x, y);> >Console.WriteLine(>'gcd('> + a +>' , '> +> >b +>') = '> + g);> >}> }> |
>
>
PHP
// PHP program to demonstrate // working of extended // Euclidean Algorithm // PHP function for // extended Euclidean // Algorithm function gcdExtended($a, $b, $x, $y) { // Base Case if ($a == 0) { $x = 0; $y = 1; return $b; } // To store results // of recursive call $gcd = gcdExtended($b % $a, $a, $x, $y); // Update x and y using // results of recursive // call $x = $y - floor($b / $a) * $x; $y = $x; return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>> |
>
>
Javascript
> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> >x, y)> {> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results> >// of recursive call> >let gcd = gcdExtended(b % a,> >a, x, y);> >// Update x and y using> >// results of recursive> >// call> >x = y - (b / a) * x;> >y = x;> >return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(>'gcd('> + a);> document.write(>', '> + b +>')'>);> document.write(>' = '> + g);> > |
>
>
Ausgabe :
gcd(35, 15) = 5>
Zeitkomplexität: O(log N)
Hilfsraum: O(log N)
Wie funktioniert der erweiterte Algorithmus?
Wie oben gesehen, sind x und y Ergebnisse für die Eingaben a und b.
a.x + b.y = gcd —-(1)
Und x1Andy1sind Ergebnisse für die Eingaben b%a und a
(b%a).x1+ a.y1= gcd
Wenn wir oben b%a = (b – (?b/a?).a) einsetzen,
wir folgen. Beachten Sie, dass ?b/a? ist Boden(b/a)(b – (?b/a?).a).x1+ a.y1= gcd
Die obige Gleichung kann auch wie folgt geschrieben werden
b.x1+ a.(und1– (?b/a?).x1) = gcd —(2)
Nach dem Vergleich der Koeffizienten von „a“ und „b“ in (1) und
(2) Wir erhalten Folgendes:
x = y1– ?b/a? * X1
y = x1
Wie ist der erweiterte Algorithmus nützlich?
Der erweiterte euklidische Algorithmus ist besonders nützlich, wenn a und b teilerfremd sind (oder ggT 1 ist). Da x die modulare multiplikative Umkehrung von a modulo b ist und y die modulare multiplikative Umkehrung von b modulo a ist. Insbesondere die Berechnung der modularen multiplikativen Umkehrung ist ein wesentlicher Schritt in der RSA-Verschlüsselungsmethode mit öffentlichem Schlüssel.
