Gegeben sei eine rechteckige Matrix mat[][] Wenn einige Zellen Landminen enthalten (gekennzeichnet mit 0) und der Rest sicher ist (gekennzeichnet mit 1), ermitteln Sie die Länge des kürzesten sicheren Weges von einer beliebigen Zelle in der ersten Spalte zu einer beliebigen Zelle in der letzten Spalte.
- Landminen sind unsicher und ihre vier angrenzenden Felder (oben unten links rechts) sind ebenfalls unsicher.
- Es sind nur horizontale und vertikale Bewegungen zu benachbarten sicheren Zellen zulässig.
- Wenn es unmöglich ist, die letzte Spalte sicher zu erreichen, geben Sie -1 zurück.
Beispiele:
Eingang:
with[][] = [ [1 0 1 1 1]
[1 1 1 1 1]
[1 1 1 1 1]
[1 1 1 0 1]
[1 1 1 1 0] ]
Ausgabe: 6
Erläuterung:
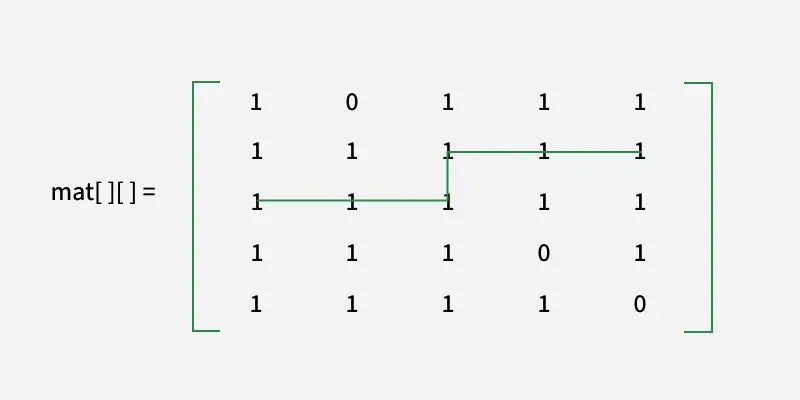
Wir können sehen, dass die Länge die kürzeste ist
Der sichere Weg ist 6.
Eingang:
mit[][] = [ [1 1 1 1 1]
[1 1 0 1 1]
[1 1 1 1 1] ]
Ausgabe: -1
Erläuterung: Es gibt keinen möglichen Weg von dort
erste Spalte bis letzte Spalte.
Inhaltsverzeichnis
[Ansatz] Backtracking verwenden
C++Die Idee ist zu verwenden Zurückverfolgen . Wir markieren zunächst alle angrenzenden Zellen der Landminen als unsicher. Dann bewegen wir uns für jede sichere Zelle der ersten Spalte der Matrix in alle zulässigen Richtungen vorwärts und prüfen rekursiv, ob sie zum Ziel führt oder nicht. Wenn das Ziel gefunden wird, aktualisieren wir den Wert des kürzesten Pfads. Wenn keine der oben genannten Lösungen funktioniert, geben wir von unserer Funktion „Falsch“ zurück.
#include
import java.util.Arrays; class Solution { // Function to mark unsafe cells (landmines and their adjacent cells) private void markUnsafeCells(int[][] mat) { int r = mat.length; int c = mat[0].length; int[] row = {-1 1 0 0}; int[] col = {0 0 -1 1}; // Create a copy to avoid modifying original safe cells prematurely int[][] temp = new int[r][c]; for (int i = 0; i < r; i++) { for (int j = 0; j < c; j++) { temp[i][j] = mat[i][j]; } } // Mark adjacent cells of landmines (0) as unsafe (0) for (int i = 0; i < r; i++) { for (int j = 0; j < c; j++) { if (temp[i][j] == 0) { for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; if (ni >= 0 && ni < r && nj >= 0 && nj < c) { mat[ni][nj] = 0; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int dfs(int[][] mat boolean[][] visited int i int j int c) { int r = mat.length; // If out of bounds blocked or visited if (i < 0 || i >= r || j < 0 || j >= c || mat[i][j] == 0 || visited[i][j]) { return Integer.MAX_VALUE; } if (j == c - 1) { return 1; } visited[i][j] = true; int[] row = {-1 1 0 0}; int[] col = {0 0 -1 1}; int minPath = Integer.MAX_VALUE; // Try all four directions for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; int pathLength = dfs(mat visited ni nj c); if (pathLength != Integer.MAX_VALUE) { minPath = Math.min(minPath 1 + pathLength); } } // Backtrack - unmark current cell visited[i][j] = false; return minPath; } public int findShortestPath(int[][] mat) { int r = mat.length; int c = mat[0].length; // Mark all adjacent cells of landmines as unsafe markUnsafeCells(mat); boolean[][] visited = new boolean[r][c]; int minPath = Integer.MAX_VALUE; // Try starting from each safe cell in the first column for (int i = 0; i < r; i++) { if (mat[i][0] == 1) { int pathLength = dfs(mat visited i 0 c); if (pathLength != Integer.MAX_VALUE) { minPath = Math.min(minPath pathLength); } } } return minPath == Integer.MAX_VALUE ? -1 : minPath; } public static void main(String[] args) { int[][] mat = { {1 0 1 1 1} {1 1 1 1 1} {1 1 1 1 1} {1 1 1 0 1} {1 1 1 1 0} }; Solution solution = new Solution(); int result = solution.findShortestPath(mat); System.out.println(result); } }
# Function to mark unsafe cells (landmines and their adjacent cells) def mark_unsafe_cells(mat): r = len(mat) c = len(mat[0]) # Directions for adjacent cells: up down left right row = [-1 1 0 0] col = [0 0 -1 1] # Create a copy to avoid modifying original safe cells prematurely temp = [row[:] for row in mat] # Mark adjacent cells of landmines (0) as unsafe (0) for i in range(r): for j in range(c): if temp[i][j] == 0: for k in range(4): ni = i + row[k] nj = j + col[k] if 0 <= ni < r and 0 <= nj < c: mat[ni][nj] = 0 # DFS to find shortest path from (i j) to any cell in last column def dfs(mat visited i j c): r = len(mat) # If out of bounds blocked or visited if i < 0 or i >= r or j < 0 or j >= c or mat[i][j] == 0 or visited[i][j]: return float('inf') if j == c - 1: return 1 visited[i][j] = True # Four possible moves: up down left right row = [-1 1 0 0] col = [0 0 -1 1] min_path = float('inf') # Try all four directions for k in range(4): ni = i + row[k] nj = j + col[k] path_length = dfs(mat visited ni nj c) if path_length != float('inf'): min_path = min(min_path 1 + path_length) # Backtrack - unmark current cell visited[i][j] = False return min_path def findShortestPath(mat): r = len(mat) c = len(mat[0]) # Mark all adjacent cells of landmines as unsafe mark_unsafe_cells(mat) visited = [[False] * c for _ in range(r)] min_path = float('inf') # Try starting from each safe cell in the first column for i in range(r): if mat[i][0] == 1: path_length = dfs(mat visited i 0 c) if path_length != float('inf'): min_path = min(min_path path_length) return -1 if min_path == float('inf') else min_path def main(): mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ] result = findShortestPath(mat) print(result) if __name__ == '__main__': main()
using System; class GFG { // Function to mark unsafe cells (landmines and their adjacent cells) private void MarkUnsafeCells(int[][] mat) { int r = mat.Length; int c = mat[0].Length; // Directions for adjacent cells: up down left right int[] row = { -1 1 0 0 }; int[] col = { 0 0 -1 1 }; // Create a copy to avoid modifying original safe cells prematurely int[][] temp = new int[r][]; for (int i = 0; i < r; i++) { temp[i] = new int[c]; Array.Copy(mat[i] temp[i] c); } // Mark adjacent cells of landmines (0) as unsafe (0) for (int i = 0; i < r; i++) { for (int j = 0; j < c; j++) { if (temp[i][j] == 0) { for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; if (ni >= 0 && ni < r && nj >= 0 && nj < c) { mat[ni][nj] = 0; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int Dfs(int[][] mat bool[][] visited int i int j int c) { int r = mat.Length; // If out of bounds blocked or visited if (i < 0 || i >= r || j < 0 || j >= c || mat[i][j] == 0 || visited[i][j]) { return int.MaxValue; } if (j == c - 1) { return 1; } visited[i][j] = true; int[] row = { -1 1 0 0 }; int[] col = { 0 0 -1 1 }; int minPath = int.MaxValue; // Try all four directions for (int k = 0; k < 4; k++) { int ni = i + row[k]; int nj = j + col[k]; int pathLength = Dfs(mat visited ni nj c); if (pathLength != int.MaxValue) { minPath = Math.Min(minPath 1 + pathLength); } } // Backtrack - unmark current cell visited[i][j] = false; return minPath; } public int FindShortestPath(int[][] mat) { int r = mat.Length; int c = mat[0].Length; // Mark all adjacent cells of landmines as unsafe MarkUnsafeCells(mat); bool[][] visited = new bool[r][]; for (int i = 0; i < r; i++) { visited[i] = new bool[c]; } int minPath = int.MaxValue; // Try starting from each safe cell in the first column for (int i = 0; i < r; i++) { if (mat[i][0] == 1) { int pathLength = Dfs(mat visited i 0 c); if (pathLength != int.MaxValue) { minPath = Math.Min(minPath pathLength); } } } return minPath == int.MaxValue ? -1 : minPath; } static void Main(string[] args) { int[][] mat = new int[][] { new int[] { 1 0 1 1 1 } new int[] { 1 1 1 1 1 } new int[] { 1 1 1 1 1 } new int[] { 1 1 1 0 1 } new int[] { 1 1 1 1 0 } }; GFG solution = new GFG(); int result = solution.FindShortestPath(mat); Console.WriteLine(result); } }
function markUnsafeCells(mat) { const r = mat.length; const c = mat[0].length; // Directions for adjacent cells: up down left right const row = [-1 1 0 0]; const col = [0 0 -1 1]; // Create a copy to avoid modifying original safe cells prematurely const temp = mat.map(row => [...row]); // Mark adjacent cells of landmines (0) as unsafe (0) for (let i = 0; i < r; i++) { for (let j = 0; j < c; j++) { if (temp[i][j] === 0) { for (let k = 0; k < 4; k++) { const ni = i + row[k]; const nj = j + col[k]; if (ni >= 0 && ni < r && nj >= 0 && nj < c) { mat[ni][nj] = 0; } } } } } } function dfs(mat visited i j c) { const r = mat.length; // If out of bounds blocked or visited if (i < 0 || i >= r || j < 0 || j >= c || mat[i][j] === 0 || visited[i][j]) { return Infinity; } // If reached the last column if (j === c - 1) { return 1; } visited[i][j] = true; const row = [-1 1 0 0]; const col = [0 0 -1 1]; let minPath = Infinity; // Try all four directions for (let k = 0; k < 4; k++) { const ni = i + row[k]; const nj = j + col[k]; const pathLength = dfs(mat visited ni nj c); if (pathLength !== Infinity) { minPath = Math.min(minPath 1 + pathLength); } } // Backtrack - unmark current cell visited[i][j] = false; return minPath; } function findShortestPath(mat) { const r = mat.length; const c = mat[0].length; // Mark all adjacent cells of landmines as unsafe markUnsafeCells(mat); const visited = Array(r).fill().map(() => Array(c).fill(false)); let minPath = Infinity; // Try starting from each safe cell in the first column for (let i = 0; i < r; i++) { if (mat[i][0] === 1) { const pathLength = dfs(mat visited i 0 c); if (pathLength !== Infinity) { minPath = Math.min(minPath pathLength); } } } return minPath === Infinity ? -1 : minPath; } const mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ]; const result = findShortestPath(mat); console.log(result);
Ausgabe
6
Zeitkomplexität: O(4^(r * c)) wobei r die Anzahl der Zeilen und c die Anzahl der Spalten in der angegebenen Matrix ist.
Hilfsraum: O(r * c) da wir zusätzlichen Platz wie visted[r][c] verwenden.
Endlosschleife
[Optimierter Ansatz] Verwendung der Breitensuche
C++Es kann mithilfe der Breitensuche in polynomieller Zeit gelöst werden. Alle sicheren Zellen aus der letzten Spalte in die Warteschlange mit Abstand = 1 einreihen. Während BFS fortfährt, wird der kürzeste Pfad zu jeder Zelle aus der letzten Spalte berechnet. Schließlich wird unter allen erreichbaren Zellen in der ersten Spalte der Mindestabstand ausgegeben.
#include
import java.util.*; public class Solution { static int[] rowNum = {-1 0 0 1}; static int[] colNum = {0 -1 1 0}; public static int findShortestPath(int[][] mat) { int n = mat.length; int m = mat[0].length; Queue<int[]> q = new LinkedList<>(); int[][] d = new int[n][m]; // Initializing distance array with large values for (int i = 0; i < n; i++) { Arrays.fill(d[i] (int) 1e9); } // Lambda-like helper function: check if cell is valid java.util.function.BiFunction<Integer Integer Boolean> isValid = (i j) -> { return !(i < 0 || i >= n || j < 0 || j >= m); }; // Helper function: check if cell and adjacent cells are safe java.util.function.BiFunction<Integer Integer Boolean> check = (i j) -> { if (!isValid.apply(i j)) return false; for (int k = 0; k < 4; k++) { int ni = i + rowNum[k]; int nj = j + colNum[k]; if (isValid.apply(ni nj) && mat[ni][nj] == 0) return false; } return true; }; // Pushing cells from the rightmost column into the queue for (int i = 0; i < n; i++) { if (check.apply(i m - 1)) { q.add(new int[]{i m - 1 1}); } } // BFS traversal while (!q.isEmpty()) { int[] z = q.poll(); int x = z[0] y = z[1] dis = z[2]; if (d[x][y] > dis) { d[x][y] = dis; for (int k = 0; k < 4; k++) { int ni = x + rowNum[k]; int nj = y + colNum[k]; if (check.apply(ni nj)) { q.add(new int[]{ni nj dis + 1}); } } } } // Finding the minimum distance in the first column int ans = (int) 1e9; for (int i = 0; i < n; i++) { ans = Math.min(ans d[i][0]); } // If no safe path found return -1 if (ans >= 1e9) ans = -1; return ans; } public static void main(String[] args) { int[][] mat = { {1 0 1 1 1} {1 1 1 1 1} {1 1 1 1 1} {1 1 1 0 1} {1 1 1 1 0} }; int result = findShortestPath(mat); System.out.println(result); } }
from collections import deque rowNum = [-1 0 0 1] colNum = [0 -1 1 0] def findShortestPath(mat): n = len(mat) m = len(mat[0]) q = deque() d = [[10**9 for _ in range(m)] for _ in range(n)] # Check if cell is valid def isValid(i j): return not (i < 0 or i >= n or j < 0 or j >= m) # Check if cell and its adjacent cells are safe def check(i j): if not isValid(i j): return False for k in range(4): ni nj = i + rowNum[k] j + colNum[k] if isValid(ni nj) and mat[ni][nj] == 0: return False return True # Pushing cells from the rightmost column into the queue for i in range(n): if check(i m - 1): q.append((i m - 1 1)) # BFS traversal while q: x y dis = q.popleft() if d[x][y] > dis: d[x][y] = dis for k in range(4): ni nj = x + rowNum[k] y + colNum[k] if check(ni nj): q.append((ni nj dis + 1)) # Finding the minimum distance in the first column ans = min(d[i][0] for i in range(n)) # If no safe path found return -1 if ans >= 10**9: ans = -1 return ans if __name__ == '__main__': mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ] result = findShortestPath(mat) print(result)
using System; using System.Collections.Generic; class Solution { static int[] rowNum = { -1 0 0 1 }; static int[] colNum = { 0 -1 1 0 }; // Check if cell is valid static bool IsValid(int i int j int n int m) { return !(i < 0 || i >= n || j < 0 || j >= m); } // Check if cell and its adjacent cells are safe static bool Check(int i int j int[][] mat int n int m) { if (!IsValid(i j n m)) return false; for (int k = 0; k < 4; k++) { int ni = i + rowNum[k]; int nj = j + colNum[k]; if (IsValid(ni nj n m) && mat[ni][nj] == 0) return false; } return true; } public static int FindShortestPath(int[][] mat) { int n = mat.Length; int m = mat[0].Length; Queue<(int int int)> q = new Queue<(int int int)>(); int[] d = new int[n m]; // Initialize distance array with large value for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) d[i j] = int.MaxValue / 2; // Push safe cells from rightmost column for (int i = 0; i < n; i++) { if (Check(i m - 1 mat n m)) { q.Enqueue((i m - 1 1)); } } // BFS traversal while (q.Count > 0) { var (x y dis) = q.Dequeue(); if (d[x y] > dis) { d[x y] = dis; for (int k = 0; k < 4; k++) { int ni = x + rowNum[k]; int nj = y + colNum[k]; if (Check(ni nj mat n m)) { q.Enqueue((ni nj dis + 1)); } } } } // Find minimum distance in the first column int ans = int.MaxValue / 2; for (int i = 0; i < n; i++) ans = Math.Min(ans d[i 0]); return ans >= int.MaxValue / 2 ? -1 : ans; } static void Main() { int[][] mat = new int[][] { new int[] {1 0 1 1 1} new int[] {1 1 1 1 1} new int[] {1 1 1 1 1} new int[] {1 1 1 0 1} new int[] {1 1 1 1 0} }; int result = FindShortestPath(mat); Console.WriteLine(result); } }
function findShortestPath(mat) { const n = mat.length; const m = mat[0].length; const rowNum = [-1 0 0 1]; const colNum = [0 -1 1 0]; // Distance matrix initialized to large value const d = Array.from({ length: n } () => Array(m).fill(Number.MAX_SAFE_INTEGER)); // Check if cell is valid function isValid(i j) { return !(i < 0 || i >= n || j < 0 || j >= m); } // Check if cell and its adjacent cells are safe function check(i j) { if (!isValid(i j)) return false; for (let k = 0; k < 4; k++) { let ni = i + rowNum[k]; let nj = j + colNum[k]; if (isValid(ni nj) && mat[ni][nj] === 0) return false; } return true; } // Queue for BFS let q = []; // Push safe cells from rightmost column for (let i = 0; i < n; i++) { if (check(i m - 1)) { q.push([i m - 1 1]); } } // BFS traversal while (q.length > 0) { let [x y dis] = q.shift(); if (d[x][y] > dis) { d[x][y] = dis; for (let k = 0; k < 4; k++) { let ni = x + rowNum[k]; let nj = y + colNum[k]; if (check(ni nj)) { q.push([ni nj dis + 1]); } } } } // Find minimum distance in first column let ans = Number.MAX_SAFE_INTEGER; for (let i = 0; i < n; i++) { ans = Math.min(ans d[i][0]); } return ans >= Number.MAX_SAFE_INTEGER ? -1 : ans; } const mat = [ [1 0 1 1 1] [1 1 1 1 1] [1 1 1 1 1] [1 1 1 0 1] [1 1 1 1 0] ]; const result = findShortestPath(mat); console.log(result);
Ausgabe
6
Zeitkomplexität: O(r * c) wobei r und c die Anzahl der Zeilen bzw. Spalten in der angegebenen Matrix sind.
Hilfsraum: O(r * c)
