Mit der Formel „Höhe eines Parallelogramms“ wird die Höhe eines Parallelogramms berechnet. Die Höhe eines Parallelogramms ist der senkrechte Abstand zwischen der Basisseite und der ihr gegenüberliegenden parallelen Seite. Ein Parallelogramm kann als Viereck definiert werden, bei dem gegenüberliegende Seiten parallel sind und die Länge dieser gegenüberliegenden Seiten ebenfalls gleich ist.
Höhe einer Parallelogrammformel
Die entgegengesetzten Winkel des Parallelogramms sind ebenfalls gleich. Erfahren Sie weiter unten mehr über die Formel „Höhe eines Parallelogramms“ mit Ableitung im Detail.
Höhe einer Parallelogrammformel
Höhe einer Parallelogrammformel
Die Höhe eines Parallelogramms wird mithilfe der Formel „Fläche ist gleich der Basis multipliziert mit der Höhe“ berechnet. Wenn also die Fläche von a Parallelogramm Ist bekannt, wird seine Höhe berechnet, indem man die Fläche durch seine Grundfläche dividiert.
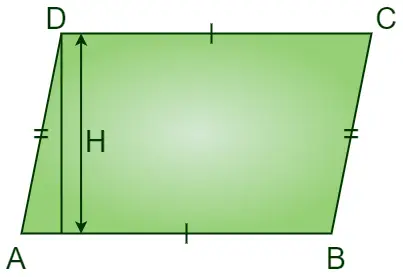
Die Höhe einer Parallelogrammformel wird aus der Flächenformel abgeleitet. Fläche eines Parallelogramms kann mithilfe der Basislänge und -höhe des Parallelogramms ermittelt werden.
Fläche = Basis × Höhe
Höhe = Fläche/Basis
Umfang eines Parallelogramms
Umfang ist definiert als die Summe aller Seiten, aus denen eine geschlossene Figur konstruiert wird. Im Fall eines Parallelogramms hat es vier Seiten, von denen die gegenüberliegenden Seiten gleich sind, sodass der Umfang die Summe aller vier Seiten ist.
Nehmen wir daher das Maß der gegenüberliegenden Seiten als X und Y
Umfang des Parallelogramms = X + Y + X + Y = 2X + 2Y = 2(X + Y)
Umfang = 2(X + Y)
Ähnliche Resourcen
- Parallele Linien
- Fläche des Rechtecks
- Umfang des Rechtecks
Gelöstes Beispiel zur Höhe des Parallelogramms
Beispiel 1: Ermitteln Sie die Höhe eines Parallelogramms, wenn seine Fläche 625 cm beträgt 2 und die Länge der Basis beträgt 25 cm.
Lösung:
Die Höhe eines Parallelogramms kann mithilfe der Formel für die Höhe eines Parallelogramms berechnet werden
Höhe = Fläche/Basis
Höhe = 625/25
Höhe = 25 cm.
Daher beträgt die Höhe des Parallelogramms 25 cm
Beispiel 2: Ermitteln Sie die Fläche eines Parallelogramms mit einer Grundfläche von 20 cm und einer Höhe von 15 cm.
Lösung:
Fläche des Parallelogramms = Basis × Höhe
Grundfläche und Höhe werden mit 20 cm bzw. 15 cm angegeben.
Fläche = 20 × 15
Fläche = 300 cm.
Beispiel 3: Der Umfang eines Parallelogramms beträgt 226 cm und eine Seite des Parallelogramms ist 12 cm lang. Ermitteln Sie das Maß der anderen Seite.
Lösung:
Python-Sortiertupel
Umfang des Parallelogramms = 2(X + Y)
Wobei X die Länge einer Seite und Y die Länge der anderen Seite ist, also sei X = 12 cm
226 = 2(X + Y)
2(X + Y) = 226
2(12 + Y) = 226
24 + 2Y =226
2Y = 226 – 24
2Y = 202
Y = 202/2
Y = 101 cm.
Beispiel 4: Ermitteln Sie die Höhe eines Parallelogramms, wenn seine Fläche 800 cm beträgt 2 und die Länge der Basis beträgt 40 cm.
Lösung
Die Höhe eines Parallelogramms kann mithilfe der Formel für die Höhe eines Parallelogramms berechnet werden
Höhe = Fläche/Basis
Höhe = 800/40
Höhe = 20 cm.
Daher beträgt die Höhe des Parallelogramms 20 cm
Beispiel 5: Der Umfang eines Parallelogramms beträgt 400 cm und eine Seite des Parallelogramms ist 80 cm lang. Ermitteln Sie das Maß der anderen Seite.
Lösung:
Umfang des Parallelogramms = 2(X + Y)
Wobei X die Länge einer Seite und Y die Länge der anderen Seite ist, also sei X = 80 cm
400 = 2(X + Y)
2(X + Y) = 400
2(80 + Y) = 400
160 + 2Y =400
2Y = 400 – 160
2Y = 240
Y = 120 cm.
Formel für die Höhe des Parallelogramms
Wie lautet die Formel für die Höhe des Parallelogramms?
Die Formel für die Höhe des Parallelogramms lautet Fläche(a)/Basis(b).
Was ist die Basis und Höhe eines Parallelogramms?
Bharti Jha
Basis bezieht sich auf die Länge einer Seite und Höhe ist die Länge einer Senkrechten zwischen zwei parallelen Linien.
Was ist die Höhe eines Parallelogramms?
Die Höhe eines Parallelogramms wird als senkrechter Abstand zwischen zwei parallelen Linien eines Parallelogramms bezeichnet.
Was ist die Fläche eines Parallelogramms?
Als Fläche eines Parallelogramms wird der Raum innerhalb der Grenze eines Parallelogramms bezeichnet.
