Dreiecke sind dreiseitige geschlossene Polygone, die durch den Schnittpunkt dreier Geraden entstehen. Es kommt im Alltag häufig vor. Es ist eine der Grundformen der Geometrie. Es hat drei Seiten, drei Winkel und drei Eckpunkte. Ein rechtwinkliges Dreieck ist ein Dreieck, bei dem einer der Winkel immer 90° beträgt. Satz des Pythagoras wird für rechtwinklige Dreiecke abgeleitet. Dies besagt, dass das Quadrat der Hypotenuse (der längsten Seite) gleich der Summe der Quadrate der Basis und der Senkrechten ist.

Angesichts der Länge von mindestens zwei Seiten eines rechtwinkligen Dreiecks können wir den Wert jedes Winkels des rechtwinkligen Dreiecks ermitteln. Hierzu verwenden wir verschiedene trigonometrische Funktionen wie Sinus, Cosinus, Tangens, Kotangens, Sec und Cosec. Diese helfen uns, die Winkel eines rechtwinkligen Dreiecks mit seinen Seiten in Beziehung zu setzen.

Eigenschaften

• Unter den drei Eckpunkten gibt es einen rechtwinkligen Eckpunkt
• Die dem rechtwinkligen Scheitelpunkt gegenüberliegende Seite wird als bezeichnet Hypotenuse .
• Die Länge der Seiten folgt dem Satz des Pythagoras, der besagt

Hypotenuse ² = Basis ² + Höhe ²

• Die Hypotenuse ist die längste Seite eines rechtwinkligen Dreiecks.
• Die anderen Winkel als der rechte Winkel sind spitze Winkel, da der Wert kleiner als 90 ist^Ö

Trigonometrische Funktionen

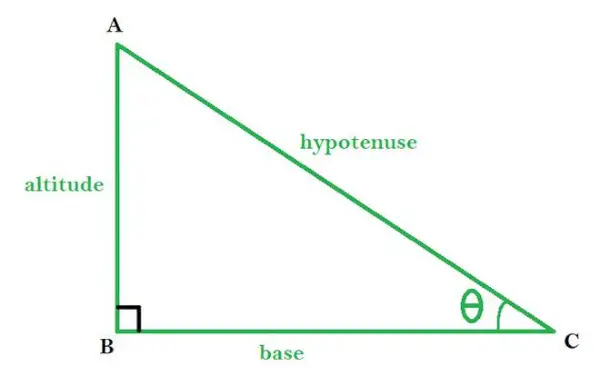
ABC ist ein rechtwinkliges Dreieck mit ∠B als rechtem Winkel

Indische Schauspielerin Rani Mukerji

• cosθ: Dies gibt das Verhältnis der Basis zur Hypotenuse eines rechtwinkligen Dreiecks an.

cosθ = Basis / Hypotenuse

• sinθ: Dies ergibt das Verhältnis der Höhe zur Hypotenuse eines rechtwinkligen Dreiecks.

sinθ = Höhe / Hypotenuse

• tanθ: Es ist das Verhältnis der Höhe zur Grundfläche eines rechtwinkligen Dreiecks.

tanθ = Höhe / Basis

• Kinderbettθ: Es ist die Umkehrung von tanθ
• Sekθ: Es ist die Umkehrung von cosθ
• cosecθ: Es ist die Umkehrung von sinθ

Um die Winkel eines rechtwinkligen Dreiecks zu ermitteln, können wir den trigonometrischen Kehrwert des Verhältnisses der gegebenen Seiten des Dreiecks ermitteln.

Beispiel:

Wenn sinθ = x, dann können wir schreiben

θ = Sünde ^-1 X.

Dies gibt den Winkel zurück, für den der Sinuswert des Winkels x ist.

Ebenso gibt es cos^-1θ, also^-1ich, Kinderbett^-1θ, Sek^-1θ und cosec^-1ich

Beispielprobleme

Frage 1. Gegeben sei ein rechtwinkliges Dreieck mit einer Basislänge von 10 cm und einer Hypotenuse von 20 cm. Ermitteln Sie den Wert des Basiswinkels.

Lösung:

Gegeben: Basis = 10 cm

Hypotenuse = 20 cm

Der Wert des Basiswinkels sei θ. Wir können schreiben

cosθ = Basis / Hypotenuse = 10/20 = 1/2

θ = cos^-1(1/2) = 60^Ö

Somit beträgt der Wert des Basiswinkels 60 ^Ö .

Frage 2: Ermitteln Sie den Wert der Winkel eines rechtwinkligen Dreiecks, vorausgesetzt, dass einer der spitzen Winkel doppelt so groß ist wie der andere.

Lösung:

Da wir wissen, dass die Summe aller drei Winkel in einem Dreieck 180 beträgt^Ö.

Da einer der Winkel 90 beträgt^Öund einer der spitzen Winkel doppelt so groß ist wie der andere, können wir sie als θ und 2θ betrachten.

So können wir schreiben

90^Ö+ θ + 2θ = 180^Ö

3θ = 180^Ö– 90^Ö

3θ = 90^Ö

θ = 90^Ö/3 = 30 ^Ö

2θ = 2 × 30^Ö= 60 ^Ö

Die Winkel betragen also 30 ^Ö , 60 ^Ö , und 90 ^Ö .

Frage 3: Ermitteln Sie den Wert des Steigungswinkels einer Leiter mit einer Länge von 5 m, vorausgesetzt, dass sich der Fuß der Leiter in einem Abstand von 3 m von der Wand befindet.

Lösung:

Da die Leiter als Hypotenuse eines rechtwinkligen Dreiecks fungiert und der Basisabstand 3 m beträgt, können wir schreiben

Hypotenuse = 5m

Basis = 3m

Der Höhenwinkel sei θ. So können wir schreiben

cosθ = Basis / Hypotenuse = 3/5

θ = cos^-1(3/5)

θ = 53^Ö

Somit beträgt der Wert des Höhenwinkels 53^Ö.

Frage 4: Ermitteln Sie den Wert der Hypotenuse unter der Annahme, dass die Länge der Höhe 8 m und der Basiswinkel 30 beträgt ^Ö .

Lösung:

Gegeben sei der Basiswinkel gleich 30°^Öund die Höhe 8 m beträgt, können wir die Sinusfunktion anwenden, um die Länge der Hypotenuse zu ermitteln.

Sünde30 ^Ö = Höhe / Hypotenuse

Hypotenuse = Höhe / sin30^Ö

Da der Wert von sin30^Ögleich 1/2 ist, können wir schreiben

Hypotenuse = Höhe / (1/2) = 2 × Höhe

Somit ist Hypotenuse = 2 × 8 = 16m

Somit beträgt die Länge der Hypotenuse 16 m.