Die Einschränkungen herkömmlicher binärer Suchbäume können frustrierend sein. Lernen Sie den B-Tree kennen, die multitalentierte Datenstruktur, die riesige Datenmengen problemlos verarbeiten kann. Wenn es darum geht, große Datenmengen zu speichern und zu durchsuchen, können herkömmliche binäre Suchbäume aufgrund ihrer schlechten Leistung und hohen Speichernutzung unpraktisch werden. B-Trees, auch bekannt als B-Tree oder Balanced Tree, sind eine Art selbstausgleichender Baum, der speziell zur Überwindung dieser Einschränkungen entwickelt wurde.
Im Gegensatz zu herkömmlichen binären Suchbäumen zeichnen sich B-Bäume durch die große Anzahl von Schlüsseln aus, die sie in einem einzelnen Knoten speichern können, weshalb sie auch als große Schlüsselbäume bezeichnet werden. Jeder Knoten in einem B-Baum kann mehrere Schlüssel enthalten, wodurch der Baum einen größeren Verzweigungsfaktor und damit eine geringere Höhe haben kann. Diese geringe Höhe führt zu weniger Festplatten-E/A, was zu schnelleren Such- und Einfügevorgängen führt. B-Trees eignen sich besonders gut für Speichersysteme mit langsamem, umfangreichem Datenzugriff wie Festplatten, Flash-Speicher und CD-ROMs.
B-Trees sorgt für das Gleichgewicht, indem sichergestellt wird, dass jeder Knoten über eine Mindestanzahl an Schlüsseln verfügt, sodass der Baum immer ausgeglichen ist. Dieses Gleichgewicht garantiert, dass die zeitliche Komplexität für Vorgänge wie Einfügen, Löschen und Suchen immer O(log n) beträgt, unabhängig von der ursprünglichen Form des Baums.
Zeitkomplexität des B-Baums:
| Herr Nr. | Algorithmus | Zeitkomplexität |
|---|---|---|
| 1. | Suchen | O(log n) |
| 2. | Einfügen | O(log n) |
| 3. | Löschen | O(log n) |
Notiz: n ist die Gesamtzahl der Elemente im B-Baum
Namen von Städten in den USA
Eigenschaften von B-Tree:
- Alle Blätter liegen auf gleicher Höhe.
- B-Baum wird durch den Begriff „Mindestgrad“ definiert. T ‘. Der Wert von ' T ' hängt von der Blockgröße der Festplatte ab.
- Jeder Knoten außer der Wurzel muss mindestens t-1 Schlüssel enthalten. Die Wurzel darf mindestens enthalten 1 Schlüssel.
- Alle Knoten (einschließlich Root) dürfen höchstens ( 2*t – 1 ) Schlüssel.
- Die Anzahl der Kinder eines Knotens entspricht der Anzahl der darin enthaltenen Schlüssel plus 1 .
- Alle Schlüssel eines Knotens werden in aufsteigender Reihenfolge sortiert. Das Kind zwischen zwei Schlüsseln k1 Und k2 enthält alle Schlüssel im Bereich von k1 Und k2 .
- Im Gegensatz zum binären Suchbaum wächst und schrumpft der B-Baum von der Wurzel aus. Binäre Suchbäume wachsen nach unten und schrumpfen auch nach unten.
- Wie bei anderen ausgeglichenen binären Suchbäumen beträgt die Zeitkomplexität zum Suchen, Einfügen und Löschen O(log n).
- Das Einfügen eines Knotens in den B-Baum erfolgt nur am Blattknoten.
Im Folgenden finden Sie ein Beispiel für einen B-Baum mit der Mindestordnung 5
Notiz: dass in praktischen B-Bäumen der Wert der Mindestordnung viel mehr als 5 beträgt.

Im obigen Diagramm können wir sehen, dass sich alle Blattknoten auf derselben Ebene befinden und alle Nicht-Blätter keinen leeren Unterbaum haben und Schlüssel haben, die um eins kleiner sind als die Anzahl ihrer untergeordneten Knoten.
Interessante Fakten über B-Bäume:
- Die minimale Höhe des B-Baums, die mit einer Anzahl von n Knoten existieren kann und m die maximale Anzahl von Kindern ist, die ein Knoten haben kann, beträgt:
- Die maximale Höhe des B-Baums, die mit einer Anzahl von n Knoten existieren kann und t die minimale Anzahl von Kindern ist, die ein Nicht-Wurzelknoten haben kann, beträgt:
Und
Durchquerung im B-Baum:
Die Durchquerung ähnelt auch der Inorder-Durchquerung des Binärbaums. Wir beginnen beim untergeordneten Element ganz links, geben das untergeordnete Element ganz links rekursiv aus und wiederholen dann den gleichen Vorgang für die verbleibenden untergeordneten Elemente und Schlüssel. Drucken Sie am Ende rekursiv das untergeordnete Element ganz rechts aus.
Java8-Funktionen
Suchvorgang im B-Baum:
Die Suche ähnelt der Suche im binären Suchbaum. Der zu suchende Schlüssel sei k.
- Beginnen Sie an der Wurzel und durchlaufen Sie rekursiv nach unten.
- Für jeden besuchten Nicht-Blattknoten
- Wenn der Knoten den Schlüssel hat, geben wir den Knoten einfach zurück.
- Andernfalls führen wir eine Wiederholung bis zum entsprechenden untergeordneten Knoten (dem untergeordneten Knoten, der unmittelbar vor dem ersten größeren Schlüssel liegt) des Knotens durch.
- Wenn wir einen Blattknoten erreichen und kein k im Blattknoten finden, geben wir NULL zurück.
Das Durchsuchen eines B-Baums ähnelt dem Durchsuchen eines Binärbaums. Der Algorithmus ist ähnlich und basiert auf Rekursion. Auf jeder Ebene wird die Suche so optimiert, dass, wenn der Schlüsselwert nicht im Bereich des übergeordneten Zweigs vorhanden ist, der Schlüssel in einem anderen Zweig vorhanden ist. Da diese Werte die Suche einschränken, werden sie auch als Grenzwerte oder Trennwerte bezeichnet. Wenn wir einen Blattknoten erreichen und den gewünschten Schlüssel nicht finden, wird NULL angezeigt.
Algorithmus zum Suchen eines Elements in einem B-Baum:-
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->key[i]) {> >i++;> >}> >if> (i n && k == x->key[i]) {> >return> x;> >}> >if> (x->Blatt) {> >return> nullptr;> >}> >return> BtreeSearch(x->child[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i]: i += 1 if i und k == x.key[i]: return x if x.leaf: return None return BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Beispiele:
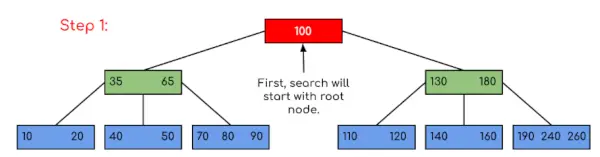
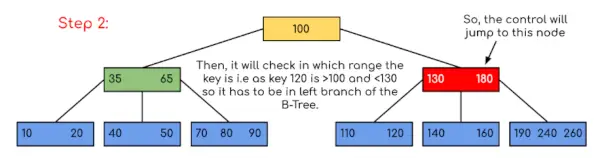
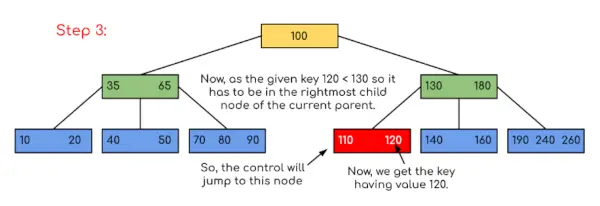
Eingang: Suchen Sie im angegebenen B-Baum nach 120.
Lösung:
arischer Khan
In diesem Beispiel können wir sehen, dass unsere Suche reduziert wurde, indem lediglich die Wahrscheinlichkeit eingeschränkt wurde, dass der Schlüssel, der den Wert enthält, vorhanden sein könnte. Wenn wir im obigen Beispiel nach 180 suchen müssen, stoppt die Steuerung ebenfalls bei Schritt 2, da das Programm feststellt, dass der Schlüssel 180 im aktuellen Knoten vorhanden ist. Und wenn 90 gesucht werden soll, dann gilt 90 <100, sodass automatisch zum linken Teilbaum gewechselt wird und der Kontrollfluss daher ähnlich verläuft wie im obigen Beispiel gezeigt.
Kapselung in Java
Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->search(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->Traverse(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->Traverse(); } // Funktion zum Suchen des Schlüssels k im Teilbaum, dessen Wurzel dieser Knoten ist BTreeNode* BTreeNode::search(int k) { // Den ersten Schlüssel finden, der größer oder gleich k ist int i = 0; while (i key[i]) i++; // Wenn der gefundene Schlüssel gleich k ist, gib diesen Knoten zurück. if (keys[i] == k) return this; // Wenn der Schlüssel hier nicht gefunden wird und dies ein Blattknoten ist, if (leaf == true) return NULL; // Gehe zum entsprechenden untergeordneten Element return C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>=> 0> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 und k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Teilen Sie das Kind auf def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] wenn nicht y.leaf: z.child = y.child[t: 2 * t] y. child = y.child[0: t - 1] # Den Baum drucken def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') für i in x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: für i in x.child: self.print_tree(i, l) # Suchschlüssel im Baum def search_key(self, k, x=None): wenn x nicht None ist: i = 0 while i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Notiz: Der obige Code enthält nicht das Treiberprogramm. Das komplette Programm werden wir in unserem nächsten Beitrag abdecken B-Baum-Einfügung .
Es gibt zwei Konventionen zum Definieren eines B-Baums: Die erste ist die Definition nach Mindestgrad und die zweite die Definition nach Reihenfolge. Wir haben die Mindestabschlusskonvention befolgt und werden diese auch in den kommenden Beiträgen auf B-Tree befolgen. Auch die im obigen Programm verwendeten Variablennamen bleiben gleich
Anwendungen von B-Bäumen:
- Es wird in großen Datenbanken verwendet, um auf die auf der Festplatte gespeicherten Daten zuzugreifen
- Die Suche nach Daten in einem Datensatz kann mit dem B-Tree in deutlich kürzerer Zeit durchgeführt werden
- Mit der Indizierungsfunktion kann eine mehrstufige Indizierung erreicht werden.
- Die meisten Server verwenden auch den B-Tree-Ansatz.
- B-Bäume werden in CAD-Systemen zum Organisieren und Durchsuchen geometrischer Daten verwendet.
- B-Bäume werden auch in anderen Bereichen wie der Verarbeitung natürlicher Sprache, Computernetzwerken und Kryptographie verwendet.
Vorteile von B-Bäumen:
- B-Bäume haben eine garantierte Zeitkomplexität von O(log n) für Grundoperationen wie Einfügen, Löschen und Suchen, wodurch sie für große Datenmengen und Echtzeitanwendungen geeignet sind.
- B-Bäume sind selbstausgleichend.
- Hohe Parallelität und hoher Durchsatz.
- Effiziente Speichernutzung.
Nachteile von B-Bäumen:
- B-Bäume basieren auf festplattenbasierten Datenstrukturen und können eine hohe Festplattenauslastung aufweisen.
- Nicht in allen Fällen das Beste.
- Langsam im Vergleich zu anderen Datenstrukturen.
Einfügen und Löschen:
B-Baum-Einfügung
B-Baum-Löschung