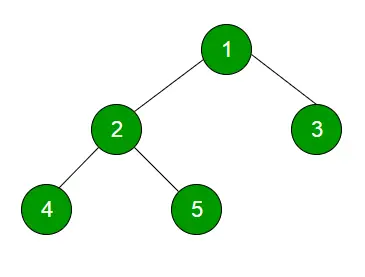
Level-Order-Traversal Die Technik ist definiert als eine Methode zum Durchlaufen eines Baums, sodass alle in derselben Ebene vorhandenen Knoten vollständig durchquert werden, bevor die nächste Ebene durchquert wird.

Beispiel:
Empfohlene Übungsstufe: Order Traversal Probieren Sie es aus!Eingang:
Ausgabe:
1
23
Vier fünf
Wie funktioniert Level Order Traversal?
Die Hauptidee der Ebenenreihenfolge-Durchquerung besteht darin, alle Knoten einer niedrigeren Ebene zu durchlaufen, bevor zu einem der Knoten einer höheren Ebene übergegangen wird. Dies kann auf eine der folgenden Arten erfolgen:
- die naive Variante (Ermitteln der Höhe des Baums, Durchlaufen jeder Ebene und Drucken der Knoten dieser Ebene)
- effiziente Nutzung einer Warteschlange.
Level Order Traversal (naiver Ansatz):
Finden Höhe von Baum. Führen Sie dann für jede Ebene eine rekursive Funktion aus, indem Sie die aktuelle Höhe beibehalten. Wenn die Ebene eines Knotens übereinstimmt, drucken Sie diesen Knoten aus.
Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:
C++ // Recursive CPP program for level // order traversal of Binary Tree #include using namespace std; // A binary tree node has data, // pointer to left child // and a pointer to right child class node { public: int data; node *left, *right; }; // Function prototypes void printCurrentLevel(node* root, int level); int height(node* node); node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(node* root, int level) { if (root == NULL) return; if (level == 1) cout << root->Daten<< ' '; else if (level>1) { printCurrentLevel(root->left, level - 1); printCurrentLevel(root->right, level - 1); } } // Berechne die „Höhe“ eines Baums – die Anzahl der // Knoten entlang des längsten Pfads vom Wurzelknoten // bis zum am weitesten entfernten Blattknoten. int height(node* node) { if (node == NULL) return 0; else { // Berechne die Höhe jedes Teilbaums int lheight = height(node->left); int rheight = height(node->right); // Den größeren verwenden if (lheight> rheight) { return (lheight + 1); } else { return (rheight + 1); } } } // Hilfsfunktion, die // einen neuen Knoten mit den angegebenen Daten und // NULL-Links- und -Rechtszeigern zuweist. node* newNode(int data) { node* Node = new node(); Knoten->Daten = Daten; Node->left = NULL; Knoten->rechts = NULL; return (Knoten); } // Treibercode int main() { node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; } // This code is contributed by rathbhupendra> C // Recursive C program for level // order traversal of Binary Tree #include #include // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node *left, *right; }; // Function prototypes void printCurrentLevel(struct node* root, int level); int height(struct node* node); struct node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(struct node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(struct node* root, int level) { if (root == NULL) return; if (level == 1) printf('%d ', root->Daten); else if (level> 1) { printCurrentLevel(root->left, level - 1); printCurrentLevel(root->right, level - 1); } } // Berechne die 'Höhe' eines Baums – die Anzahl der // Knoten entlang des längsten Pfads vom Wurzelknoten // bis zum am weitesten entfernten Blattknoten int height(struct node* node) { if (node == NULL) return 0; else { // Berechne die Höhe jedes Teilbaums int lheight = height(node->left); int rheight = height(node->right); // Den größeren verwenden if (lheight> rheight) return (lheight + 1); sonst return (right + 1); } } // Hilfsfunktion, die einen neuen Knoten mit den // angegebenen Daten und NULL-Links- und -Rechtszeigern zuweist. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); Knoten->Daten = Daten; node->left = NULL; node->right = NULL; return (Knoten); } // Treiberprogramm zum Testen der oben genannten Funktionen int main() { struct node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); printf('Level Order Traversal des Binärbaums ist
'); printLevelOrder(root); 0 zurückgeben; }> Java // Recursive Java program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { int data; Node left, right; public Node(int item) { data = item; left = right = null; } } class BinaryTree { // Root of the Binary Tree Node root; public BinaryTree() { root = null; } // Function to print level order traversal of tree void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number of // nodes along the longest path from the root node // down to the farthest leaf node. int height(Node root) { if (root == null) return 0; else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>rheight) return (lheight + 1); sonst return (right + 1); } } // Knoten auf der aktuellen Ebene drucken void printCurrentLevel(Node root, int level) { if (root == null) return; if (level == 1) System.out.print(root.data + ' '); else if (level> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, level - 1); } } // Treiberprogramm zum Testen der oben genannten Funktionen public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = neuer Knoten(1); tree.root.left = neuer Knoten(2); tree.root.right = neuer Knoten(3); tree.root.left.left = neuer Knoten(4); tree.root.left.right = neuer Knoten(5); System.out.println('Level order traversal of' + 'binary tree is '); tree.printLevelOrder(); } }> Python # Recursive Python program for level # order traversal of Binary Tree # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Function to print level order traversal of tree def printLevelOrder(root): h = height(root) for i in range(1, h+1): printCurrentLevel(root, i) # Print nodes at a current level def printCurrentLevel(root, level): if root is None: return if level == 1: print(root.data, end=' ') elif level>1: printCurrentLevel(root.left, level-1) printCurrentLevel(root.right, level-1) # Berechnen Sie die Höhe eines Baums – die Anzahl der Knoten # entlang des längsten Pfads vom Wurzelknoten bis zum # am weitesten entfernten Blatt node def height(node): wenn node None ist: 0 zurückgeben sonst: # Berechnen Sie die Höhe jedes Teilbaums lheight = height(node.left) rheight = height(node.right) # Verwenden Sie den größeren, wenn lheight> rheight: return lheight+1 else: return rheight+1 # Treiberprogramm zum Testen der obigen Funktion, wenn __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root. left.left = Node(4) root.left.right = Node(5) print('Level Order Traversal of Binary Tree is -') printLevelOrder(root) # Dieser Code wurde von Nikhil Kumar Singh(nickzuck_007)> beigesteuert C# // Recursive c# program for level // order traversal of Binary Tree using System; // Class containing left and right // child of current node and key value public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { // Root of the Binary Tree public Node root; public void BinaryTree() { root = null; } // Function to print level order // traversal of tree public virtual void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) { printCurrentLevel(root, i); } } // Compute the 'height' of a tree -- // the number of nodes along the longest // path from the root node down to the // farthest leaf node. public virtual int height(Node root) { if (root == null) { return 0; } else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>rheight) { return (lheight + 1); } else { return (rheight + 1); } } } // Knoten auf der aktuellen Ebene drucken public virtual void printCurrentLevel(Node root, int level) { if (root == null) { return; } if (level == 1) { Console.Write(root.data + ' '); } else if (level> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, level - 1); } } // Treibercode public static void Main(string[] args) { GFG tree = new GFG(); tree.root = neuer Knoten(1); tree.root.left = neuer Knoten(2); tree.root.right = neuer Knoten(3); tree.root.left.left = neuer Knoten(4); tree.root.left.right = neuer Knoten(5); Console.WriteLine('Level Order Traversal ' + 'of Binary Tree is '); tree.printLevelOrder(); } } // Dieser Code wurde von Shrikant13>'> beigesteuertJavascriptrheight) return (lheight + 1); sonst return (right + 1); } } // Knoten auf der aktuellen Ebene drucken function printCurrentLevel(root , level) { if (root == null) return; if (level == 1) console.log(root.data + ' '); else if (level> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, level - 1); } } // Treiberprogramm zum Testen der oben genannten Funktionen root = new Node(1); root.left = neuer Knoten(2); root.right = neuer Knoten(3); root.left.left = neuer Knoten(4); root.left.right = neuer Knoten(5); console.log('Durchquerung der Ebenenreihenfolge des Binärbaums ist '); printLevelOrder(); // Dieser Code wurde von umadevi9616>'> beigesteuert
Ausgabe Level Order traversal of binary tree is 1 2 3 4 5>
Zeitkomplexität: O(N), wobei N die Anzahl der Knoten im verzerrten Baum ist.
Hilfsraum: O(1) Wenn der Rekursionsstapel berücksichtigt wird, ist der verwendete Speicherplatz O(N).
Datumszeichenfolge Java
Level Order Traversal mit Warteschlange
Wir müssen die Knoten auf einer niedrigeren Ebene vor jedem Knoten auf einer höheren Ebene besuchen. Diese Idee ähnelt der einer Warteschlange. Schieben Sie die Knoten einer niedrigeren Ebene in die Warteschlange. Wenn ein Knoten besucht wird, entfernen Sie diesen Knoten aus der Warteschlange und verschieben Sie das untergeordnete Element dieses Knotens in die Warteschlange.
Dadurch wird sichergestellt, dass die Knoten einer niedrigeren Ebene vor allen Knoten einer höheren Ebene besucht werden.
Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:
C++ // C++ program to print level order traversal #include using namespace std; // A Binary Tree Node struct Node { int data; struct Node *left, *right; }; // Iterative method to find height of Binary Tree void printLevelOrder(Node* root) { // Base Case if (root == NULL) return; // Create an empty queue for level order traversal queueQ; // Root in die Warteschlange stellen und Höhe initialisieren q.push(root); while (q.empty() == false) { // Vorderseite der Warteschlange drucken und aus der Warteschlange entfernen Node* node = q.front(); cout<< node->Daten<< ' '; q.pop(); // Enqueue left child if (node->left != NULL) q.push(node->left); // Rechtes Kind in die Warteschlange stellen if (node->right != NULL) q.push(node->right); } } // Hilfsfunktion zum Erstellen eines neuen Baumknotens Node* newNode(int data) { Node* temp = new Node; temp->data = data; temp->left = temp->right = NULL; Rücklauftemperatur; } // Treiberprogramm zum Testen der oben genannten Funktionen int main() { // Lassen Sie uns den im obigen Diagramm gezeigten Binärbaum erstellen Node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; }> C // Iterative Queue based C program // to do level order traversal // of Binary Tree #include #include #define MAX_Q_SIZE 500 // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node* left; struct node* right; }; // Function prototypes struct node** createQueue(int*, int*); void enQueue(struct node**, int*, struct node*); struct node* deQueue(struct node**, int*); // Given a binary tree, print its nodes in level order // using array for implementing queue void printLevelOrder(struct node* root) { int rear, front; struct node** queue = createQueue(&front, &rear); struct node* temp_node = root; while (temp_node) { printf('%d ', temp_node->Daten); // Linkes Kind in die Warteschlange stellen if (temp_node->left) enQueue(queue, &rear, temp_node->left); // Rechtes Kind in die Warteschlange stellen if (temp_node->right) enQueue(queue, &rear, temp_node->right); // Knoten aus der Warteschlange entfernen und zu temp_node machen temp_node = deQueue(queue, &front); } } // Dienstprogrammfunktionen struct node** createQueue(int* front, int* Rear) { struct node** queue = (struct node**)malloc( sizeof(struct node*) * MAX_Q_SIZE); *vorne = *hinten = 0; Rückgabewarteschlange; } void enQueue(struct node** queue, int* Rear, struct node* new_node) { queue[*rear] = new_node; (*hinten)++; } struct node* deQueue(struct node** queue, int* front) { (*front)++; return queue[*front - 1]; } // Hilfsfunktion, die einen neuen Knoten mit den // angegebenen Daten und NULL-Links- und -Rechtszeigern zuweist. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); Knoten->Daten = Daten; node->left = NULL; node->right = NULL; return (Knoten); } // Treiberprogramm zum Testen der oben genannten Funktionen int main() { struct node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); printf('Level Order Traversal des Binärbaums ist
'); printLevelOrder(root); 0 zurückgeben; }> Java // Iterative Queue based Java program // to do level order traversal // of Binary Tree import java.util.LinkedList; import java.util.Queue; // Class to represent Tree node class Node { int data; Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order // using array for implementing queue void printLevelOrder() { Queuequeue = neue LinkedList(); queue.add(root); while (!queue.isEmpty()) { // poll() entfernt den aktuellen Kopf. Knoten tempNode = queue.poll(); System.out.print(tempNode.data + ' '); // Linkes Kind in die Warteschlange stellen if (tempNode.left != null) { queue.add(tempNode.left); } // Rechtes Kind in die Warteschlange stellen if (tempNode.right != null) { queue.add(tempNode.right); } } } public static void main(String args[]) { // Einen Binärbaum erstellen und // die Knoten eingeben BinaryTree tree_level = new BinaryTree(); tree_level.root = neuer Knoten(1); tree_level.root.left = neuer Knoten(2); tree_level.root.right = neuer Knoten(3); tree_level.root.left.left = neuer Knoten(4); tree_level.root.left.right = neuer Knoten(5); System.out.println('Durchquerung der Ebenenreihenfolge des Binärbaums ist - '); tree_level.printLevelOrder(); } }> Python # Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Vorderseite der Warteschlange drucken und # aus der Warteschlange entfernen print(queue[0].data, end=' ') node = queue.pop(0) # Linkes Kind in die Warteschlange stellen, wenn node.left nicht None ist: queue.append(node.left) # Rechtes Kind in die Warteschlange stellen, wenn node.right nicht None ist: queue.append(node.right) # Treiberprogramm zum Testen der obigen Funktion, wenn __name__ == '__main__': root = Node(1 ) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Level Order Traversal des Binärbaums ist - ') printLevelOrder(root) # Dieser Code wurde von Nikhil Kumar Singh(nickzuck_007) beigesteuert> C# // Iterative Queue based C# program // to do level order traversal // of Binary Tree using System; using System.Collections.Generic; // Class to represent Tree node public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal public class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order using // array for implementing queue void printLevelOrder() { Queuequeue = neue Warteschlange(); queue.Enqueue(root); while (queue.Count != 0) { Node tempNode = queue.Dequeue(); Console.Write(tempNode.data + ' '); // Linkes Kind in die Warteschlange stellen if (tempNode.left != null) { queue.Enqueue(tempNode.left); } // Rechtes Kind in die Warteschlange stellen if (tempNode.right != null) { queue.Enqueue(tempNode.right); } } } // Treibercode public static void Main() { // Binärbaum erstellen und // die Knoten eingeben BinaryTree tree_level = new BinaryTree(); tree_level.root = neuer Knoten(1); tree_level.root.left = neuer Knoten(2); tree_level.root.right = neuer Knoten(3); tree_level.root.left.left = neuer Knoten(4); tree_level.root.left.right = neuer Knoten(5); Console.WriteLine('Level Order Traversal ' + 'of Binary Tree is - '); tree_level.printLevelOrder(); } } // Dieser Code wurde von PrinciRaj1992 beigesteuert> Javascript class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Class to represent a deque (double-ended queue) class Deque { constructor() { this.queue = []; } // Method to add an element to the end of the queue enqueue(item) { this.queue.push(item); } // Method to remove and return the first element of the queue dequeue() { return this.queue.shift(); } // Method to check if the queue is empty isEmpty() { return this.queue.length === 0; } } // Function to perform level order traversal of a binary tree function printLevelOrder(root) { // Create a deque to store nodes for traversal const queue = new Deque(); // Add the root node to the queue queue.enqueue(root); // Continue traversal until the queue is empty while (!queue.isEmpty()) { // Remove and get the first node from the queue const tempNode = queue.dequeue(); // Print the data of the current node console.log(tempNode.data + ' '); // Enqueue the left child if it exists if (tempNode.left !== null) { queue.enqueue(tempNode.left); } // Enqueue the right child if it exists if (tempNode.right !== null) { queue.enqueue(tempNode.right); } } } // Create a binary tree and enter the nodes const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); // Print the level order traversal of the binary tree console.log('Level order traversal of binary tree is - '); printLevelOrder(root);> Ausgabe
Hilfsraum: O(N) wobei N die Anzahl der Knoten im Binärbaum ist.