In der realen Welt maschinelles Lernen In Anwendungen gibt es häufig viele relevante Merkmale, von denen jedoch möglicherweise nur eine Teilmenge beobachtbar ist. Beim Umgang mit Variablen, die manchmal beobachtbar sind und manchmal nicht, ist es tatsächlich möglich, die Fälle zu nutzen, in denen diese Variable sichtbar oder beobachtet ist, um zu lernen und Vorhersagen für die Fälle zu treffen, in denen sie nicht beobachtbar ist. Dieser Ansatz wird oft als Umgang mit fehlenden Daten bezeichnet. Mithilfe der verfügbaren Instanzen, in denen die Variable beobachtbar ist, können Algorithmen für maschinelles Lernen Muster und Beziehungen aus den beobachteten Daten lernen. Diese gelernten Muster können dann verwendet werden, um die Werte der Variablen in Fällen vorherzusagen, in denen sie fehlt oder nicht beobachtbar ist.
Der Erwartungsmaximierungsalgorithmus kann zur Handhabung von Situationen verwendet werden, in denen Variablen teilweise beobachtbar sind. Wenn bestimmte Variablen beobachtbar sind, können wir diese Instanzen verwenden, um ihre Werte zu lernen und abzuschätzen. Dann können wir die Werte dieser Variablen in Fällen vorhersagen, in denen sie nicht beobachtbar sind.
Der EM-Algorithmus wurde 1977 in einer wegweisenden Arbeit von Arthur Dempster, Nan Laird und Donald Rubin vorgeschlagen und benannt. Ihre Arbeit formalisierte den Algorithmus und demonstrierte seine Nützlichkeit bei der statistischen Modellierung und Schätzung.
Der EM-Algorithmus ist auf latente Variablen anwendbar, bei denen es sich um Variablen handelt, die nicht direkt beobachtbar sind, sondern aus den Werten anderer beobachteter Variablen abgeleitet werden. Durch Nutzung der bekannten allgemeinen Form der Wahrscheinlichkeitsverteilung, die diese latenten Variablen bestimmt, kann der EM-Algorithmus ihre Werte vorhersagen.
Der EM-Algorithmus dient als Grundlage für viele unbeaufsichtigte Clustering-Algorithmen im Bereich des maschinellen Lernens. Es bietet einen Rahmen zum Ermitteln der lokalen Maximum-Likelihood-Parameter eines statistischen Modells und zum Ableiten latenter Variablen in Fällen, in denen Daten fehlen oder unvollständig sind.
Expectation-Maximization (EM)-Algorithmus
Der Expectation-Maximization (EM)-Algorithmus ist eine iterative Optimierungsmethode, die verschiedene unbeaufsichtigte Methoden kombiniert maschinelles Lernen Algorithmen zum Finden von Maximum-Likelihood- oder Maximum-Posteriori-Schätzungen von Parametern in statistischen Modellen, die unbeobachtete latente Variablen beinhalten. Der EM-Algorithmus wird häufig für latente Variablenmodelle verwendet und kann fehlende Daten verarbeiten. Es besteht aus einem Schätzschritt (E-Schritt) und einem Maximierungsschritt (M-Schritt) und bildet einen iterativen Prozess zur Verbesserung der Modellanpassung.
- Im E-Schritt berechnet der Algorithmus die latenten Variablen, d. h. die Erwartung der Log-Likelihood, unter Verwendung der aktuellen Parameterschätzungen.
- Im M-Schritt bestimmt der Algorithmus die Parameter, die die im E-Schritt erhaltene erwartete Log-Likelihood maximieren, und entsprechende Modellparameter werden basierend auf den geschätzten latenten Variablen aktualisiert.

Erwartungsmaximierung im EM-Algorithmus
Durch die iterative Wiederholung dieser Schritte versucht der EM-Algorithmus, die Wahrscheinlichkeit der beobachteten Daten zu maximieren. Es wird häufig für unbeaufsichtigte Lernaufgaben wie Clustering verwendet, bei dem latente Variablen abgeleitet werden, und findet in verschiedenen Bereichen Anwendung, darunter maschinelles Lernen, Computer Vision und Verarbeitung natürlicher Sprache.
Schlüsselbegriffe im Expectation-Maximization (EM)-Algorithmus
Einige der am häufigsten verwendeten Schlüsselbegriffe im Expectation-Maximization (EM)-Algorithmus sind wie folgt:
- Latente Variablen: Latente Variablen sind unbeobachtete Variablen in statistischen Modellen, die nur indirekt durch ihre Auswirkungen auf beobachtbare Variablen abgeleitet werden können. Sie können nicht direkt gemessen werden, können aber anhand ihrer Auswirkung auf die beobachtbaren Variablen erkannt werden. Wahrscheinlichkeit: Dies ist die Wahrscheinlichkeit, dass die gegebenen Daten angesichts der Parameter des Modells beobachtet werden. Das Ziel des EM-Algorithmus besteht darin, die Parameter zu finden, die die Wahrscheinlichkeit maximieren. Log-Likelihood: Dabei handelt es sich um den Logarithmus der Likelihood-Funktion, der die Güte der Übereinstimmung zwischen den beobachteten Daten und dem Modell misst. Der EM-Algorithmus versucht, die Log-Likelihood zu maximieren. Maximum-Likelihood-Schätzung (MLE): MLE ist eine Methode zur Schätzung der Parameter eines statistischen Modells, indem die Parameterwerte ermittelt werden, die die Wahrscheinlichkeitsfunktion maximieren, die misst, wie gut das Modell die beobachteten Daten erklärt. Posterior-Wahrscheinlichkeit: Im Kontext der Bayes'schen Inferenz kann der EM-Algorithmus erweitert werden, um die maximalen a-posteriori-Schätzungen (MAP) zu schätzen, wobei die Posterior-Wahrscheinlichkeit der Parameter auf der Grundlage der A-priori-Verteilung und der Likelihood-Funktion berechnet wird. Erwartungsschritt (E): Der E-Schritt des EM-Algorithmus berechnet den erwarteten Wert oder die A-posteriori-Wahrscheinlichkeit der latenten Variablen anhand der beobachteten Daten und aktuellen Parameterschätzungen. Dabei werden die Wahrscheinlichkeiten jeder latenten Variablen für jeden Datenpunkt berechnet. Maximierungsschritt (M): Der M-Schritt des EM-Algorithmus aktualisiert die Parameterschätzungen durch Maximieren der erwarteten Log-Likelihood, die aus dem E-Schritt erhalten wird. Dabei geht es darum, die Parameterwerte zu finden, die die Likelihood-Funktion optimieren, typischerweise durch numerische Optimierungsmethoden. Konvergenz: Konvergenz bezieht sich auf den Zustand, in dem der EM-Algorithmus eine stabile Lösung erreicht hat. Dies wird in der Regel dadurch ermittelt, dass überprüft wird, ob die Änderung der Log-Likelihood oder der Parameterschätzungen unter einen vordefinierten Schwellenwert fällt.
So funktioniert der Expectation-Maximization (EM)-Algorithmus:
Der Kern des Expectation-Maximization-Algorithmus besteht darin, die verfügbaren beobachteten Daten des Datensatzes zu verwenden, um die fehlenden Daten zu schätzen und diese Daten dann zum Aktualisieren der Werte der Parameter zu verwenden. Lassen Sie uns den EM-Algorithmus im Detail verstehen.

Flussdiagramm des EM-Algorithmus
- Initialisierung:
- Zunächst wird eine Reihe von Anfangswerten der Parameter betrachtet. Dem System wird ein Satz unvollständiger beobachteter Daten übergeben, wobei davon ausgegangen wird, dass die beobachteten Daten von einem bestimmten Modell stammen.
- Berechnen Sie die A-posteriori-Wahrscheinlichkeit oder Verantwortlichkeit jeder latenten Variablen anhand der beobachteten Daten und aktuellen Parameterschätzungen.
- Schätzen Sie die fehlenden oder unvollständigen Datenwerte anhand der aktuellen Parameterschätzungen.
- Berechnen Sie die Log-Likelihood der beobachteten Daten basierend auf den aktuellen Parameterschätzungen und den geschätzten fehlenden Daten.
- Aktualisieren Sie die Parameter des Modells, indem Sie die erwartete vollständige Datenprotokollwahrscheinlichkeit maximieren, die aus dem E-Schritt erhalten wird.
- Dies beinhaltet typischerweise die Lösung von Optimierungsproblemen, um die Parameterwerte zu finden, die die Log-Likelihood maximieren.
- Die verwendete spezifische Optimierungstechnik hängt von der Art des Problems und dem verwendeten Modell ab.
- Überprüfen Sie die Konvergenz, indem Sie die Änderung der Log-Likelihood oder der Parameterwerte zwischen Iterationen vergleichen.
- Wenn die Änderung unter einem vordefinierten Schwellenwert liegt, halten Sie an und gehen Sie davon aus, dass der Algorithmus konvergiert ist.
- Andernfalls kehren Sie zum E-Schritt zurück und wiederholen Sie den Vorgang, bis die Konvergenz erreicht ist.
Schrittweise Implementierung des Erwartungsmaximierungsalgorithmus
Importieren Sie die erforderlichen Bibliotheken
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
>
Generieren Sie einen Datensatz mit zwei Gaußschen Komponenten
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
tun, während Java
Ausgabe :

Dichtediagramm
Parameter initialisieren
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Führen Sie den EM-Algorithmus durch
- Iteriert für die angegebene Anzahl von Epochen (in diesem Fall 20).
- In jeder Epoche berechnet der E-Schritt die Verantwortlichkeiten (Gammawerte), indem er die Gaußschen Wahrscheinlichkeitsdichten für jede Komponente auswertet und sie mit den entsprechenden Anteilen gewichtet.
- Der M-Schritt aktualisiert die Parameter, indem er den gewichteten Mittelwert und die Standardabweichung für jede Komponente berechnet
Python3
wie viele Wochen pro Monat
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Ausgabe :

Epoche vs. Log-Wahrscheinlichkeit
Zeichnen Sie die endgültige geschätzte Dichte grafisch auf
Python3
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Ausgabe :
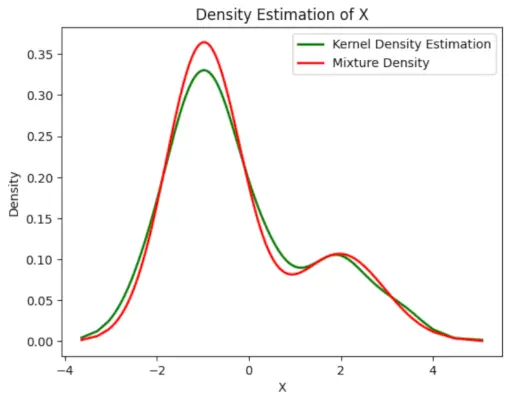
Geschätzte Dichte
Anwendungen der EM-Algorithmus
- Es kann verwendet werden, um die fehlenden Daten in einer Probe zu ergänzen.
- Es kann als Grundlage für das unbeaufsichtigte Lernen von Clustern verwendet werden.
- Es kann zur Schätzung der Parameter des Hidden-Markov-Modells (HMM) verwendet werden.
- Es kann zur Ermittlung der Werte latenter Variablen verwendet werden.
Vorteile des EM-Algorithmus
- Es ist immer garantiert, dass die Wahrscheinlichkeit mit jeder Iteration zunimmt.
- Der E-Schritt und der M-Schritt sind bei vielen Problemen in der Umsetzung oft recht einfach.
- Lösungen für die M-Schritte liegen häufig in geschlossener Form vor.
Nachteile des EM-Algorithmus
- Es hat eine langsame Konvergenz.
- Es erfolgt nur eine Konvergenz zu den lokalen Optima.
- Es erfordert sowohl die Vorwärts- als auch die Rückwärtswahrscheinlichkeit (die numerische Optimierung erfordert nur die Vorwärtswahrscheinlichkeit).
