Voraussetzung: Lineare Regression
Lineare Regression ist ein maschineller Lernalgorithmus, der auf überwachtem Lernen basiert. Es führt eine Regressionsaufgabe aus. Die Regression modelliert einen Zielvorhersagewert basierend auf unabhängigen Variablen. Es wird hauptsächlich verwendet, um die Beziehung zwischen Variablen und Prognosen herauszufinden. Verschiedene Regressionsmodelle unterscheiden sich basierend auf – der Art der Beziehung zwischen den abhängigen und unabhängigen Variablen, die sie berücksichtigen, und der Anzahl der verwendeten unabhängigen Variablen. In diesem Artikel wird gezeigt, wie Sie die verschiedenen Python-Bibliotheken verwenden, um eine lineare Regression für einen bestimmten Datensatz zu implementieren. Wir werden ein binäres lineares Modell demonstrieren, da dieses einfacher zu visualisieren ist. In dieser Demonstration verwendet das Modell Gradient Descent zum Lernen. Hier können Sie mehr darüber erfahren.
Schritt 1: Importieren aller erforderlichen Bibliotheken
Python3
import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn>import> preprocessing, svm> from> sklearn.model_selection>import> train_test_split> from> sklearn.linear_model>import> LinearRegression> |
>
>
Schritt 2: Lesen des Datensatzes:
Python3
df>=> pd.read_csv(>'bottle.csv'>)> df_binary>=> df[[>'Salnty'>,>'T_degC'>]]> > # Taking only the selected two attributes from the dataset> df_binary.columns>=> [>'Sal'>,>'Temp'>]> #display the first 5 rows> df_binary.head()> |
Schlaf für Javascript
>
>
Ausgabe:
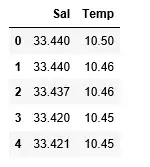
Schritt 3: Erkundung der Datenstreuung
Python3
#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary, order>=> 2>, ci>=> None>)> plt.show()> |
>
c Zufallszahl
>
Ausgabe:

Schritt 4: Datenreinigung
Python3
# Eliminating NaN or missing input numbers> df_binary.fillna(method>=>'ffill'>, inplace>=> True>)> |
>
>
Schritt 5: Training unseres Modells
Python3
X>=> np.array(df_binary[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary[>'Temp'>]).reshape(>->1>,>1>)> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace>=> True>)> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > # Splitting the data into training and testing data> regr>=> LinearRegression()> > regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
Java-Hashset
>
>
Ausgabe:

Schritt 6: Entdecken Sie unsere Ergebnisse
Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> # Data scatter of predicted values> |
>
>
Ausgabe:

Der niedrige Genauigkeitswert unseres Modells lässt darauf schließen, dass unser regressives Modell nicht sehr gut zu den vorhandenen Daten passt. Dies deutet darauf hin, dass unsere Daten nicht für eine lineare Regression geeignet sind. Aber manchmal akzeptiert ein Datensatz möglicherweise einen linearen Regressor, wenn wir nur einen Teil davon betrachten. Lassen Sie uns diese Möglichkeit prüfen.
Schritt 7: Arbeiten mit einem kleineren Datensatz
Python3
df_binary500>=> df_binary[:][:>500>]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary500,> >order>=> 2>, ci>=> None>)> |
>
>
Ausgabe:
Datenstrukturen in Java

Wir können bereits erkennen, dass die ersten 500 Zeilen einem linearen Modell folgen. Fahren Sie mit den gleichen Schritten wie zuvor fort.
Python3
df_binary500.fillna(method>=>'fill'>, inplace>=> True>)> > X>=> np.array(df_binary500[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary500[>'Temp'>]).reshape(>->1>,>1>)> > df_binary500.dropna(inplace>=> True>)> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > regr>=> LinearRegression()> regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
Ausgabe:

Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> |
Prime kein Code in Java
>
>
Ausgabe:

Schritt 8: Bewertungsmetriken für die Regression
Abschließend überprüfen wir die Leistung des linearen Regressionsmodells mithilfe von Bewertungsmetriken. Für Regressionsalgorithmen verwenden wir häufig die Metriken „mean_absolute_error“ und „mean_squared_error“, um die Modellleistung zu überprüfen.
Python3
from> sklearn.metrics>import> mean_absolute_error,mean_squared_error> > mae>=> mean_absolute_error(y_true>=>y_test,y_pred>=>y_pred)> #squared True returns MSE value, False returns RMSE value.> mse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred)>#default=True> rmse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred,squared>=>False>)> > print>(>'MAE:'>,mae)> print>(>'MSE:'>,mse)> print>(>'RMSE:'>,rmse)> |
>
>
Ausgabe:
MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078>
