Topologische Sortierung für Gerichteter azyklischer Graph (DAG) ist eine lineare Anordnung von Scheitelpunkten, sodass für jede gerichtete Kante u-v ein Scheitelpunkt gilt In kommt davor In in der Bestellung.
Notiz: Eine topologische Sortierung für einen Graphen ist nicht möglich, wenn der Graph kein ist TAG .
Beispiel:
Empfohlene PraxisDFS-basierte Lösung zum Finden einer topologischen Sortierung wurde bereits besprochen.Eingang: Grafik:
Beispiel
Ausgabe: 5 4 2 3 1 0
Erläuterung: Der erste Scheitelpunkt bei der topologischen Sortierung ist immer ein Scheitelpunkt mit einem In-Grad von 0 (ein Scheitelpunkt ohne eingehende Kanten). Eine topologische Sortierung des folgenden Diagramms ist 5 4 2 3 1 0. Es kann mehr als eine topologische Sortierung für ein Diagramm geben. Eine andere topologische Sortierung des folgenden Diagramms ist 4 5 2 3 1 0.
Die topologische Reihenfolge ist möglicherweise nicht eindeutig:
Topologische Sortierung ist ein Abhängigkeitsproblem, bei dem die Erledigung einer Aufgabe von der Erledigung mehrerer anderer Aufgaben abhängt, deren Reihenfolge variieren kann. Lassen Sie uns dieses Konzept anhand eines Beispiels verstehen:
Angenommen, unsere Aufgabe besteht darin, unsere Schule zu erreichen, und um dorthin zu gelangen, müssen wir uns zuerst anziehen. Die Abhängigkeiten beim Tragen von Kleidung sind im folgenden Abhängigkeitsdiagramm dargestellt. Beispielsweise können Sie keine Schuhe anziehen, bevor Sie Socken tragen.
Anhand des Bildes oben hätten Sie bereits erkennen können, dass es mehrere Möglichkeiten gibt, sich anzuziehen. Das Bild unten zeigt einige dieser Möglichkeiten.
Können Sie auflisten? alle möglichen topologischen Ordnungen wie man sich für das obige Abhängigkeitsdiagramm anzieht?
Algorithmus zur topologischen Sortierung mit DFS:
Hier ist ein Schritt-für-Schritt-Algorithmus für die topologische Sortierung mithilfe der Tiefensuche (Depth First Search, DFS):
- Erstellen Sie ein Diagramm mit N Eckpunkte und M -gerichtete Kanten.
- Initialisieren Sie einen Stapel und ein besuchtes Array mit einer bestimmten Größe N .
- Gehen Sie für jeden nicht besuchten Scheitelpunkt im Diagramm wie folgt vor:
- Rufen Sie die DFS-Funktion mit dem Scheitelpunkt als Parameter auf.
- Markieren Sie in der DFS-Funktion den Scheitelpunkt als besucht und rufen Sie die DFS-Funktion rekursiv für alle nicht besuchten Nachbarn des Scheitelpunkts auf.
- Sobald alle Nachbarn besucht wurden, schieben Sie den Scheitelpunkt auf den Stapel.
- Nachdem alle Knoten besucht wurden, entfernen Sie Elemente aus dem Stapel und hängen Sie sie an die Ausgabeliste an, bis der Stapel leer ist.
- Die resultierende Liste ist die topologisch sortierte Reihenfolge des Diagramms.
Abbildung Topologischer Sortieralgorithmus:
Das folgende Bild veranschaulicht den oben genannten Ansatz:

Gesamtablauf der topologischen Sortierung
Schritt 1:
- Wir starten DFS von Knoten 0 aus, da es keine eingehenden Knoten hat
- Wir schieben Knoten 0 in den Stapel und gehen zum nächsten Knoten mit der minimalen Anzahl benachbarter Knoten, d. h. Knoten 1.
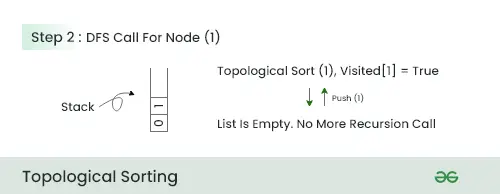
Schritt 2:
- Da zu diesem Knoten kein Nachbarknoten vorhanden ist, schieben Sie in diesem Schritt den Knoten 1 in den Stapel und gehen Sie zum nächsten Knoten.
Azure-AbonnementSchritt 3:
- In diesem Schritt wählen wir Knoten 2, da er nach 0 und 1 die minimale Anzahl benachbarter Knoten aufweist.
- Wir rufen DFS für Knoten 2 auf und pushen alle Knoten, die von Knoten 2 durchlaufen werden, in umgekehrter Reihenfolge.
- Drücken Sie also 3 und dann 2.
Schritt 4:
- Wir rufen nun DFS für Knoten 4 auf
- Da 0 und 1 bereits im Stapel vorhanden sind, schieben wir einfach Knoten 4 in den Stapel und kehren zurück.
Schritt 5:
- Da sich in diesem Schritt alle benachbarten Knoten von 5 bereits im Stapel befinden, schieben wir Knoten 5 in den Stapel und kehren zurück.
Schritt 6: Dies ist der letzte Schritt der topologischen Sortierung, bei dem wir alle Elemente aus dem Stapel nehmen und in dieser Reihenfolge drucken.
Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, Vektor & besucht, Stapel & Stack) { // Markiere den aktuellen Knoten als besucht besuchte[v] = true; // Wiederholung für alle benachbarten Scheitelpunkte for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, besuchte, Stack); } // Aktuellen Scheitelpunkt in den Stapel verschieben, der das Ergebnis speichert Stack.push(v); } // Funktion zur Durchführung einer topologischen Sortierung void topologicalSort(vector>& adj, int V) { stack Stapel; // Stapel zum Speichern des Ergebnisvektors besuchte(V, falsch); // Rufen Sie die rekursive Hilfsfunktion zum Speichern auf. // Topologische Sortierung ausgehend von allen Eckpunkten nacheinander // einzeln für (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> Kanten = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Diagramm dargestellt als Adjazenzlistenvektor> adj(V); for (auto i : Kanten) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, boolean[] besuchte, Stack stack) { // Markiere den aktuellen Knoten als besucht besuchte[v] = true; // Wiederholen für alle benachbarten Scheitelpunkte for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, besuchte, stack); } // Aktuellen Scheitelpunkt in den Stapel verschieben, der das // Ergebnis speichert stack.push(v); } // Funktion zur Durchführung einer topologischen Sortierung static void topologicalSort(List> adj, int V) { // Stack zum Speichern des Ergebnisses Stack stack = new Stack(); boolean[] besuchte = new boolean[V]; // Rufen Sie die rekursive Hilfsfunktion auf, um // Topologische Sortierung ausgehend von allen Eckpunkten einzeln // nacheinander zu speichern for (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> Kanten = new ArrayList(); Kanten.add(Arrays.asList(0, 1)); Kanten.add(Arrays.asList(1, 2)); Kanten.add(Arrays.asList(3, 1)); Kanten.add(Arrays.asList(3, 2)); // Diagramm dargestellt als Adjazenzliste Liste> adj = new ArrayList(V); für (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : Kanten) { adj.get(i.get(0)).add(i.get(1)); } topologicalSort(adj, V); } }>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] besucht, Stack stack) { // Markiere den aktuellen Knoten als besucht besuchte[v] = true; // Wiederholung für alle benachbarten Scheitelpunkte foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, besuchte, stack); } // Aktuellen Scheitelpunkt in den Stapel verschieben, der das // Ergebnis speichert stack.Push(v); } // Funktion zum Durchführen einer topologischen Sortierung static void TopologicalSort(List> adj, int V) { // Stack zum Speichern des Ergebnisses Stack Stapel = neuer Stapel (); bool[] besuchte = new bool[V]; // Rufen Sie die rekursive Hilfsfunktion auf, um // Topologische Sortierung ausgehend von allen Eckpunkten einzeln // nacheinander zu speichern for (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Treibercode static void Main(string[] args) { // Anzahl der Knoten int V = 4; // Kantenliste> Kanten = neue Liste>{ neue Liste { 0, 1 }, neue Liste { 1, 2 }, neue Liste { 3, 1 }, neue Liste { 3, 2 } }; // Diagramm dargestellt als Adjazenzliste Liste> adj = neue Liste>(); für (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Liste i in Kanten) { adj[i[0]].Add(i[1]); } TopologicalSort(adj, V); } }>
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // Treibercode (() => { // Anzahl der Knoten const V = 4; // Kanten const Kanten = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Graph dargestellt als Adjazenzliste const adj = Array.from({ length: V }, () => []); (i[1]); } topologicalSort(adj, V})();> Ausgabe
Topological sorting of the graph: 3 0 1 2>
Zeitkomplexität: O(V+E). Der obige Algorithmus ist einfach DFS mit einem zusätzlichen Stapel. Die Zeitkomplexität ist also dieselbe wie bei DFS
Nebenraum: O(V). Der zusätzliche Platz wird für den Stapel benötigt
Topologische Sortierung mit BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Zeiger auf ein Array mit // Adjazenzlisten public: Graph(int V); // Konstruktor void addEdge(int v, int w); // Funktion zum Hinzufügen einer Kante zum Diagramm void topologicalSort(); // druckt eine topologische Sortierung // des vollständigen Diagramms }; Graph::Graph(int V) { this->V = V; adj = neue Liste [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // w zur Liste von v hinzufügen. } // Funktion zum Durchführen einer topologischen Sortierung void Graph::topologicalSort() { // Erstelle einen Vektor, um den In-Grad-Vektor aller Scheitelpunkte zu speichern in_degree(V, 0); // Adjazenzlisten durchqueren, um den Grad der // Eckpunkte auszufüllen für (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue Q; für (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Einer nach dem anderen Scheitelpunkte aus der Warteschlange entfernen und // benachbarte Scheitelpunkte in die Warteschlange einreihen, wenn der In-Grad des benachbarten Scheitelpunkts 0 wird, während (!q.empty()) { // Den Anfang der Warteschlange extrahieren (oder aus der Warteschlange entfernen) // und ihn hinzufügen topologische Ordnung int u = q.front(); q.pop(); top_order.push_back(u); // Alle Nachbarknoten // des aus der Warteschlange entfernten Knotens u durchlaufen und deren In-Grad // um 1 verringern ::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Wenn in-degree Null wird, füge es zur Warteschlange hinzu if (--in_degree[*itr ] == 0) q.push(*itr); count++; } // Prüfe, ob es einen Zyklus gab if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Adjazenzliste // Darstellung des // Graphen // Konstruktor Graph(int V) { this.V = V; adj = new ArrayList[V]; für (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = new LinkedList(); für (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = new ArrayList(); // Einer nach dem anderen Scheitelpunkte aus der Warteschlange entfernen und benachbarte Scheitelpunkte // in die Warteschlange einreihen, wenn der In-Grad von // angrenzend 0 wird, während (!q.isEmpty()) { // Vorderteil der Warteschlange extrahieren und zur // topologischen Reihenfolge hinzufügen int u = q.poll(); topOrder.add(u); count++; // Iteriere alle benachbarten Knoten des // aus der Warteschlange entfernten Knotens u und verringere deren In-Grad // um 1 for (int w : adj[u]) { // Wenn der In-Grad Null wird, füge ihn zur // Warteschlange hinzu if (--inDegree[w] == 0) q.add(w); } } // Prüfen, ob es einen Zyklus gab if (count != V) { System.out.println('Graph enthält Zyklus'); zurückkehren; } // Topologische Reihenfolge ausgeben for (int i : topOrder) System.out.print(i + ' '); } } // Treibercode public class Main { public static void main(String[] args) { // Einen im obigen Diagramm angegebenen Graphen erstellen Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Es folgt eine topologische Sortierung des angegebenen Diagramms'); g.topologicalSort(); } }> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Ausgabe
Following is a Topological Sort of the given graph 4 5 2 0 3 1>
Zeitkomplexität:
Die Zeitkomplexität für die Erstellung des Diagramms beträgt O(V + E), wobei V die Anzahl der Eckpunkte und E die Anzahl der Kanten ist.
Die Zeitkomplexität für die Durchführung der topologischen Sortierung mithilfe von BFS beträgt ebenfalls O(V + E), wobei V die Anzahl der Eckpunkte und E die Anzahl der Kanten ist. Dies liegt daran, dass jeder Scheitelpunkt und jede Kante während der BFS-Durchquerung einmal besucht wird.
Raumkomplexität:
Die räumliche Komplexität zum Speichern des Diagramms mithilfe einer Adjazenzliste beträgt O(V + E), wobei V die Anzahl der Eckpunkte und E die Anzahl der Kanten ist.
Zusätzlicher Platz wird zum Speichern des In-Grad-Werts der Scheitelpunkte verwendet, was O(V)-Platz erfordert.
Für die BFS-Durchquerung wird eine Warteschlange verwendet, die höchstens V Scheitelpunkte enthalten kann. Somit beträgt die Platzkomplexität für die Warteschlange O(V).
Insgesamt beträgt die räumliche Komplexität des Algorithmus aufgrund der Speicherung des Graphen, des In-Grade-Arrays und der Warteschlange O(V + E).
Zusammenfassend beträgt die zeitliche Komplexität der bereitgestellten Implementierung O(V + E) und die räumliche Komplexität beträgt ebenfalls O(V + E).
Notiz: Hier können wir anstelle des Stacks auch ein Array verwenden. Wenn das Array verwendet wird, drucken Sie die Elemente in umgekehrter Reihenfolge aus, um die topologische Sortierung zu erhalten.
Vorteile der topologischen Sortierung:
- Hilft bei der Planung von Aufgaben oder Ereignissen basierend auf Abhängigkeiten.
- Erkennt Zyklen in einem gerichteten Diagramm.
- Effizient zur Lösung von Problemen mit Prioritätsbeschränkungen.
Nachteile der topologischen Sortierung:
- Gilt nur für gerichtete azyklische Graphen (DAGs), nicht geeignet für zyklische Graphen.
- Möglicherweise nicht eindeutig, es können mehrere gültige topologische Ordnungen vorhanden sein.
- Ineffizient für große Diagramme mit vielen Knoten und Kanten.
Anwendungen der topologischen Sortierung:
- Aufgabenplanung und Projektmanagement.
- Abhängigkeitsauflösung in Paketverwaltungssystemen.
- Bestimmen der Kompilierungsreihenfolge in Software-Build-Systemen.
- Deadlock-Erkennung in Betriebssystemen.
- Kursplanung an Universitäten.
In Verbindung stehende Artikel:
- Kahns Algorithmus zur topologischen Sortierung
- Alle topologischen Arten eines gerichteten azyklischen Graphen