Das Volumen einer dreieckigen Pyramide wird mit der Formel ermittelt V = 1/3A.H . Eine dreieckige Pyramide, auch Tetraeder genannt, ist eine Pyramidenart mit einer dreieckigen Grundfläche und drei dreieckigen Flächen, die sich in einem einzigen Punkt, der Spitze, treffen.

In diesem Artikel lernen wir die Pyramidendefinition, die Dreieckspyramidendefinition, die Dreieckspyramidenformel, Beispiele und andere im Detail kennen.

Inhaltsverzeichnis

• Was ist eine Pyramide?
• Definition der dreieckigen Pyramide
• Dreieckige Pyramidenformel
• Oberfläche einer dreieckigen Pyramide
• Volumen einer dreieckigen Pyramide

Was ist eine Pyramide?

A Pyramide wird basierend auf der Form der Basis in verschiedene Arten eingeteilt, z. B. eine dreieckige Pyramide, eine quadratische Pyramide, eine fünfeckige Pyramide, eine sechseckige Pyramide usw. Eine Spitze ist ein Treffpunkt der Seitenflächen oder Seitenflächen einer Pyramide . Der senkrechte Abstand von der Spitze einer Pyramide zum Mittelpunkt ihrer Basis ist die Höhe oder Höhenlage einer Pyramide. Der senkrechte Abstand zwischen der Spitze und der Basis der Seitenflächenschräge einer Pyramide.

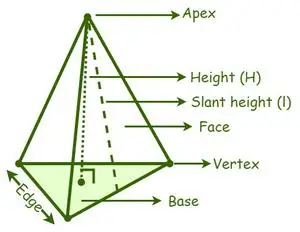
Pyramide

Definition der dreieckigen Pyramide

Dreieckige Pyramide ist eine Pyramide, deren Basis ein Dreieck ist. Es ist auch als Tetraeder bekannt und hat drei dreieckige Flächen und eine dreieckige Basis, wobei die dreieckige Basis skalar, gleichschenklig oder ein gleichseitiges Dreieck sein kann. Ein Dreieck wird weiter in drei Typen eingeteilt, nämlich eine regelmäßige dreieckige Pyramide, eine unregelmäßige dreieckige Pyramide und eine gerade dreieckige Pyramide.

• Regelmäßige dreieckige Pyramide: Eine dreieckige Pyramide, deren vier Flächen gleichseitige Dreiecke sind, wird als regelmäßige dreieckige Pyramide bezeichnet. Da die Pyramide aus gleichseitigen Dreiecken besteht, beträgt das Maß aller ihrer Innenwinkel 60°.

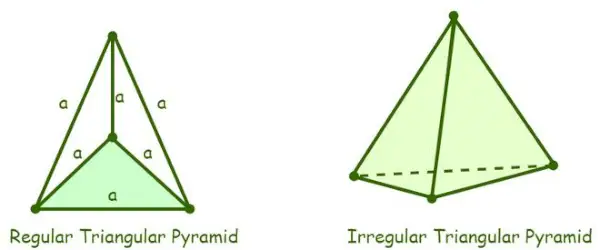
Definition der dreieckigen Pyramide

• Unregelmäßige dreieckige Pyramide: Eine unregelmäßige dreieckige Pyramide ist eine Pyramide, deren Kanten der Grundfläche nicht gleich sind, d. h. die Grundfläche einer unregelmäßigen dreieckigen Pyramide ist entweder ein ungleichseitiges Dreieck oder ein gleichschenkliges Dreieck. Bei allen dreieckigen Pyramiden wird davon ausgegangen, dass sie regelmäßig sind, es sei denn, eine dreieckige Pyramide wird ausdrücklich als unregelmäßig bezeichnet.

• Rechte Dreieckspyramide: Eine gerade dreieckige Pyramide ist eine Pyramide, deren Grundfläche ein rechtwinkliges Dreieck ist und deren Spitze über der Mitte der Grundfläche ausgerichtet ist.

Dreieckige Pyramidenformel

Für eine dreieckige Pyramide gibt es zwei Formeln: die Oberfläche einer dreieckigen Pyramide und das Volumen einer dreieckigen Pyramide.

String als Array

• Oberfläche einer dreieckigen Pyramide
  • Seitenfläche einer dreieckigen Pyramide
  • Gesamtoberfläche einer dreieckigen Pyramide
• Volumen einer dreieckigen Pyramide

Oberfläche einer dreieckigen Pyramide

Die Oberfläche einer Pyramide hat zwei Arten von Oberflächen, nämlich die Mantelfläche und die Gesamtoberfläche, wobei die Oberfläche einer Pyramide die Summe der Flächen der Mantelflächen oder Seitenflächen und der Grundfläche ist einer Pyramide.

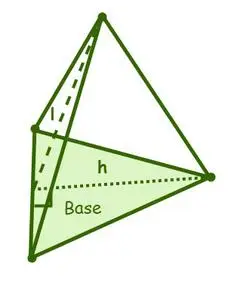
Oberfläche einer dreieckigen Pyramide

Seitenfläche einer dreieckigen Pyramide

Die Seitenfläche einer dreieckigen Pyramide wird nach folgender Formel berechnet:

Seitenfläche einer dreieckigen Pyramide (LSA) = ½ × Umfang × Neigungshöhe

Gesamtoberfläche einer dreieckigen Pyramide

Die Gesamtoberfläche einer Pyramide (TSA) = Seitenoberfläche der Pyramide + Grundfläche

Also, TSA = ½ × Umfang × Neigungshöhe + ½ × Basis × Höhe

Gesamtoberfläche einer dreieckigen Pyramide (TSA) = ½ × P × l + ½ bh

Wo,

• P ist der Umfang der Basis
• l ist die schräge Höhe der Pyramide
• B ist die Basis des Dreiecks an der Basis
• H ist die Höhe der Pyramide

Volumen einer dreieckigen Pyramide

Das Volumen einer Pyramide ist der gesamte Raum, der zwischen allen Flächen einer Pyramide eingeschlossen ist. Das Volumen einer Pyramide wird im Allgemeinen durch den Buchstaben V dargestellt und seine Formel entspricht einem Drittel des Produkts aus Grundfläche und Höhe der Pyramide.

Die Formel für das Volumen einer Pyramide lautet wie folgt:

Volumen einer dreieckigen Pyramide = 1/3 × Grundfläche × Höhe

V = 1/3 × AH Kubikeinheiten

Wo,

• IN ist das Volumen der Pyramide
• A ist die Grundfläche einer Pyramide
• H ist Höhe oder Höhe einer Pyramide

Die Formel für das Volumen einer regelmäßigen dreieckigen Pyramide lautet wie folgt

Volumen der regelmäßigen dreieckigen Pyramide = a ³ /6√2 Kubikeinheiten

Wo A isLength der Kanten

Artikel zur Dreieckspyramide:

• Rechteckige Pyramide
• Quadratische Pyramide
• Fünfeckige Pyramide
• Sechseckige Pyramide
• Volumen einer Pyramidenformel
• Oberfläche einer Pyramidenformel

Beispiele zur Dreieckspyramidenformel

Beispiel 1: Bestimmen Sie das Volumen einer dreieckigen Pyramide, deren Grundfläche und Höhe 50 cm betragen ² bzw. 12 cm.

Lösung:

Gegebene Daten,

• Fläche der dreieckigen Grundfläche = 100 cm²
• Höhe der Pyramide = 12 cm

Wir wissen das,

Volumen einer dreieckigen Pyramide (V) = 1/3 × Fläche der dreieckigen Grundfläche × Höhe

H = 1/3 × 50 × 12 = 200 cm³

Daher beträgt das Volumen der gegebenen dreieckigen Pyramide 200 cm³.

Beispiel 2: Ermitteln Sie die Gesamtoberfläche einer regelmäßigen dreieckigen Pyramide, wenn die Länge jeder Kante 8 Zoll beträgt.

Lösung:

Gegebene Daten,

Mission Impossible alle Filme

• Länge jeder Kante einer regelmäßigen dreieckigen Pyramide (a) = 8 Zoll

Wir wissen das,

Gesamtoberfläche einer regelmäßigen dreieckigen Pyramide = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110,851 Quadratzoll

Daher beträgt die Gesamtoberfläche einer regelmäßigen dreieckigen Pyramide 110,851 Quadratzoll.

Beispiel 3: Bestimmen Sie das Volumen einer regelmäßigen dreieckigen Pyramide, wenn die Kantenlänge 10 cm beträgt.

Lösung:

Gegebene Daten,

• Länge jeder Kante einer regelmäßigen dreieckigen Pyramide (a) = 10 cm

Wir wissen das,

Volumen einer regelmäßigen dreieckigen Pyramide = a³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 cm³

Daher beträgt das Volumen einer regelmäßigen dreieckigen Pyramide 117,85 Kubikmeter. cm.

Beispiel 4: Ermitteln Sie die Neigungshöhe der dreieckigen Pyramide, wenn ihre Mantelfläche 600 Quadratzoll und der Umfang der Basis 60 Zoll beträgt.

Lösung:

Gegebene Daten,

• Seitenfläche = 600 Quadratzoll
• Umfang der Basis = 60 Zoll

Wir wissen das,

Hallo Welt Java

Seitenfläche = ½ × Umfang × Neigungshöhe

600 = ½ × 60 × l

l = 600/30 = 20 Zoll

Daher beträgt die Schräghöhe der gegebenen Pyramide 20 Zoll.

Beispiel 5: Bestimmen Sie die Gesamtoberfläche einer dreieckigen Pyramide, deren Grundfläche 28 cm² beträgt, deren Umfang 18 cm beträgt und deren Neigungshöhe 20 cm beträgt.

Lösung:

Gegebene Daten,

• Fläche der dreieckigen Basis = 28 cm²
• Schräghöhe (l) = 20 cm
• Umfang (P) = 18 cm

Wir wissen das,

Gesamtoberfläche (TSA) einer dreieckigen Pyramide = ½ × Umfang × Neigungshöhe + Grundfläche

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 cm²

Somit beträgt die Gesamtoberfläche der gegebenen Pyramide 208 cm².

Üben Sie Aufgaben zur Dreieckspyramidenformel

Q1. Wie groß ist das Volumen einer dreieckigen Pyramide mit einer Grundfläche von 15 Quadrateinheiten und einer Höhe von 10 Einheiten?

Q2. Wie groß ist die Gesamtoberfläche der Pyramide bei einer regelmäßigen dreieckigen Pyramide, bei der jede Kante der gleichseitigen dreieckigen Grundfläche 6 Einheiten misst?

Q3. Wie groß sind bei einer regelmäßigen dreieckigen Pyramide, bei der jede Kante der gleichseitigen dreieckigen Grundfläche 4 Einheiten misst und die Höhe 5 Einheiten beträgt, das Volumen und die Gesamtoberfläche der Pyramide?

Q4. Wenn die Seitenlängen der Basis einer dreieckigen Pyramide 3 Einheiten, 4 Einheiten und 5 Einheiten betragen und die Höhe der Pyramide 12 Einheiten beträgt, wie groß ist dann das Volumen der Pyramide?

F5. Wie groß ist die Gesamtoberfläche einer dreieckigen Pyramide mit einer Basis in Form eines rechtwinkligen Dreiecks mit Beinen von 3 und 4 Einheiten und einer Hypotenuse von 5 Einheiten, wenn die Höhe der Pyramide von der Basis bis zur Spitze 10 Einheiten beträgt? ?

FAQs zur Dreieckspyramidenformel

Was ist die Definition einer dreieckigen Pyramide?

Eine dreieckige Pyramide ist eine geometrische Form mit einer dreieckigen Grundfläche und drei dreieckigen Flächen mit einer gemeinsamen Spitze.

Wie viele Flächen und Eckpunkte hat eine dreieckige Pyramide?

Die dreieckige Pyramide hat vier Flächen und vier Spitzen. Ein Scheitelpunkt ist allen drei Flächen der Pyramide gemeinsam.

Was ist die Grundformel für eine Pyramide?

Grundformeln einer Pyramide sind:

• LSA = ½ × Umfang × Neigungshöhe
• TSA = ½ × P × l + ½ bh
• V = 1/3 × AH

Welche Arten von Dreieckspyramiden gibt es?

Es gibt drei Arten von dreieckigen Pyramiden

• Regelmäßige dreieckige Pyramide
• Unregelmäßige dreieckige Pyramide
• Rechtwinklige dreieckige Pyramide

Was ist die Formel für Dreiecke?

Die Formel für die Fläche eines Dreiecks lautet:

• (Fläche)A = 1/2 × b × h