Nullstellen eines Polynoms Sind das reale, imaginäre oder komplexe Werte, wenn man sie anstelle einer Variablen in das Polynom einfügt, wird das Ergebnis Null (wie der Name auch Null andeutet). Polynome werden verwendet, um einige physikalische Phänomene im wirklichen Leben zu modellieren. Sie sind sehr nützlich, um Situationen mathematisch zu beschreiben.

Die Nullstellen eines Polynoms sind alle x-Werte, die das Polynom gleich Null machen. Nullstellen eines Polynoms sagen uns etwas über die x-Achsenabschnitte des Graphen des Polynoms. In diesem Artikel werden wir darüber diskutieren Nullstellen eines Polynoms, wie man sie findet, den Faktorsatz usw.

Inhaltsverzeichnis

• Was sind Nullstellen von Polynomen?
• Nullstellen der Polynomformel
• Wie finde ich den Nullpunkt eines Polynoms?
• Für lineares Polynom
• Für quadratisches Polynom
• Für kubisches Polynom
• Faktorsatz
• Beziehung zwischen Nullstellen und Koeffizienten
• Beziehung zwischen Nullstellen und Koeffizienten für quadratische Gleichungen
• Beziehung zwischen Nullstellen und Koeffizienten für die kubische Gleichung
• Bilden einer Gleichung mit Nullstellen eines Polynoms
• Nullstellen im Polynomgraphen
• Grundsatz der linearen Algebra
• Multiplizität einer Wurzel
• Artikel zum Thema Nullstellen von Polynomen
• Beispielaufgaben zu Nullstellen von Polynomen
• Übungsaufgaben zu Nullstellen von Polynomen

Was sind Nullstellen von Polynomen?

Für ein Polynom P(x) sagen wir, dass x = a die Nullstelle des Polynoms ist, wenn P(a) = 0, und alle solchen Nullstellen eines Polynoms werden üblicherweise Nullstellen eines Polynoms genannt. Betrachten Sie zum Beispiel f(x) = 3x – 12. Setzen Sie nun x = 4 in das Polynom ein, d. h. f(4) = 3×4 – 12 = 0. Somit ist x = 4 eine Nullstelle des Polynoms f( x) = 3x – 12.

Beispiel: Für f(x) = x ³ – 6x ² + 11x – 6, ist x = 1 Null?

Lösung:

Um zu überprüfen, ob x = 1 Null von f(x) = x ist³– 6x²+ 11x – 6 oder nicht, setze x = 1 in (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Somit ist x = 1 eine Nullstelle von f(x).

Nullstellen der Polynomformel

Für ein lineares Polynom der Form ax + b ist sein Nullpunkt durch x = -b/a gegeben.

Für ein quadratisches Polynom der Form ax²+ bx + c, sein Nullpunkt ist durch x = {- b ± √D}/2a gegeben, wobei D die durch b gegebene Diskriminante ist²– 4ac.

Wie finde ich den Nullpunkt eines Polynoms?

Mit verschiedenen Methoden, die im Folgenden erläutert werden, können wir die Nullstellen des Polynoms für verschiedene Arten von Polynomen ermitteln.

• Für lineares Polynom
• Für quadratisches Polynom
• Für kubisches Polynom

Für lineares Polynom

Bei linearen Polynomen ist es am einfachsten, Null zu finden. da es nur eine Nullstelle gibt und diese auch durch einfache Umordnung des Polynoms nach dem gleichsetzenden Polynom auf 0 berechnet werden kann.

Finden Sie beispielsweise Null für das lineare Polynom f(x) = 2x – 7.

Lösung:

Um den Nullpunkt von f(x) zu finden, setzen Sie f(x) mit 0 gleich.

⇒ 2x – 7 = 0

⇒ 2x = 7

NPM-Cache leer

⇒ x = 7/2

Für quadratisches Polynom

Es gibt verschiedene Methoden, um Wurzeln oder Nullstellen eines quadratischen Polynoms zu finden, z. B. das Teilen des Mittelterms, eine quadratische Formel, die auch als Shree-Dharacharya-Formel bekannt ist, und das Vervollständigen des Quadrats, das der quadratischen Formel, wie sie auch als quadratische Formel bezeichnet wird, etwas ähnelt aus der Vervollständigung des Quadrats für die allgemeine quadratische Gleichung.

Lerne mehr über Lösen quadratischer Gleichungen oder Polynome und wie man sie löst. Die folgenden Beispiele zeigen die Methode zum Finden von Nullstellen quadratischer Polynome im Detail.

Beispiel 1: Finden Sie die Nullstellen für P(x) = x heraus ² + 2x – 15.

Antwort:

X²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Beispiel 2: Finden Sie die Nullstellen für P(x) = x ² – 16x + 64.

Antwort:

X²– 16x + 64 = 0

Vergleich mit Axt²+ bx + c = 0,

wir erhalten a = 1, b = -16 und c = 64.

Daher,

⇒ x = 8, 8

Für kubisches Polynom

Es gibt viele Möglichkeiten, kubische Nullstellen zu finden, beispielsweise den Rational-Wurzel-Satz und die lange Division zusammen. Eine Methode, Wurzeln von kubischen Polynomen oder Polynomen höheren Grades zu finden, ist wie folgt:

Schritt 1: Verwenden Sie den rationalen Wurzelsatz, um die möglichen Wurzeln zu finden. Das heißt, wenn ein Polynom eine rationale Wurzel hat, muss es die Division von p/q sein, wobei p die ganzzahlige Konstante und q der führende Koeffizient ist.

Schritt 2: Nachdem Sie eine Wurzel gefunden haben, dividieren Sie das Polynom durch den durch diese Wurzel gebildeten Faktor, indem Sie eine lange Division durchführen, und schreiben Sie das Polynom als Produkt aus Quotient und Dividende.

Schritt 3: Wenn der Quotient ein quadratischer Ausdruck ist, lösen Sie ihn mit den oben genannten Methoden für quadratische Polynome. Wenn es sich nicht um ein Polynom vom Grad 2 handelt, wiederholen Sie die Schritte 1 und 2, bis der Quotient ein Polynom vom Grad 2 wird.

Schritt 4: Das Ergebnis von Schritt 3 sind die erforderlichen Faktoren. Indem wir den Faktor mit 0 gleichsetzen, können wir die Nullstellen des Polynoms ermitteln.

Beispiel: Finden Sie die Nullstellen des kubischen Polynoms p(x) = x ³ + 2x ² – 5x – 6.

Lösung:

p(x) = x³+ 2x²– 5x – 6

Als p/q = -6

Nach dem Rational-Wurzel-Theorem sind alle möglichen rationalen Wurzeln des Polunomials Teiler von p/q.

Somit sind Teiler = ±1, ±2, ±3, ±6

x = -1, in p(x), erhalten wir

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Nach dem Faktorsatz ist x + 1 also der Faktor von p(x).

Also x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Für Nullen gilt p(x) = 0,

Nullstellen von p(x) sind x = -1, x = 2 und x = -3.

Faktorsatz

Für das Polynom P(x) besagt der Faktorsatz, dass, wenn x =a Null von P(X) ist, genau dann gilt, wenn x – a ein Faktor von P(x) ist. d. h. die beiden folgenden Bedingungen sollten zutreffen.

• Wenn a eine Nullstelle von P(x) ist, dann ist x−a ein Faktor von P(x).
• Wenn x−a ein Faktor von P(x) ist, dann ist a eine Nullstelle von P(x)

Dies kann anhand früherer Beispiele überprüft werden. Der Faktorsatz kann zu einigen interessanten Ergebnissen führen, die wie folgt lauten:

Ergebnis 1: Wenn P(x) ein Polynom vom Grad n ist und r eine Nullstelle von P(x) ist, dann kann P(x) in der folgenden Form geschrieben werden:

P(x) = (x – r) Q(x)

Wobei Q(x) ein Polynom vom Grad n-1 ist und durch Division von P(x) durch (x – r) ermittelt werden kann.

Ergebnis 2: Wenn P(x) = (x-r)Q(x) und x = t eine Nullstelle von Q(x) ist, dann ist x = t auch eine Nullstelle von P(x).

Um die obige Tatsache zu überprüfen,

Nehmen wir an, t ist Null Q(x), was bedeutet, dass Q(t) = 0.

Wir wissen, dass r eine Nullstelle des Polynoms P(x) ist, wobei P(x) = (x – r) Q(x),

Wir müssen also prüfen, ob x = t auch eine Nullstelle von P(x) ist. Setzen wir x = t in P(x)

⇒ P(t) = (t – r) Q(t) = 0

Also ist x = t auch eine Nullstelle P(x).

Daher bewiesen.

Beziehung zwischen Nullstellen und Koeffizienten

Die Beziehung zwischen den Nullstellen und dem Koeffizienten der quadratischen und kubischen Gleichung wird unten diskutiert.

Beziehung zwischen Nullstellen und Koeffizienten für quadratische Gleichungen

Für eine quadratische Gleichung der Form ax²+ bx + c = 0, wenn die beiden Nullstellen der quadratischen Gleichung α und β sind, dann

• Summe der Wurzel = α + β = -b/a
• Produkt der Wurzeln = α × β = c/a

Beziehung zwischen Nullstellen und Koeffizienten für die kubische Gleichung

Wenn α, β und γ die Wurzel des kubischen Polynoms ax sind³+ bx²+ cx + d = 0, dann ist die Beziehung zwischen seinen Nullstellen und Koeffizienten wie folgt gegeben:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Bilden einer Gleichung mit Nullstellen eines Polynoms

• Für ein quadratisches Polynom mit Nullstellen α und β ist das quadratische Polynom gegeben durch

X ² – (a + b)x + ab .

• Für ein kubisches Polynom mit drei Nullstellen α, β und γ ist das kubische Polynom gegeben durch

X ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

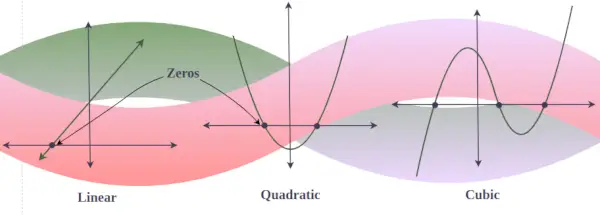
Nullstellen im Polynomgraphen

Im Graphen eines beliebigen Polynoms y = f(x) sind reelle Nullstellen der Punkt, an dem der Graph die x-Achse schneidet oder berührt. (da ein Graph mit einer imaginären Null niemals die x-Achse schneidet). Mit anderen Worten: Wenn es drei reelle Lösungen eines kubischen Polynoms gibt, schneidet der Graph dieses kubischen Polynoms die x-Achse dreimal. Wenn es jedoch nur eine reelle Lösung für ein kubisches Polynom gibt, schneidet der Graph nur die x-Achse einmal.

Grundsatz der linearen Algebra

Wenn P(x) ein Polynom vom Grad n ist, dann hat P(x) genau n Nullstellen, von denen sich einige wiederholen können.

Das heißt, wenn wir alle Nullen auflisten und jede einzelne k-mal auflisten, wobei k ihre Multiplizität ist. Wir werden genau n Zahlen in der Liste haben. Dies kann nützlich sein, da es uns eine Vorstellung davon geben kann, wie viele Nullstellen ein Polynom enthalten sollte. Wir können also aufhören, nach Nullen zu suchen, sobald wir die erforderliche Anzahl an Nullen erreicht haben.

Multiplizität einer Wurzel

Angenommen, wir haben ein Polynom P(x) = 0, das faktorisiert wird in:

P(x) = (x – r) ^k (x – a) ^M

Sanjay Dutt und

Wenn r eine Nullstelle eines Polynoms ist und der Exponent seines Termes, der die Wurzel erzeugt hat, k ist, dann sagen wir, dass r hat Multiplizität k . Oft werden Nullen mit einer Multiplizität von 1 genannt einfach Nullstellen und Nullstellen mit einer Multiplizität von 2 werden Doppelwurzeln des Polynoms genannt.

Beispiel: P(x) ist ein Polynom vom Grad 5, das für Sie faktorisiert wurde. Listen Sie die Wurzeln und ihre Vielfältigkeit auf.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x−2) ³

Lösung:

Gegeben sei P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Um Nullstellen zu finden, ist P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Beachten Sie, dass -1 zweimal als Null vorkommt, daher ist seine Multiplizität 2, während die Multiplizität der Null 2 ​​3 ist.

Artikel zum Thema Nullstellen von Polynomen

• Polynom
• Wurzeln der quadratischen Gleichung
• Algebraischer Ausdruck

Beispielaufgaben zu Nullstellen von Polynomen

Problem 1: Vorausgesetzt, dass x = 2 eine Nullstelle von P(x) = x ist ³ +2x ² −5x−6. Finden Sie die anderen beiden Nullen.

Lösung:

Aus dem Grundsatz, den wir zuvor untersucht haben, können wir sagen, dass P(x) drei Nullstellen haben wird, weil es ein Polynom dritten Grades ist. Einer davon ist x = 2.

Also können wir P(x) umschreiben,

P(x) = (x – 2) Q(x)

Um die anderen beiden Nullstellen zu finden, müssen wir Q(x) ermitteln.

Q(x) kann durch Division von P(x) durch (x-2) ermittelt werden.

Nach der Division ergibt sich für Q(x)

Q(x) = x²+ 4x + 3

Daraus lassen sich die restlichen zwei Nullstellen ermitteln,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Somit sind die anderen beiden Nullstellen x = -1 und x = -3.

Aufgabe 2: Vorausgesetzt, dass x = r eine Nullstelle eines Polynoms ist, finden Sie die anderen Nullstellen des Polynoms heraus.

P(x) = x ³ -6x ² −16x; r = −2

Lösung:

Wir wissen, dass x = -2 eine Null ist,

P(x) kann also umgeschrieben werden als: P(x) = (x + 2) Q(x) {Durch Verwendung des Divisionsalgorithmus}

Um nun Q(x) zu finden, machen wir dasselbe wie in der vorherigen Frage, wir dividieren P(x) durch (x + 2).

Wir bekommen,

Q(x) = x²– 8x

Um nun die anderen beiden Nullstellen zu finden, faktorisieren Sie Q(x)

Q(x) = x (x – 8) = 0

Die Nullstellen sind also x = 0, 8.

Somit haben wir drei Nullen, x = -2, 0, 8.

Aufgabe 3: Finden Sie die Nullstellen des Polynoms 4x ³ -3x ² -25x-6 = 0

Lösung:

Trick, um Polynomgleichungen mit Grad 3 zu lösen,

Finden Sie die kleinste ganze Zahl, die den Polynomwert 0 ergeben kann, beginnen Sie mit 1, -1,2 usw.

Wir finden, dass für x = -2 der Wert von expression Null ist.

setinterval Javascript

Daher ist eine der Wurzeln -2.

Gemäß dem Faktorsatz ist (x-a) der Faktor eines gegebenen Polynoms, wenn a eine der Nullstellen des Polynoms ist.

Somit ist {x – (-2)} = (x+2) ein Faktor pof über dem Polynom.

Wir erhalten eine quadratische Gleichung und eine Nullstelle ist bereits vorhanden.

(4x²-11x-3)(x+2) = 0

Faktorisieren Sie die quadratische Gleichung,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Aufgabe 4: Finden Sie die Nullstellen des Polynoms 4x ⁶ – 16x ⁴ = 0

Lösung:

Das Polynom hat bis zu Grad 6, daher gibt es 6 Nullstellen des Polynoms.

4x⁴(X²-4) = 0

4x⁴(X²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Daher ist x= 0, 0, 0, 0, 2, -2

Aufgabe 5: Finden Sie die Nullstellen der Polynomfunktion f(x) = x ³ – 2x ² – 5x + 6

Lösung:

Um die Nullstellen dieses Polynoms zu finden, setzen wir f(x) = 0 und lösen nach x auf:

f(x) = x³– 2x²– 5x + 6 = 0

Da d/a = 6

Nach dem Rationalwurzelsatz sind alle möglichen rationalen Wurzeln des Polunomial:

Teiler von d/a = ±1, ±2, ±3, ±6

x = 1, in p(x), erhalten wir

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

javafx

Nach dem Faktorsatz ist x – 1 also der Faktor von p(x).

Also x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

X³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Für Nullen gilt p(x) = 0,

Nullstellen von p(x) sind x = 1, x = -2 und x = 3.

Übungsaufgaben zu Nullstellen von Polynomen

1. Finden Sie alle Nullstellen des Polynoms f(x) = x ³ – 6x ² + 11x – 6

2. Bestimmen Sie alle Nullstellen des Polynoms g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Finden Sie die Nullstellen des Polynoms h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Bestimmen Sie alle Nullstellen des Polynoms p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

FAQs zu Nullstellen von Polynomen

Was sind Nullstellen eines Polynoms?

Solche realen Werte, denn der Wert des Polynoms wird 0, d. h. wenn p(x) ein Polynom ist und p(a) = 0, dann ist x = a die Nullstelle von p(x).

Wie finde ich die Nullstellen eines Polynoms?

Es gibt verschiedene Methoden für verschiedene Polynome, um Nullstellen zu finden, z. B. für das quadratische Verschütten des Mittelterms und die quadratische Formel. Für lineare, einfache Umordnungen von Variablen und für kubische verwenden wir eine Kombination aus rationalem Wurzelsatz, langer Division, Faktorsatz und Restsatz.

Kann ein Polynom mehr als eine Null haben?

Ja, ein Polynom kann mehr als eine Nullstelle haben, tatsächlich kann das Polynom von n Graden höchstens n reelle Nullstellen haben.

Was ist die Multiplizität einer Nullstelle eines Polynoms?

Beim Faktorisierungsprozess kam ein Faktor oder eine Nullstelle eines Polynoms dann so oft vor, wie oft ein Faktor oder eine Nullstelle vorkam, das nennt man die Multiplizität dieser Wurzel.

Was ist der Fundamentalsatz der Algebra?

Der Grundsatz der Algebra besagt: Wenn P(x) ein Polynom vom Grad n ist, dann hat P(x) genau n Nullstellen, von denen sich einige wiederholen können.

Hat ein Polynom mit Grad n immer n reelle Wurzeln?

Nein, ein Polynom mit Grad n hat nicht immer n reelle Wurzeln, da einige Wurzeln imaginäre oder komplexe Zahlen sein können.

Was ist der Grad des Nullpolynoms?

Der Grad des Nullpolynoms ist Null.