- Der bitweise XOR-Operator ist auch als bekannt Exklusiv oder
- Es wird mit dem gekennzeichnet '^'
- Wie der Name schon sagt, funktioniert es auf der Bitebene der Operanden.
- Der bitweise XOR-Operator gehört zur Kategorie der bitweisen Operatoren.
- Beim bitweisen Exklusiv-ODER-Operator (XOR) sind zwei Operanden erforderlich, und diese beiden Operanden werden durch das XOR-Symbol, d. h. „^“, getrennt.
- Um die Ausgabe oder das Ergebnis zu bestimmen, das nach der Anwendung des XOR-Operators auf zwei Operanden ausgegeben wird, müssen wir der logischen Wahrheitstabelle des XOR-Operators folgen.
- Die XOR-Wahrheitstabelle ist die mathematische Tabelle, die unter Verwendung der richtigen Logik des XOR-Operators erstellt wurde.
- Die hinter dem XOR-Operator verwendete Logik ist; immer dann, wenn eine XOR-Operation auf die beiden angewendet wird anders Bits von zwei Operanden, dann wird das Ergebnis immer erzeugt '1', und wenn die XOR-Operation auf die beiden angewendet wird Dasselbe Bits von zwei Operanden, dann erzeugt das Ergebnis eine Ausgabe '0'.
Wahrheitstabelle des Exklusiv-ODER-Operators (XOR).
Es seien zwei Operanden vorhanden; der erste ist A und der zweite ist B, die Gesamtkombination der durch diese beiden Operanden gebildeten Eingaben beträgt 4. Mithilfe der folgenden XOR-Wahrheitstabelle bestimmen wir die entsprechende Ausgabe. Das Ergebnis wird hier in C erfasst C = A ^ B.
In dieser Wahrheitstabelle nehmen wir die Eingabe in Form von Bits entgegen, d. h. 0 und 1, und die Ausgabe wird ebenfalls in Form von Bits generiert, d. h. 0 und 1.
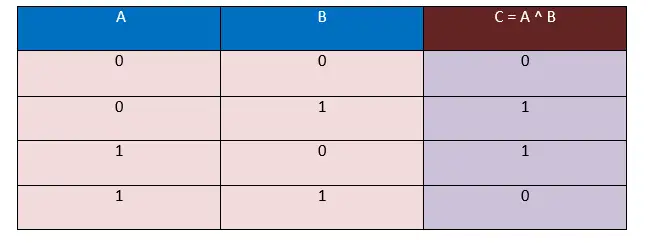
Hier, in der obigen XOR-Wahrheitstabelle, beobachten wir, dass das Ergebnis immer 1 ist, wenn die Werte der Operanden A und B unterschiedlich sind, d. h. ( 0, 1 ), ( 1, 0 ). Wenn die Werte der Operanden A und B gleich sind, d. h. ( 0, 0 ), ( 1, 1 ), wird das Ergebnis immer 0 sein.
Ebenso können wir auf diese Weise die Wahrheitstabelle für zeichnen Boolescher Wert Werte -
Es seien zwei Operanden vorhanden; der erste ist A und der zweite ist B . Die Gesamtkombination der durch diese beiden Operanden gebildeten Eingaben beträgt 4. Mithilfe der folgenden XOR-Wahrheitstabelle ermitteln wir die entsprechende Ausgabe. Das Ergebnis wird in C erfasst, hier C = A ^ B.
In dieser Wahrheitstabelle nehmen wir Eingaben in Form von Wahrheitswerten entgegen, d. h. Wahr (T) und Falsch (F). Die Ausgabe wird auch in Form von True-Werten generiert, d. h. T und F.

Hier, in der obigen XOR-Wahrheitstabelle, beobachten wir, dass das Ergebnis immer T ist, wenn die Werte der Operanden A und B unterschiedlich sind, d. h. (F, T), (T, F). Die Werte der Operanden A und B sind gleich, d. h. (F, F), (T, T), das Ergebnis ist immer F.
Aus den obigen Tabellen können wir das erkennen T (Wahr) wird mit eins und F (Falsch) mit 0 bezeichnet.
Schritte zur Lösung eines bestimmten Problems -
- Die in der Aufgabe angegebenen Operanden liegen immer im Dezimalwert vor.
- Zuerst müssen wir die Werte der Operanden in umwandeln binär
- Nachdem Sie die Werte der Operanden in Binärzahlen umgewandelt haben, legen Sie beide Operanden übereinander.
- Denken Sie daran, dass Sie vor der Anwendung der Exklusiv-ODER-Operation (XOR) Folgendes überprüfen sollten Anzahl an Ziffern in ihnen.
- Wenn die Anzahl der Ziffern nicht übereinstimmt, gleichen die zusätzlichen Nullen am linken Ende des kleinen Operanden die Anzahl der Ziffern aus.
- Wenden Sie abschließend mit Hilfe der obigen Wahrheitstabelle die XOR-Operation nacheinander auf die Operanden an, wobei Sie jeweils ein Bit für die Anwendung der XOR-Operation verwenden.
- Schließlich wird das Ergebnis in Form einer Ausgabe erzeugt.
- Die erzeugte Ausgabe erfolgt in binärer Form. Konvertieren Sie nun die binäre Form in eine dezimale Form und notieren Sie den Ergebniswert.
Ausführung einer bitweisen exklusiven ODER-Operation (XOR) in C++
Lassen Sie uns anhand von Beispielen die Ausführung der XOR-Operation in C++ genauer verstehen -
Beispiel 1: Finden Sie das Exklusiv-ODER von ganzzahligen Werten; 10 und 14. Erklären Sie es außerdem und schreiben Sie den Ausführungscode in C++.
Lösung: Betrachten wir zwei Variablen „a“ und „b“, um die entsprechenden beiden in der obigen Frage angegebenen Operanden zu speichern, d. h. 10 und 14.
Hier ist a = 10 und b = 14.
Wir werden die folgenden Schritte ausführen, um das Exklusiv-ODER der beiden angegebenen Operanden herauszufinden.
- Wir wissen, dass 10 und 14 in Dezimalform vorliegen, und um die bitweise XOR-Operation anzuwenden, ist es notwendig, sie in Binärform umzuwandeln.
- Binärform „a“, also 10 is '1010' und Binärform von 'b', d. h. 14 ist '1110'.
- Hier beobachten wir, dass die Anzahl der in a vorhandenen Binärziffern vier beträgt und die Anzahl der in b vorhandenen Binärziffern ebenfalls 4 beträgt; Daher ist die Anzahl der in beiden Variablen vorhandenen Binärziffern gleich und bereits ausgeglichen. Wir müssen nicht noch mehr Nullen hinzufügen, um das Gleichgewicht herzustellen.
- Nun werden die in „b“ vorhandenen Binärziffern auf die in „a“ vorhandenen Binärziffern reduziert.
- Abschließend wenden Sie die XOR-Operation nacheinander auf die entsprechenden Bitübereinstimmungen an und notieren die Ausgabe.
- Die zuletzt generierte Ausgabe erfolgt in binärer Form, da die obige Frage in Dezimalform angegeben wurde. Daher müssen wir das Ergebnis in Dezimalform umwandeln.
Erläuterung:
a = 10 (in Dezimalform)
Was ist Ruhezustand in Java?
b = 14 (in Dezimalform)
Für ein XOR b müssen wir nun a und b in binäre Form umwandeln –
a = 1010 (in binärer Form)
b = 1110 (in binärer Form)
Wenden wir nun die XOR-Operation auf a und b an –
a = 1010
b = 1110
---------------
a ^ b = 0100 (In binärer Form)
Das Ergebnis von a ^ b ist 0100, was in binärer Form vorliegt.
Konvertieren Sie nun das Ergebnis in Dezimalform, also 4.
10^14 = 4
HINWEIS: Durch die Verwendung der obigen XOR-Wahrheitstabelle wird die Ausgabe entsprechender Bits generiert.
Wir wenden nun die bitweise XOR-Operation auf 10 und 14 in der Sprache C++ an und erhalten das Ergebnis, d. h. 4.
C++-Code für das obige Beispiel:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Ausgabe
String-Verkettung Java

Beispiel 2: Finden Sie das Exklusiv-ODER von ganzzahligen Werten; 3 und 15. Erklären Sie es außerdem und schreiben Sie den Ausführungscode in C++.
Lösung: Betrachten wir zwei Variablen „a“ und „b“, um die entsprechenden beiden in der obigen Frage angegebenen Operanden zu speichern, d. h. 3 und 15.
Hier ist a = 3 und b = 15.
Wir werden die folgenden Schritte ausführen, um das Exklusiv-ODER der beiden angegebenen Operanden herauszufinden.
- Wir wissen, dass 3 und 15 in Dezimalform vorliegen, und um die bitweise XOR-Operation anzuwenden, ist es notwendig, sie in Binärform umzuwandeln.
- Binärform 'a', also 3 ist 'elf' und Binärform von 'b', d. h. 15 ist '1111'.
- Hier werden wir beobachten, dass die Anzahl der in a vorhandenen Binärziffern zwei und die Anzahl der in b vorhandenen Binärziffern vier beträgt; Daher ist die Anzahl der in beiden Variablen vorhandenen Binärziffern nicht gleich. Daher müssen wir im unausgeglichenen Zustand mehr Nullen auf der linken Seite der unteren Binärzahl hinzufügen, d. h. a, was „ elf' , um es auszugleichen.
- Nach dem Ausgleich beträgt der Wert von a '0011' , und b ist '1111'.
- Nun werden die in „b“ vorhandenen Binärziffern auf die in „a“ vorhandenen Binärziffern reduziert.
- Abschließend wenden Sie die XOR-Operation nacheinander auf die entsprechenden Bitübereinstimmungen an und notieren die Ausgabe.
- Die zuletzt generierte Ausgabe erfolgt in binärer Form, da die obige Frage in Dezimalform angegeben wurde. Daher müssen wir das Ergebnis in Dezimalform umwandeln.
Erläuterung:
a = 3 (in Dezimalform)
b = 15 (in Dezimalform)
Für ein XOR b müssen wir nun a und b in binäre Form umwandeln –
a = 0011 (in binärer Form)
b = 1111 (in binärer Form)
Wenden wir nun die XOR-Operation auf a und b an –
a = 0011
b = 1111
---------------
a ^ b = 1100 (In binärer Form)
Das Ergebnis von a ^ b ist 1100, was in binärer Form vorliegt.
Konvertieren Sie nun das Ergebnis in Dezimalform, also 12.
if else-Anweisung Java
3^15 = 12
HINWEIS: Durch die Verwendung der obigen XOR-Wahrheitstabelle wird die Ausgabe entsprechender Bits generiert.
Wir wenden nun die bitweise XOR-Operation auf 3 und 15 in der Sprache C++ an und erhalten das Ergebnis, d. h. 12.
C++-Code für das obige Beispiel:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Ausgabe

