Die Kartenwahrscheinlichkeit ist die Wahrscheinlichkeit der Ereignisse, an denen ein Spielkartenspiel beteiligt ist. Wie wir wissen, ist die Wahrscheinlichkeit eines der wichtigsten Themen der Mathematik, die sich mit der Berechnung der Möglichkeit eines Ereignisses befasst. In einfachen Worten ist die Kartenwahrscheinlichkeit ein Teil der Wahrscheinlichkeit, in dem wir die Wahrscheinlichkeit angeben, eine Karte aus dem Kartenspiel zu ziehen. In diesem Artikel lernen wir die Kartenwahrscheinlichkeit kennen, mit allen Einzelheiten zum Kartenwahrscheinlichkeitsdiagramm, zur Spielkartenwahrscheinlichkeit, zum Ermitteln der Kartenwahrscheinlichkeit und gelösten Beispielen für die Kartenwahrscheinlichkeit. Beginnen wir mit dem Lernen zum Thema Kartenwahrscheinlichkeit.
Was ist Wahrscheinlichkeit?
Wahrscheinlichkeit ist der Zweig der Mathematik, der die Möglichkeiten untersucht, ob ein Ereignis eintritt oder nicht. Mathematisch ist es nichts anderes als das Verhältnis der Anzahl günstiger Ergebnisse zur Gesamtzahl der Ergebnisse (Stichprobenraum) für ein Ereignis.
Einige der realen Beispiele für Wahrscheinlichkeit sind:
- Kartenspiele spielen, um die Wahrscheinlichkeit zu ermitteln, das Spiel zu gewinnen oder zu verlieren.
- Wettervorhersage, um den Regen vorherzusagen.
- Wahlergebnisse, um festzustellen, ob der Kandidat gewinnen oder verlieren wird.
- Prüfungsergebnisse, um festzustellen, ob der Kandidat bestehen oder nicht bestehen wird.
Wahrscheinlichkeitsformel
Wenn E ein Ereignis mit dem Stichprobenraum S ist und die Anzahl der günstigen Ergebnisse n(E) beträgt, dann ist die Wahrscheinlichkeit des Ereignisses E, d. h. P(E), gegeben durch:
P(E) = n(E) / n(S)
Was ist Kartenwahrscheinlichkeit?
Die Wahrscheinlichkeit, eine Karte oder eine Kartensammlung aus einem Stapel zu ziehen, wird Kartenwahrscheinlichkeit genannt. In einfachen Worten wird die Wahrscheinlichkeit im Zusammenhang mit Spielkarten als Kartenwahrscheinlichkeit bezeichnet. Da es sich um eine Art Wahrscheinlichkeit handelt, liegt sie immer zwischen 0 und 1. Wenn wir beispielsweise die Wahrscheinlichkeit ermitteln müssen, ein Ass aus dem Kartenspiel zu ziehen, also 4/52 = 1/13 [Da es 4 Asse gibt im Kartenspiel mit 52 Karten].
Kartenspiel in Wahrscheinlichkeit
Kartendecks sind eine Sammlung von 52 Karten, die es scheinbar schon seit Tausenden von Jahren gibt. Es wird davon ausgegangen, dass Kartenspiele oder Spielkarten entweder aus Indien oder China stammen. Der erste dokumentierte Beweis für diese Karten findet sich in 9ThJahrhundert in China während der Tang-Dynastie. Diese Karten ähnelten den heutigen Karten und waren ebenfalls in vier Farben unterteilt, aber der Name und das Symbol dieser Farben sind unterschiedlich, d. h. Münzen, Münzreihen, Myriaden und Myriaden von Zehnern.
Heutzutage gibt es diese Karten in verschiedenen Designs und sind in vier Farben unterteilt: Pik (♠), Kreuz (♣), Herz (❤) und Karo (◆). Für eine einzelne ausgewählte Karte beträgt der Stichprobenbereich 52, d. h. die Gesamtzahl der Ergebnisse für eine einzelne ausgewählte Karte aus einem Stapel beträgt 52.
n(S) für Kartenspiel = 52
Arten von Karten in einem Deck
Jedes Kartenspiel kann auf viele Arten klassifiziert werden. Einige der Parameter, nach denen Karten klassifiziert werden können, sind:
- Basierend auf Farben
- Basierend auf Anzügen
Lassen Sie uns diese Klassifizierung im Detail wie folgt verstehen:
Basierend auf Farben
Basierend auf den Farben kann ein Kartenspiel in zwei Kategorien eingeteilt werden:
- Rote Karten
- Schwarze Karten
Insgesamt 52 Karten sind zu gleichen Teilen in rote und schwarze Karten aufgeteilt, was bedeutet, dass der Stapel 26 rote und 26 schwarze Karten enthält.
Basierend auf Anzügen
Es gibt vier Farben im Kartenspiel:
- Herzen (❤)
- Diamanten (◆)
- Keulen (♣)
- Pik (♠)
Abgesehen von diesen gibt es noch eine weitere Klassifizierung von Karten, basierend auf dem Rang der Karten:
- As
- Zahlenkarten
- Bildkarten
As
Ass ist eine dieser Karten, die je nach Spiel entweder die wichtigste oder die unwichtigste ist. Auf dieser Karte steht A und jede Farbe hat eine dieser Karten, d. h. vier Ass-Karten.
Zahlenkarten
Von 2 bis 10 gibt es 9 Karten pro Farbe, also insgesamt 36 solcher Karten.
Bildkarten
Bildkarten enthalten, wie der Name schon sagt, eine Figur oder die Vorderseite der Figur auf der Karte. Es gibt drei Karten jeder Farbe, d. h. Bube, Dame, König. Somit gibt es insgesamt 12 Bildkarten.
Alle diese Klassifizierungen sind in der folgenden Tabelle aufgeführt.
| Kartenspiel (52 Karten) | ||||
|---|---|---|---|---|
| Farbige Karten | Schwarze Karten (26 Karten) | Rote Karten (26 Karten) | ||
| Anzüge | Spaten (13 Karten) | Club (13 Karten) | Herz (13 Karten) | Diamant (13 Karten) |
| Bildkarten (12 Karten in einem Stapel und 3 Karten in jeder Farbe) | K (König) | K (König) | K (König) | K (König) |
| Q (Königin) | Q (Königin) | Q (Königin) | Q (Königin) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Zahlenkarten (36 Karten in einem Deck und 9 Karten in einer Farbe) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Ass-Karten (4 Karten im Stapel und 1 Karte in einer Farbe) | A (Ass) | A (Ass) | A (Ass) | A (Ass) |
Kartenspiel-Diagramm
Die folgende Tabelle stellt die Klassifizierung des Spielkartenspiels dar:
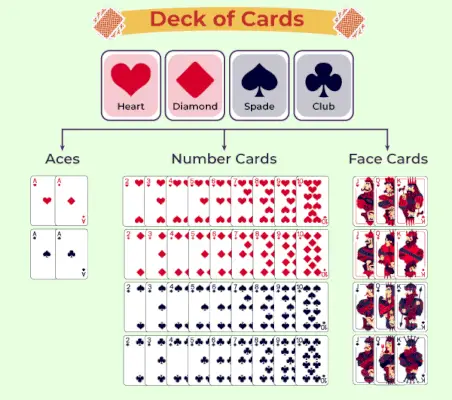
Spielkartenwahrscheinlichkeit
Einige der häufigsten Ereignisse bei Kartenwahrscheinlichkeiten werden in der folgenden Tabelle erläutert:
| Ereignis E zum Ziehen einer Karte | Wahrscheinlichkeit P(E) |
|---|---|
| Ein Ass | P(E) = 4 / 52 = 1 / 13 |
| Ein König | P(E) = 4 / 52 = 1 / 13 pvr vollständige Form |
| Eine Zahlenkarte | P(E) = 36 / 52 = 9 / 13 |
| Eine Bildkarte | P(E) = 12 / 52 = 3 / 13 |
| Eine Spatenkarte | P(E) = 13 / 52 = 1 / 4 |
| Eine Rote Karte | P(E) = 26 / 52 = 1 / 2 |
Wie ermittelt man die Wahrscheinlichkeit von Karten?
Die Schritte zum Ermitteln der Wahrscheinlichkeit von Ereignissen mit Karten sind die gleichen wie bei allen anderen Wahrscheinlichkeiten, die wie folgt angegeben werden:
Java-String-zu-Int-Konvertierung
Schritt 1: Ermitteln Sie zunächst die Anzahl der positiven Ergebnisse der gegebenen Frage.
Schritt 2: Ermitteln Sie dann die Gesamtzahl der Ergebnisse.
Schritt 3: Wenden Sie die Wahrscheinlichkeitsformel an, um die Kartenwahrscheinlichkeit zu ermitteln.
Beispiel: Wie groß ist die Wahrscheinlichkeit, ein Ass aus einem Kartenspiel zu ziehen?
Antwort:
Hier ist E das Ereignis, bei dem eine Ass-Karte gezogen wird
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen einer Ass-Karte aus dem Stapel = 4 (Es gibt 4 Ass-Karten in einem Stapel)
P(E) = n(E) / n(S) = 4 / 52
P(E) = 1 / 13
Wahrscheinlichkeit, eine Ass-Karte zu ziehen = 1 / 13
Beispielfragen zur Kartenwahrscheinlichkeit
Aufgabe 1: Wie groß ist die Wahrscheinlichkeit, die folgenden Karten aus einem Kartenspiel zu ziehen?
(i) ein Spaten
(ii) eine schwarze Karte
(iii) eine Zahlenkarte
Lösung:
(i) Hier ist E das Ereignis des Ziehens einer Pik-Karte
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen einer Pik-Karte vom Stapel = 13 (Es gibt 13 Karten jeder Farbe in einem Stapel)
P(E) = n(E) / n(S) = 13 / 52
P(E) = 1 / 4
Wahrscheinlichkeit, einen Spaten zu ziehen = 1 / 4
(ii) Hier ist E das Ereignis des Ziehens einer schwarzen Karte
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen einer schwarzen Karte vom Stapel = 26 (Es gibt 26 schwarze Karten in einem Stapel)
P(E) = n(E) / n(S) = 26 / 52
P(E) = 1 / 2
Wahrscheinlichkeit, eine schwarze Karte zu ziehen = 1 / 2
(iii) Hier ist E das Ereignis des Ziehens einer Zahlenkarte
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen einer Zahlenkarte vom Stapel = 36 (Es gibt 36 Zahlenkarten in einem Stapel)
P(E) = n(E) / n(S) = 36 / 52
P(E) = 9 / 13
Wahrscheinlichkeit, eine Zahlenkarte zu ziehen = 9 / 13
Aufgabe 2: Wie groß ist die Wahrscheinlichkeit, die folgenden Karten aus einem Kartenspiel zu ziehen?
(i) Ein König oder eine schwarze Karte
(ii) Eine rote und eine Ass-Karte
Lösung:
(i) Hier ist E das Ereignis, bei dem ein König oder eine schwarze Karte gezogen wird
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen eines Königs oder einer schwarzen Karte aus dem Deck = 26 + 2 = 28 (Es gibt 26 schwarze Karten, von denen 2 Könige sind und die restlichen 2 Könige von Schwarz in einem Deck)
P(E) = n(E) / n(S) = 28 / 52
P(E) = 7 / 13
Wahrscheinlichkeit, einen König oder eine schwarze Karte zu ziehen = 7 / 13
(ii) Hier ist E das Ereignis des Ziehens einer roten und einer Ass-Karte
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Zeichenfolge vergleichen mitAnzahl der günstigen Ergebnisse = n(E) = Ziehen einer roten und einer Ass-Karte vom Stapel = 2 (Es gibt 26 rote Karten, von denen 2 Ass-Karten sind)
Gemäß der Frage sollte die gezogene Karte sowohl Rot als auch Ass sein. Daher ist n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1 / 26
Wahrscheinlichkeit, eine rote und eine Ass-Karte zu ziehen = 1 / 26
Aufgabe 3: Wie groß ist die Wahrscheinlichkeit, die folgenden Karten aus einem Kartenspiel zu ziehen?
(i) Eine Nicht-Club-Karte
(ii) Eine Karte ohne Bild
Lösung:
(i) Hier ist E das Ereignis des Ziehens einer Nicht-Clubkarte
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen einer Nicht-Club-Karte vom Kartenstapel = 39 (Es gibt 13 Kreuze in einem Kartenstapel, Nicht-Kartenstapel = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39 / 52
P(E) = 3 / 4
Wahrscheinlichkeit, eine Nicht-Vereinskarte zu ziehen = 3 / 4
(ii) Hier ist E das Ereignis des Ziehens einer Nicht-Bildkarte
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen einer Nicht-Bildkarte aus dem Stapel = 40 (Es gibt 12 Bildkarten in einem Stapel, Nicht-Deck = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40 / 52
P(E) = 10 / 13
Wahrscheinlichkeit, eine Nicht-Vereinskarte zu ziehen = 10 / 13
Aufgabe 4: Wie groß ist die Wahrscheinlichkeit, eine Karte zu ziehen, die weder rot noch eine Bildkarte ist?
Lösung:
Hier ist E das Ereignis, bei dem weder eine rote noch eine Bildkarte gezogen wird
Gesamtzahl der Ergebnisse in einem Deck n(S) = 52
Anzahl der günstigen Ergebnisse = n(E) = Ziehen weder einer roten noch einer Bildkarte vom Stapel.
Gesamtzahl der roten Karten = 26
Es gibt insgesamt 12 Bildkarten in einem Stapel, aber 6 rote Bildkarten wurden bereits entfernt. Also verbleibende Bildkarten = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/ 52
P(E) = 8 / 13
Wahrscheinlichkeit, weder eine rote noch eine Bildkarte zu ziehen = 8 / 13
Aufgabe 5: Wie groß ist die Wahrscheinlichkeit, zwei Karten aus einem Kartenspiel mit Ersetzung zu ziehen, wenn die erste Karte ein Herz und die zweite Karte eine Karo ist?
Lösung:
Wahrscheinlichkeit, die erste Karte als Herz zu ziehen = 13 / 52
Nach dem Ziehen der ersten Karte wird die Karte entfernt.
Wahrscheinlichkeit, die zweite Karte als Karo zu ziehen = 13 / 51
Wahrscheinlichkeit, die erste Karte als Herz und die zweite als Karo zu ziehen = (13 / 52) × (13 / 51)
Numpy-LinspaceWahrscheinlichkeit, die erste Karte als Herz und die zweite als Karo zu ziehen = 13 / 204
FAQs zur Kartenwahrscheinlichkeit
1. Was ist die Kartenwahrscheinlichkeit?
Die Wahrscheinlichkeit, eine Karte aus dem Kartenspiel zu ziehen, wird als Kartenwahrscheinlichkeit bezeichnet.
2. Listen Sie die Arten von Farben in einem Kartenspiel auf.
Es gibt vier Arten von Farben in einem Kartenspiel. Sie sind:
- Herzen
- Diamanten
- Spaten
- Vereine
3. Wie groß ist der Probenplatz für das Kartendeck, wenn eine Karte aus dem Deck gezogen wird?
Der Beispielbereich für ein Kartenspiel, wenn eine Karte gezogen wird, enthält 52 Ergebnisse.
4. Schreiben Sie die Formel zum Ermitteln der Wahrscheinlichkeit.
Die Formel zur Ermittlung der Wahrscheinlichkeit lautet:
Wahrscheinlichkeit eines Ereignisses = Anzahl günstiger Ereignisse / Gesamtzahl der Ergebnisse
ODER
P(E) = n(E) / n(S)
5. Wie viele Bildkarten enthält ein Kartenspiel?
In einem Kartenspiel sind 12 Bildkarten vorhanden.
