Wir kennen ein Baum ist eine nichtlineare Datenstruktur. Die Anzahl der Kinder ist nicht begrenzt. AWas ist ein vollständiger Binärbaum?
Ein vollständiger Binärbaum ist eine spezielle Art von Binärbaum, bei dem alle Ebenen des Baums vollständig gefüllt sind, mit Ausnahme der Knoten der untersten Ebene, die so weit wie möglich von links gefüllt werden.

Kompletter Binärbaum
Einige Terminologie des vollständigen Binärbaums:
- Wurzel – Knoten, bei dem keine Kante vom übergeordneten Knoten kommt. Beispiel: Knoten A
- Kind – Knoten mit einer eingehenden Kante werden als Kind bezeichnet. Beispiel – Die Knoten B, F sind die untergeordneten Knoten von A bzw. C.
- Geschwister – Knoten mit demselben übergeordneten Knoten sind Geschwister. Beispiel: D und E sind Geschwister, da sie denselben Elternteil B haben.
- Grad eines Knotens – Anzahl der Kinder eines bestimmten Elternteils. Beispiel: Grad von A ist 2 und Grad von C ist 1. Grad von D ist 0.
- Interne/externe Knoten – Blattknoten sind externe Knoten und Nicht-Blattknoten sind interne Knoten.
- Ebene – Zählen Sie Knoten in einem Pfad, um einen Zielknoten zu erreichen. Beispiel: Die Ebene von Knoten D ist 2, da die Knoten A und B den Pfad bilden.
- Höhe – Anzahl der Kanten, um den Zielknoten zu erreichen. Die Wurzel liegt auf der Höhe 0. Beispiel – Die Höhe des Knotens E beträgt 2, da er zwei Kanten von der Wurzel entfernt hat.
Eigenschaften des vollständigen Binärbaums:
- Ein vollständiger Binärbaum ist ein echter Binärbaum, bei dem alle Blätter die gleiche Tiefe haben.
- In einem vollständigen Binärbaum gibt es eine Anzahl von Knoten in der Tiefe D Ist 2 D .
- In einem vollständigen Binärbaum mit N Knotenhöhe des Baumes ist log(n+1) .
- Alle Ebenen außer der letzten Ebene sind komplett voll.
Perfekter Binärbaum vs Vollständiger Binärbaum:
Ein binärer Baum der Höhe „h“ mit der maximalen Anzahl an Knoten ist a perfekt Binärbaum.
Für eine bestimmte Höhe H , die maximale Anzahl von Knoten beträgt 2 h+1 -1 .
A vollständig Binärbaum der Höhe h ist bis zur Höhe ein perfekter Binärbaum h-1 und im letzten Ebenenelement werden in der Reihenfolge von links nach rechts gespeichert.
Beispiel 1:
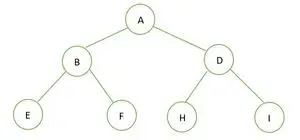
Ein Binärbaum
Die Höhe des angegebenen Binärbaums beträgt 2 und die maximale Anzahl von Knoten in diesem Baum beträgt n=2h+1-1 = 22+1-1 = 23-1 = 7 .
Daraus können wir schließen, dass dies der Fall ist ein perfekter Binärbaum .
Nun zu einem vollständigen Binärbaum. Er ist bis zur Höhe voll h-1 d.h.; 1, und die Elemente der letzten Ebene werden in der Reihenfolge von links nach rechts gespeichert. Daher handelt es sich auch um einen vollständigen Binärbaum. Hier ist die Darstellung von Elementen, wenn sie in einem Array gespeichert sind

Element, das Ebene für Ebene in einem Array gespeichert wird
Im Array werden alle Elemente fortlaufend gespeichert.
Beispiel 2:
iterierende Karte Java
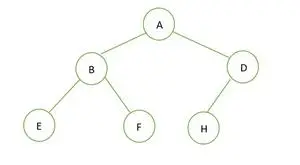
Ein binärer Baum
Die Höhe des angegebenen Binärbaums beträgt 2 und die maximale Anzahl der Knoten, die dort vorhanden sein sollten, beträgt 2h+1– 1 = 22+1– 1 = 23– 1 = 7 .
Aber die Anzahl der Knoten im Baum ist 6 . Daher ist es so kein perfekter Binärbaum .
Nun zu einem vollständigen Binärbaum. Er ist bis zur Höhe voll h-1 d.h.; 1 und das letzte Ebenenelement werden in der Reihenfolge von links nach rechts gespeichert. Daher ist dies ein vollständiger Binärbaum . Speichern Sie das Element in einem Array und es sieht so aus:
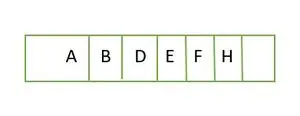
Element, das Ebene für Ebene in einem Array gespeichert wird
Beispiel 3:
Datum in String konvertieren
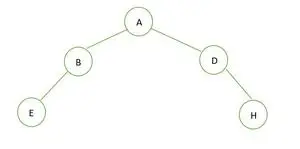
Ein binärer Baum
Die Höhe des Binärbaums beträgt 2 und die maximale Anzahl der Knoten, die dort vorhanden sein können, beträgt 7, es gibt jedoch nur 5 Knoten, daher ist dies der Fall kein perfekter Binärbaum .
Im Falle eines vollständigen Binärbaums sehen wir, dass die Elemente auf der letzten Ebene nicht von links nach rechts gefüllt werden. So ist es kein vollständiger Binärbaum .
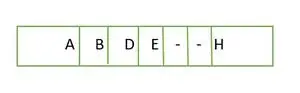
Element, das Ebene für Ebene in einem Array gespeichert wird
Die Elemente im Array sind nicht fortlaufend.
Vollständiger Binärbaum vs. vollständiger Binärbaum:
Bei einem vollständigen Binärbaum hat jeder Knoten entweder 2 oder 0 Kinder.
Beispiel 1:
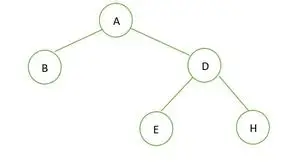
Ein binärer Baum
In dem gegebenen Binärbaum gibt es keinen Knoten mit Grad 1, also entweder 2 oder 0 Kinder für jeden Knoten, also ist es so ein vollständiger Binärbaum .
Für einen vollständigen Binärbaum werden Elemente Ebene für Ebene und nicht von der äußersten linken Seite in der letzten Ebene gespeichert. Daher ist das so kein vollständiger Binärbaum . Die Array-Darstellung lautet:
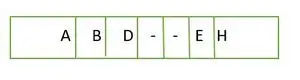
Element, das Ebene für Ebene in einem Array gespeichert wird
Beispiel 2:
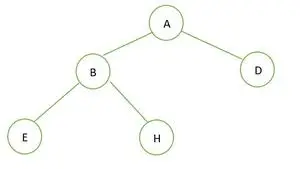
Ein binärer Baum
Im angegebenen Binärbaum gibt es keinen Knoten mit dem Grad 1. Jeder Knoten hat den Grad 2 oder 0. Daher ist er a vollständiger Binärbaum .
Für einen vollständigen Binärbaum werden Elemente Ebene für Ebene gespeichert und von der äußersten linken Seite der letzten Ebene aus gefüllt. Daher dieses a vollständiger Binärbaum . Unten ist die Array-Darstellung des Baums:
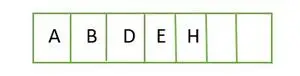
Element, das Ebene für Ebene in einem Array gespeichert wird
Beispiel 3:
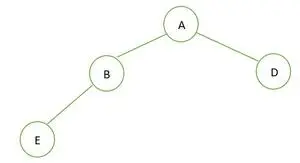
Ein binärer Baum
In dem gegebenen Binärbaum hat Knoten B den Grad 1, was die Eigenschaft eines vollständigen Binärbaums verletzt, also ist er es kein vollständiger Binärbaum
Minimax-Algorithmus
Für einen vollständigen Binärbaum werden Elemente Ebene für Ebene gespeichert und von der äußersten linken Seite der letzten Ebene aus gefüllt. Daher ist dies ein vollständiger Binärbaum . Die Array-Darstellung des Binärbaums lautet:
Java-Programmschleife
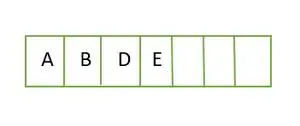
Element, das Ebene für Ebene in einem Array gespeichert wird
Beispiel 4:
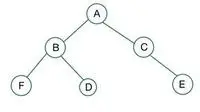
ein binärer Baum
In dem gegebenen Binärbaum hat Knoten C den Grad 1, was die Eigenschaft eines vollständigen Binärbaums verletzt, also ist er es kein vollständiger Binärbaum
Für einen vollständigen Binärbaum werden Elemente Ebene für Ebene gespeichert und von der äußersten linken Seite der letzten Ebene aus gefüllt. Hier verstößt Knoten E gegen die Bedingung. Daher ist das so kein vollständiger Binärbaum .
Erstellung eines vollständigen Binärbaums:
Wir kennen ein vollständiger Binärbaum ist ein Baum, in dem bis auf die letzte Ebene (z. B l )Alle anderen Ebenen haben ( 2l ) Knoten und die Knoten sind von links nach rechts aufgereiht.
Es kann mithilfe eines Arrays dargestellt werden. Wenn das übergeordnete Element der Index ist ich also ist das linke Kind bei 2i+1 und das richtige Kind ist dabei 2i+2 .
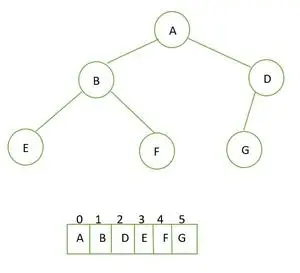
Vollständiger Binärbaum und seine Array-Darstellung
Algorithmus:
Für die Erstellung eines Kompletter Binärbaum , wir benötigen a Schritt 1: Initialisieren Sie die Wurzel mit einem neuen Knoten, wenn der Baum leer ist.
Schritt 2: Wenn der Baum nicht leer ist, holen Sie sich das vordere Element
- Wenn das vordere Element kein linkes untergeordnetes Element hat, setzen Sie das linke untergeordnete Element auf einen neuen Knoten
- Wenn das richtige Kind nicht vorhanden ist, legen Sie das richtige Kind als neuen Knoten fest
Schritt 3: Wenn der Knoten beide Kinder hat, dann Pop es aus der Warteschlange.
str.replace in Java
Schritt 4: Stellen Sie die neuen Daten in die Warteschlange.
Illustration:
Betrachten Sie das folgende Array:
1. Das 1. Element ist die Wurzel (Wert am Index = 0 )
A wird als Wurzel genommen
2. Das nächste Element (bei Index = 1 ) bleibt übrig und das dritte Element (Index = 2 ) wird das rechte Kind von root sein
B als linkes Kind und D als rechtes Kind
3. Vierter (Index = 3 ) und fünftes Element (Index = 4 ) wird das linke und rechte Kind des B-Knotens sein
E und F sind linke und rechte Kinder von B
4. Nächstes Element (Index = 5 ) wird das linke Kind des Knotens D sein
G wird zum linken Kind des D-Knotens gemacht
Auf diese Weise entsteht ein vollständiger Binärbaum.
Implementierung: Für die Implementierung des Aufbaus eines vollständigen Binärbaums aus der Durchquerung der Ebenenreihenfolge wird in angegeben dieser Beitrag .
Anwendung des vollständigen Binärbaums:
- Heap-Sortierung
- Heap-sortierte Datenstruktur
Überprüfen Sie, ob ein bestimmter Binärbaum vollständig ist oder nicht: Folgen dieser Beitrag um zu überprüfen, ob der angegebene Binärbaum vollständig ist oder nicht.




