Komplexe Zahlen sind die natürliche Fortsetzung reeller Zahlen. In der modernen Zeit werden komplexe Zahlen in vielen Bereichen wie der digitalen Signalverarbeitung, der Kryptographie und vielen computerbezogenen Bereichen verwendet.

In diesem Artikel lernen wir etwas über imaginäre Zahlen, komplexe Zahlen und deren Typ, verschiedene Operationen mit komplexen Zahlen, Eigenschaften komplexer Zahlen, Anwendung komplexer Zahlen usw.

Definition komplexer Zahlen

Komplexe Zahlen sind die Zahlen des Formulars (a + i b) Wo A & B sind die reellen Zahlen und ich ist eine imaginäre Einheit namens Iota, die √-1 darstellt. Beispielsweise ist 2 + 3i eine komplexe Zahl, bei der 2 eine reelle Zahl und 3i eine imaginäre Zahl ist. Komplexe Zahlen können als a + ib geschrieben werden, wobei a und b rationale Zahlen sind, die auf einer Zahlengerade dargestellt werden können, die bis verläuft Unendlichkeit .

Modul der komplexen Zahl

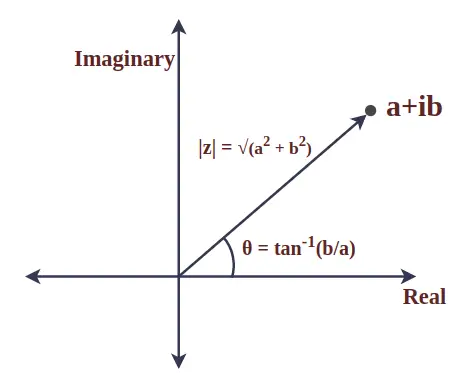
Der Modul der komplexen Zahl ist der Absolutwert und stellt den Abstand zwischen dem Ursprung und dem gegebenen Punkt dar. Sie wird auch als Betrag der komplexen Zahl bezeichnet. Betrachten wir eine komplexe Zahl z = a + ib, dann ist der Modul von z definiert als:

string.replaceall Java

|z| = √(a ² + b ² )

Wo,

• A ist der Realteil der komplexen Zahl z, und
• B ist der Imaginärteil der komplexen Zahl z.

Argument der komplexen Zahl

Der Winkel zwischen dem Radiusvektor einer komplexen Zahl und der positiven x-Achse wird als Argument einer komplexen Zahl bezeichnet. Für eine komplexe Zahl z = a + ib ist sie mathematisch gegeben durch:

θ = tan ^-1 (b/a)

Wo,

• A ist der Realteil der komplexen Zahl z, und
• B ist der Imaginärteil der komplexen Zahl z.

Potenz von i(iota)

Das i(iota) ist definiert als die Quadratwurzel von -1. Somit kann jede Potenz von i als wiederholte Multiplikation von i mit sich selbst ausgedrückt werden, d. h.

• i = √(-1)
• ich²= -1
• ich³= – ich
• ich⁴= 1
• ich⁵= ich
• ich⁶= – 1
• und so weiter..

Bedarf an komplexen Zahlen

In der Antike kannten die Menschen nur solche natürlichen Zahlen Zahlen sind von Natur aus am intuitivsten, da das menschliche Gehirn sie bereits anhand visueller Darstellungen von Dingen wie Schafen und Essen versteht. Somit haben wir nur die Menge der natürlichen Zahlen ( N ), aber in natürlichen Zahlen gibt es keine Lösung für die Gleichung x + a = b (a> b) und a, b ∈ N. Somit entstand eine Erweiterung natürlicher Zahlen, d. h. ganze Zahlen( ICH ).

Auch in dieser Zahlenmenge gibt es keine Lösung für die Gleichung ax = b (a ≠ 0) und a, b ∈ I, wobei a und b beide ganze Zahlen sind. Somit wird eine Menge ganzer Zahlen (I) zu einer Menge rationaler Zahlen ( Q ).

Auch in dieser Menge rationaler Zahlen gibt es keine Lösung für die Gleichung x²= a (a> 0) und a ∈ Q. Somit ist Q wird um Zahlen mit x erweitert²= a(für a> 0), also irrationale Zahlen. Diese Menge heißt Reelle Zahlen und wird dargestellt durch R .

Nun wurde lange Zeit angenommen, dass wir diese Menge reeller Zahlen nicht erweitern müssen, um eine weitere größere Menge zu bilden, da diese Zahlensammlung vollständig zu sein scheint. Aber auch hier entsteht bei dieser Zahlenmenge ein neues Problem, nämlich dass es keine reelle Zahl mit x gibt²= a (a <0) und a ∈ R. Somit wird die Menge der reellen Zahlen weiter erweitert, um alle derart bewerteten und benannten komplexen Zahlen dieser Menge einzuschließen, und wird durch dargestellt C .

Klassifikation komplexer Zahlen

Wie wir wissen, ist die Standardform einer komplexen Zahl z = (a + i b) wobei a, b ∈ R und i iota (eine imaginäre Einheit) ist. Abhängig von den Werten von a (Realteil genannt) und b (Imaginärteil genannt) werden die komplexen Zahlen in vier Typen eingeteilt:

• Komplexe Zahl Null
• Rein reelle Zahlen
• Rein imaginäre Zahlen
• Imaginäre Zahlen

Lassen Sie uns diese Typen im Detail kennenlernen.

Komplexe Zahl Null

Für jede komplexe Zahl z = a + ib, wenn a = 0 und b = 0, dann wird die komplexe Zahl als komplexe Zahl Null bezeichnet. Das einzige Beispiel hierfür ist beispielsweise 0.

Rein reelle Zahlen

Für jede komplexe Zahl z = a + ib, wenn a ≠ 0 & b = 0, dann wird die komplexe Zahl eine rein reelle Zahl genannt, d. h. eine Zahl ohne Imaginärteil. Alle reellen Zahlen sind Beispiele dafür, wie zum Beispiel 2, 3, 5, 7 usw.

Rein imaginäre Zahlen

Für jede komplexe Zahl z = a + ib, wenn a = 0 & b ≠ 0, dann wird eine komplexe Zahl eine rein imaginäre Zahl genannt, d. h. eine Zahl ohne Realteil. Alle Zahlen ohne Realteile sind Beispiele für diesen Zahlentyp, d. h. -7i, -5i, -i, i, 5i, 7i usw.

Imaginäre Zahlen

Für jede komplexe Zahl z = a + ib, wenn a ≠ 0 & b ≠ 0, dann heißt eine komplexe Zahl an imaginäre Zahl . Zum Beispiel (-1 – i), (1 + i), (1 – i), (2 + 3i) usw.

Verschiedene Formen komplexer Zahlen

Es gibt verschiedene Formen komplexer Zahlen:

• Rechteckige Form
• Polarform
• Exponentielle Form

Lassen Sie uns nun im Detail mehr über sie erfahren.

Rechteckige Form

Rechteckige Form Ist auch genannt Standardform und es wird vertreten durch (a + ib), wobei a und b die reellen Zahlen sind.

Zum Beispiel: (5 + 5i), (-7i), (-3 – 4i) usw.

Polarform

Polarform ist die Darstellung einer komplexen Zahl mit Polarkoordinaten [wobei Koordinaten als (r, θ) dargestellt werden, wobei r der Abstand vom Ursprung und θ der Winkel zwischen der Verbindungslinie zwischen Punkt und Ursprung und der positiven x-Achse ist) werden zur Darstellung einer komplexen Zahl verwendet. Jede komplexe Zahl wird dargestellt als r [cos θ + i sin θ].

Zum Beispiel: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] usw.

Exponentielle Form

Exponentialformen komplexer Zahlen ist die Darstellung komplexer Zahlen unter Verwendung der Eulerschen Formel und in dieser Form wird die komplexe Zahl durch re dargestellt^ich, wobei r der Abstand eines Punktes vom Ursprung und θ der Winkel zwischen der positiven x-Achse und dem Radiusvektor ist.

Zum Beispiel: z^ich(0), Es ist^i(π/2), 5.e^i(π/6), usw.

Bash for-Schleife

Notiz: Alle drei oben diskutierten Formen der komplexen Zahlen sind ineinander umwandelbar, d. h. sie können sehr einfach von einer Form in eine andere umgewandelt werden.

Operationen mit komplexen Zahlen

Die folgenden Operationen können für komplexe Zahlen ausgeführt werden:

• Zusatz
• Subtraktion
• Multiplikation
• Aufteilung
• Konjugation

Addition komplexer Zahlen

Wir können zwei komplexe Zahlen addieren, indem wir einfach ihren Real- und Imaginärteil getrennt addieren.

Beispiel: (3 + 2i) + (1 + 4i) = 4 + 6i.

Subtraktion komplexer Zahlen

Wir können zwei komplexe Zahlen subtrahieren, indem wir einfach ihren Real- und Imaginärteil getrennt voneinander subtrahieren.

Beispiel: (3 + 2i) – (1 + 4i) = 2 – 2i.

Multiplikation komplexer Zahlen

Wir können zwei komplexe Zahlen mithilfe der Verteilungseigenschaft und der Tatsache multiplizieren, dass i²= -1.

Beispiel: (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Division komplexer Zahlen

Wir können eine komplexe Zahl durch eine andere dividieren, indem wir einfach sowohl den Zähler als auch den Nenner mit dem konjugierten Komplex des Nenners multiplizieren und den Ausdruck weiter vereinfachen.

Zum Beispiel: (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Konjugation komplexer Zahlen

Wir können das leicht finden Konjugat einer komplexen Zahl, indem man einfach das Vorzeichen seines Imaginärteils ändert. Das Konjugat einer komplexen Zahl wird oft mit einem Balken über der Zahl gekennzeichnet, z. B. z̄.

Das Konjugat von 3 + 2i ist beispielsweise 3 – 2i.

Identitäten für komplexe Zahlen

Für zwei beliebige komplexe Zahlen z₁und z₂Folgende algebraische Identitäten können angegeben werden:

• (Mit ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 Z ₁ × z ₂
• (Mit ₁ - Mit ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (Mit ₁ ) ² - (Mit ₂ ) ² = (z ₁ + z ₂ )(Mit ₁ - Mit ₂ )
• (Mit ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² Mit ₂ +3(z ₂ ) ² Mit ₁ + (z ₂ ) ³
• (Mit ₁ - Mit ₂ ) ³ = (z ₁ ) ³ – 3(z ₁ ) ² Mit ₂ +3(z ₂ ) ² Mit ₁ - (Mit ₂ ) ³

Formeln im Zusammenhang mit komplexen Zahlen

Es gibt einige Formeln für komplexe Zahlen, von denen einige wie folgt lauten:

Eulers Formel

Eulers Formel zeigt die Beziehung zwischen der imaginären Potenz des Exponenten und dem trigonometrischen Verhältnis sin und cos und ist gegeben durch:

Es ist ^ix = cos x + i sin x

De Moivres Formel

De Moivres Formel drückt das n aus^ThPotenz einer komplexen Zahl in Polarform und ist gegeben durch:

(cos x + i sin x) ^N = cos(nx) + i sin(nx)

Komplexe Ebene

Die Ebene, auf der die komplexen Zahlen eindeutig dargestellt werden, wird Komplexe Ebene oder Argand-Ebene oder Gaußsche Ebene genannt.

Die komplexe Ebene hat zwei Achsen:

• X-Achse oder reale Achse
• Y-Achse oder imaginäre Achse

X-Achse oder reale Achse

• Alle rein reellen komplexen Zahlen werden eindeutig durch einen Punkt darauf dargestellt.
• Dazu wird der Realteil Re(z) aller komplexen Zahlen aufgetragen.
• Deshalb wird auch X-Achse genannt Echte Achse .

Y-Achse oder imaginäre Achse

• Alle rein imaginären komplexen Zahlen werden durch einen Punkt auf ihr eindeutig dargestellt.
• Dazu wird der Imaginärteil Im(z) aller komplexen Zahlen aufgetragen.
• Deshalb wird auch Y-Achse genannt Imaginäre Achse .

entspricht einer Zeichenfolge in Java

Geometrische Darstellung komplexer Zahlen

Wie wir wissen, wird jede komplexe Zahl (z = a + i b) durch einen eindeutigen Punkt p(a, b) auf der komplexen Ebene dargestellt und jeder Punkt auf der komplexen Ebene stellt eine eindeutige komplexe Zahl dar.

Um eine beliebige komplexe Zahl z = (a + i b) auf der komplexen Ebene darzustellen, befolgen Sie diese Konventionen:

• Der Realteil von z (Re(z) = a) wird zur X-Koordinate des Punktes p

• Der Imaginärteil von z (Im(z) = b) wird zur Y-Koordinate des Punktes p

Und schließlich z (a + i b) ⇒ p (a, b), was ein Punkt auf der komplexen Ebene ist.

Eigenschaften komplexer Zahlen

Es gibt verschiedene Eigenschaften komplexer Zahlen, von denen einige wie folgt lauten:

• Für jede komplexe Zahl z = a + ib gilt, wenn z = 0, dann a = 0 sowie b = 0.
• Für 4 reelle Zahlen a, b, c und d mit z₁= a + ib und z₂= c + id. Wenn z₁= z₂dann ist a = c und b = d.
• Die Addition einer komplexen Zahl mit ihrer Konjugierten ergibt eine rein reelle Zahl, d. h. z + z̄ = reelle Zahl.

Sei z = a + ib,

z + z̄ = a + eins + a – eins

⇒ z + z̄ = 2a (was rein real ist)

• Das Produkt einer komplexen Zahl mit ihren konjugierten Ergebnissen ist ebenfalls eine rein reelle Zahl, d. h. z × z̄ = reelle Zahl

Dann sei z = a + ib

z × z̄ = (a + eins) × (a – eins)

⇒ z × z̄= a²- ich²B²

⇒ z × z̄ = a²+ b²(was rein real ist)

• Komplexe Zahlen sind kommutativ unter der Operation der Addition und Multiplikation. Betrachten wir zwei komplexe Zahlen z₁und z₂, und dann

Mit ₁ +z ₂ = z ₂ +z ₁

Mit ₁ × z ₂ = z ₂ × z ₁

• Komplexe Zahlen sind assoziativ mit der Operation der Addition und Multiplikation. Betrachten wir drei komplexe Zahlen z₁, Mit₂, und z₃Dann

(Mit ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Mit ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Komplexe Zahlen halten die Verteilungseigenschaft auch die Multiplikation über die Addition. Betrachten wir drei komplexe Zahlen z₁, Mit₂, und z₃Dann

Mit ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Mehr lesen,

• Komplexe Zahlen dividieren
• Z-Balken in komplexen Zahlen

Beispiele zu komplexen Zahlen

Beispiel 1: Zeichnen Sie diese komplexen Zahlen z = 3 + 2i auf der komplexen Ebene.

Linux-Änderungsdatei

Lösung:

Gegeben:

Mit = 3 + 2 ich

Der Punkt ist also z(3, 2). Jetzt zeichnen wir diesen Punkt in der folgenden Grafik ein. Hier in dieser Grafik stellt die x-Achse den Realteil und die y-Achse den Imaginärteil dar.

Beispiel 2: Zeichnen Sie diese komplexen Zahlen z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) auf der komplexen Ebene.

Lösung:

Tupel Java

Gegeben:

Mit₁= (2 + 2 i)

Mit₂= (-2 + 3 i)

Mit₃= (-1 – 3 i)

Mit₄= (1 – i)

Die Punkte sind also z₁(2, 2), z₂(-2, 3), z₃(-1, -3) und z₄(1, -1). Nun zeichnen wir diese Punkte in der folgenden Grafik ein. Hier in dieser Grafik stellt die X-Achse den Realteil und die Y-Achse den Imaginärteil dar.

FAQs zu komplexen Zahlen

Komplexe Zahlen definieren.

Zahlen der Form a+ib werden komplexe Zahlen genannt, wobei a und b die reellen Zahlen sind und i die imaginäre Einheit ist, die die Quadratwurzel von -1 darstellt.

Was ist der Unterschied zwischen einer reellen Zahl und einer komplexen Zahl?

Der Unterschied zwischen reellen und komplexen Zahlen besteht darin, dass wir nur eine Zahl benötigen, um jede reelle Zahl darzustellen, aber zwei reelle Zahlen, um jede komplexe Zahl darzustellen.

Was ist der Realteil und der Imaginärteil einer komplexen Zahl?

In einer komplexen Zahl a + ib ist a der Realteil der komplexen Zahl und b heißt der Imaginärteil der komplexen Zahl.

Was ist das komplexe Konjugat einer komplexen Zahl?

Für eine komplexe Zahl a + ib wird a – ib als ihr komplexes Konjugat bezeichnet. Komplexe Konjugate können durch einfaches Ändern des Vorzeichens des Imaginärteils gefunden werden.

Was ist der Modul einer komplexen Zahl?

Der Abstand zwischen dem Ursprung und dem Punkt, der durch eine komplexe Zahl in der Argandebene dargestellt wird, wird als Modul dieser vollständigen Zahl bezeichnet und ist für z = a + ib mathematisch gegeben durch:

|z| = √(a ² + b ² )

Was ist das Argument einer komplexen Zahl?

Der Winkel zwischen dem Radiusvektor einer komplexen Zahl und der positiven x-Achse wird als Argument einer komplexen Zahl bezeichnet und ist für z = a + ib mathematisch gegeben durch:

θ = tan ^-1 (b/a)

Was ist die Polarform einer komplexen Zahl?

Für jede komplexe Zahl, z = a + ib, ist die Polarform gegeben durch:

r [cos θ + i sin θ]

Wie lautet Eulers Formel?

Eulers Formel zeigt die Beziehung zwischen der imaginären Potenz des Exponenten und dem trigonometrischen Verhältnis sin und cos und ist gegeben durch:

Es ist ^ix = cos x + i sin x