Die Löschfunktion wird verwendet, um den angegebenen Knoten aus einem binären Suchbaum zu löschen. Allerdings müssen wir einen Knoten so aus einem binären Suchbaum löschen, dass die Eigenschaft des binären Suchbaums nicht verletzt wird. Es gibt drei Situationen zum Löschen eines Knotens aus dem binären Suchbaum.
Der zu löschende Knoten ist ein Blattknoten
Dies ist der einfachste Fall. In diesem Fall ersetzen Sie den Blattknoten durch NULL und geben einfach den zugewiesenen Speicherplatz frei.
Im folgenden Bild löschen wir den Knoten 85, da es sich bei dem Knoten um einen Blattknoten handelt. Daher wird der Knoten durch NULL ersetzt und zugewiesener Speicherplatz wird freigegeben.
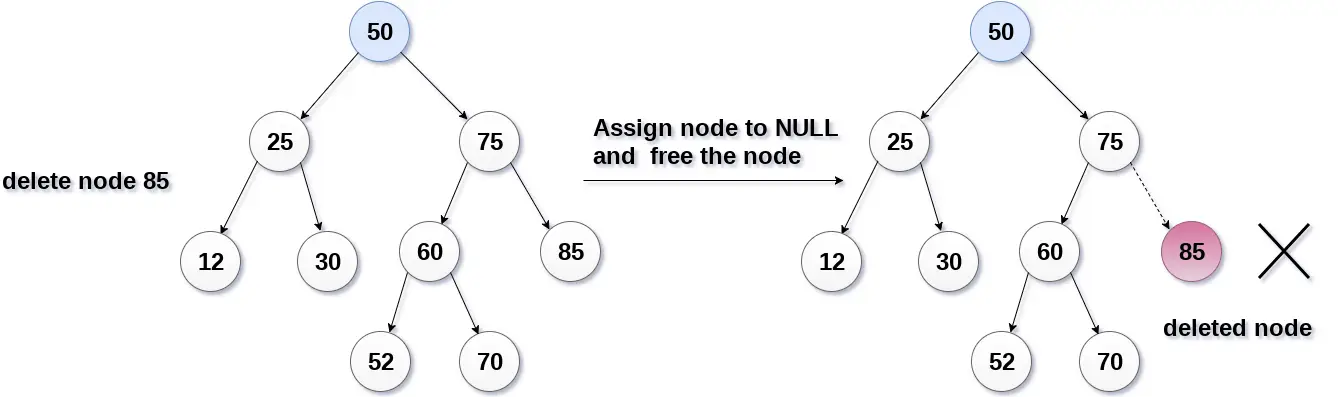
Der zu löschende Knoten hat nur ein Kind.
Ersetzen Sie in diesem Fall den Knoten durch seinen untergeordneten Knoten und löschen Sie den untergeordneten Knoten, der nun den zu löschenden Wert enthält. Ersetzen Sie es einfach durch NULL und geben Sie den zugewiesenen Speicherplatz frei.
Im folgenden Bild soll der Knoten 12 gelöscht werden. Es hat nur ein Kind. Der Knoten wird durch seinen untergeordneten Knoten ersetzt und der ersetzte Knoten 12 (der jetzt der Blattknoten ist) wird einfach gelöscht.

Der zu löschende Knoten hat zwei Kinder.
Im Vergleich zu den beiden anderen Fällen handelt es sich um einen etwas komplexen Fall. Der Knoten, der gelöscht werden soll, wird jedoch rekursiv durch seinen Nachfolger oder Vorgänger in der Reihenfolge ersetzt, bis der Knotenwert (der gelöscht werden soll) auf dem Blatt des Baums platziert wird. Ersetzen Sie nach dem Vorgang den Knoten durch NULL und geben Sie den zugewiesenen Speicherplatz frei.
Arrayliste in Java
Im folgenden Bild soll der Knoten 50 gelöscht werden, der der Wurzelknoten des Baums ist. Die geordnete Durchquerung des unten angegebenen Baums.
6, 25, 30, 50, 52, 60, 70, 75.
Ersetzen Sie 50 durch seinen geordneten Nachfolger 52. Jetzt wird 50 auf das Blatt des Baums verschoben, das einfach gelöscht wird.

Algorithmus
Löschen (BAUM, ITEM)
Schreiben Sie „Element nicht im Baum gefunden“, ELSE IF ITEM DATA
Löschen(BAUM->LINKS, ITEM)
ELSE IF ITEM > TREE -> DATA
Löschen(BAUM -> RECHTS, ITEM)
ELSE IF BAUM -> LINKS UND BAUM -> RECHTS
SET TEMP = findLargestNode(TREE -> LEFT)
BAUM SETZEN -> DATEN = TEMP -> DATEN
Löschen (BAUM -> LINKS, TEMP -> DATEN)
ANDERS
SET TEMP = BAUM
WENN BAUM -> LINKS = NULL UND BAUM -> RECHTS = NULL
SET TREE = NULL
ELSE IF TREE -> LEFT != NULL
SET TREE = BAUM -> LINKS
ANDERS
SET TREE = BAUM -> RECHTS
[ENDE VON WENN]
KOSTENLOSE TEMP
[ENDE VON WENN]
Funktion:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 