- DFA bezieht sich auf deterministische endliche Automaten. Deterministisch bezieht sich auf die Einzigartigkeit der Berechnung. Die endlichen Automaten werden deterministische endliche Automaten genannt, wenn der Maschine eine Eingabezeichenfolge Symbol für Symbol vorgelesen wird.
- In DFA gibt es nur einen Pfad für bestimmte Eingaben vom aktuellen Status zum nächsten Status.
- DFA akzeptiert die Nullverschiebung nicht, d. h. der DFA kann den Status nicht ohne Eingabezeichen ändern.
- DFA kann mehrere Endzustände enthalten. Es wird in der lexikalischen Analyse im Compiler verwendet.
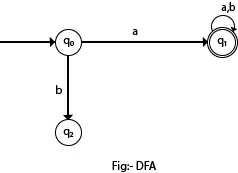
Im folgenden Diagramm sehen wir, dass es vom Zustand q0 für Eingabe a nur einen Pfad gibt, der zu q1 führt. Ebenso gibt es von q0 nur einen Pfad für Eingabe b, der zu q2 führt.
Java-Rückgabebefehl
Formale Definition von DFA
Ein DFA ist eine Sammlung von 5 Tupeln, wie wir sie in der Definition von FA beschrieben haben.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Die Übergangsfunktion kann wie folgt definiert werden:
δ: Q x ∑→Q
Grafische Darstellung von DFA
Ein DFA kann durch Digraphen dargestellt werden, die als Zustandsdiagramm bezeichnet werden. In welchem:
- Der Staat wird durch Eckpunkte dargestellt.
- Der mit einem Eingabezeichen beschriftete Bogen zeigt die Übergänge.
- Der Ausgangszustand ist mit einem Pfeil markiert.
- Der Endzustand wird durch einen Doppelkreis gekennzeichnet.
Beispiel 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Lösung:
Übergangsdiagramm:

Übergangstabelle:
| Gegenwärtiger Zustand | Nächster Zustand für Eingang 0 | Nächster Status von Eingabe 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Beispiel 2:
DFA mit ∑ = {0, 1} akzeptiert alle, die mit 0 beginnen.
Sortieren in Arraylist in Java
Lösung:

Erläuterung:
- Im obigen Diagramm können wir sehen, dass der DFA bei gegebener 0 als Eingabe für DFA im Zustand q0 seinen Zustand in q1 ändert und beim Starten von Eingabe 0 immer in den Endzustand q1 wechselt. Er kann 00, 01, 000, 001 ... akzeptieren. .usw. Es kann keine Zeichenfolge akzeptieren, die mit 1 beginnt, da es bei einer Zeichenfolge, die mit 1 beginnt, niemals in den Endzustand übergeht.
Beispiel 3:
DFA mit ∑ = {0, 1} akzeptiert alle, die mit 0 enden.
Lösung:
Gleichheit von Strings in Java

Erläuterung:
Im obigen Diagramm können wir sehen, dass der DFA bei einer gegebenen 0 als Eingabe für den DFA im Zustand q0 seinen Zustand in q1 ändert. Es kann jede Zeichenfolge akzeptieren, die mit 0 endet, wie 00, 10, 110, 100 usw. Es kann keine Zeichenfolge akzeptieren, die mit 1 endet, da es bei 1 Eingabe niemals in den Endzustand q1 wechselt, sodass die Zeichenfolge, die mit 1 endet, nicht akzeptiert oder abgelehnt wird.
