Eulerscher Pfad ist ein Pfad in einem Diagramm, der jede Kante genau einmal besucht. Der Eulersche Kreis ist ein Eulerscher Pfad, der am selben Scheitelpunkt beginnt und endet.
Benutzer MySQL anzeigen
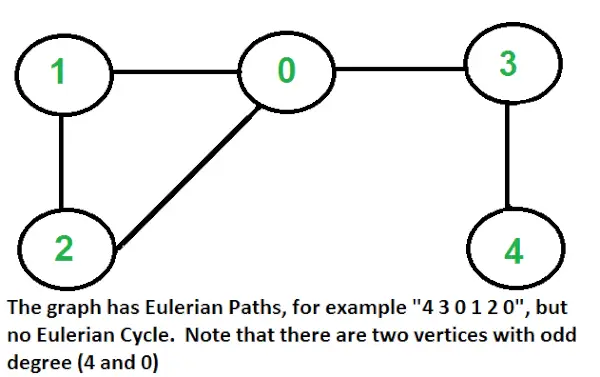


Wie finde ich heraus, ob ein gegebener Graph Eulersch ist oder nicht?
Das Problem ist das gleiche wie bei der folgenden Frage. Ist es möglich, ein bestimmtes Diagramm zu zeichnen, ohne den Bleistift vom Papier abzuheben und ohne eine der Kanten mehr als einmal nachzuzeichnen?
Ein Graph heißt Eulersch, wenn er einen Eulerschen Kreis hat, und Halbeulersch, wenn er einen Eulerschen Pfad hat. Das Problem scheint dem Hamilton-Pfad zu ähneln, der ein NP-vollständiges Problem für einen allgemeinen Graphen ist. Glücklicherweise können wir in polynomialer Zeit herausfinden, ob ein gegebener Graph einen Eulerschen Pfad hat oder nicht. Tatsächlich können wir es in O(V+E)-Zeit finden.
Im Folgenden sind einige interessante Eigenschaften ungerichteter Graphen mit einem Eulerschen Pfad und Kreis aufgeführt. Wir können diese Eigenschaften verwenden, um herauszufinden, ob ein Graph Eulersch ist oder nicht.
Eulerscher Zyklus: Ein ungerichteter Graph hat einen Eulerkreis, wenn die folgenden zwei Bedingungen zutreffen.
- Alle Eckpunkte mit einem Grad ungleich Null sind verbunden. Scheitelpunkte mit dem Grad Null interessieren uns nicht, da sie nicht zum Eulerschen Kreis oder Pfad gehören (wir berücksichtigen nur alle Kanten).
- Alle Eckpunkte haben geraden Grad.
Eulerscher Pfad: Ein ungerichteter Graph hat einen Eulerschen Pfad, wenn die folgenden zwei Bedingungen zutreffen.
- Gleich wie Bedingung (a) für den Eulerschen Zyklus.
- Wenn null oder zwei Scheitelpunkte einen ungeraden Grad haben und alle anderen Scheitelpunkte einen geraden Grad haben. Beachten Sie, dass in einem ungerichteten Diagramm nicht nur ein Knoten mit ungeradem Grad möglich ist (die Summe aller Grade ist in einem ungerichteten Diagramm immer gerade).
Beachten Sie, dass ein Graph ohne Kanten als Eulersch betrachtet wird, da es keine zu durchlaufenden Kanten gibt.
Wie funktioniert das?
Im Eulerschen Pfad gehen wir jedes Mal, wenn wir einen Scheitelpunkt v besuchen, durch zwei nicht besuchte Kanten mit einem Endpunkt als v. Daher müssen alle mittleren Scheitelpunkte im Eulerschen Pfad geraden Grad haben. Für den Eulerschen Kreis kann jeder Scheitelpunkt ein mittlerer Scheitelpunkt sein, daher müssen alle Scheitelpunkte einen geraden Grad haben.
Implementierung:
C++
// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> >int> V;>// No. of vertices> >list<>int>>*adj;>// A dynamic array of adjacency lists> public>:> >// Constructor and destructor> >Graph(>int> V) {>this>->V = V; adj =>new> list<>int>>[IN]; }> >~Graph() {>delete> [] adj; }>// To avoid memory leak> >// function to add an edge to graph> >void> addEdge(>int> v,>int> w);> >// Method to check if this graph is Eulerian or not> >int> isEulerian();> >// Method to check if all non-zero degree vertices are connected> >bool> isConnected();> >// Function to do DFS starting from v. Used in isConnected();> >void> DFSUtil(>int> v,>bool> visited[]);> };> void> Graph::addEdge(>int> v,>int> w)> {> >adj[v].push_back(w);> >adj[w].push_back(v);>// Note: the graph is undirected> }> void> Graph::DFSUtil(>int> v,>bool> visited[])> {> >// Mark the current node as visited and print it> >visited[v] =>true>;> >// Recur for all the vertices adjacent to this vertex> >list<>int>>::iterator i;> >for> (i = adj[v].begin(); i != adj[v].end(); ++i)> >if> (!visited[*i])> >DFSUtil(*i, visited);> }> // Method to check if all non-zero degree vertices are connected.> // It mainly does DFS traversal starting from> bool> Graph::isConnected()> {> >// Mark all the vertices as not visited> >bool> visited[V];> >int> i;> >for> (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) false zurückgeben; return true; } /* Die Funktion gibt einen der folgenden Werte zurück: 0 --> Wenn der Graph nicht Eulersch ist 1 --> Wenn der Graph einen Euler-Pfad hat (Semi-Eulerian) 2 --> Wenn der Graph einen Euler-Kreis hat (Eulerian) */ int Graph::isEulerian() { // Prüfen, ob alle Scheitelpunkte ungleich Null Grad verbunden sind if (isConnected() == false) return 0; // Scheitelpunkte mit ungeradem Grad zählen int odd = 0; for (int i = 0; i if (adj[i].size() & 1) odd++; // Wenn count mehr als 2 ist, ist der Graph nicht Eulersch. if (odd> 2) return 0; // If odd count ist 2, dann semi-eulerian. // Wenn die ungerade Anzahl 0 ist, dann ist die ungerade Anzahl bei ungerichteter Graphrückgabe niemals 1 : 2; // Funktion zum Ausführen von Testfällen void test(Graph &g) { int res = g.isEulerian(); if (res == 0) cout<< 'graph is not Eulerian
'; else if (res == 1) cout << 'graph has a Euler path
'; else cout << 'graph has a Euler cycle
'; } // Driver program to test above function int main() { // Let us create and test graphs shown in above figures Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); test(g1); Graph g2(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); test(g2); Graph g3(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); test(g3); // Let us create a graph with 3 vertices // connected in the form of cycle Graph g4(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); test(g4); // Let us create a graph with all vertices // with zero degree Graph g5(3); test(g5); return 0; }> |
>
>
Java
// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> >private> int> V;>// No. of vertices> >// Array of lists for Adjacency List Representation> >private> LinkedList adj[];> >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> LinkedList[v];> >for> (>int> i=>0>; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) false zurückgeben; return true; } /* Die Funktion gibt einen der folgenden Werte zurück: 0 --> Wenn der Graph nicht Eulersch ist 1 --> Wenn der Graph einen Euler-Pfad hat (Semi-Eulerian) 2 --> Wenn der Graph einen Euler-Kreis hat (Eulerian) */ int isEulerian() { // Prüfen, ob alle Scheitelpunkte ungleich Null Grad verbunden sind if (isConnected() == false) return 0; // Scheitelpunkte mit ungeradem Grad zählen int odd = 0; for (int i = 0; i if (adj[i].size()%2!=0) odd++; // Wenn count mehr als 2 ist, ist der Graph nicht Eulersch. if (odd> 2) return 0; / / Wenn die ungerade Anzahl 2 ist, dann ist die ungerade Anzahl 0, dann ist die Euler-Zahl // Beachten Sie, dass die ungerade Anzahl niemals 1 sein kann, wenn ein ungerichteter Graph zurückgegeben wird (ungerade == 2). Funktion zum Ausführen von Testfällen void test() { int res = isEulerian(); if (res == 0) System.out.println('graph is not Eulerian'); out.println('graph hat einen Euler-Pfad'); else System.out.println('graph hat einen Euler-Zyklus'); // Treibermethode public static void main(String args[]) { / / Lassen Sie uns die in den obigen Abbildungen gezeigten Diagramme erstellen und testen. Graph g1 = new Graph(5, 0); (0, 3); g1.addEdge(3, 4); g2.addEdge(0, 2); addEdge(2, 1); g2.addEdge(3, 4); g2.addEdge(4, 0); Graph g3 = new Graph(5); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Erstellen wir einen Graphen mit 3 Eckpunkten // verbunden in Form eines Zyklus Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Lassen Sie uns einen Graphen mit allen Eckpunkten // mit Null-Grad-Graph erstellen g5 = new Graph(3); g5.test(); } } // Dieser Code wurde von Aakash Hasija beigesteuert> |
>
>
Python3
# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections>import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> >def> __init__(>self>, vertices):> >self>.V>=> vertices># No. of vertices> >self>.graph>=> defaultdict(>list>)># default dictionary to store graph> ># function to add an edge to graph> >def> addEdge(>self>, u, v):> >self>.graph[u].append(v)> >self>.graph[v].append(u)> ># A function used by isConnected> >def> DFSUtil(>self>, v, visited):> ># Mark the current node as visited> >visited[v]>=> True> ># Recur for all the vertices adjacent to this vertex> >for> i>in> self>.graph[v]:> >if> visited[i]>=>=> False>:> >self>.DFSUtil(i, visited)> >'''Method to check if all non-zero degree vertices are> >connected. It mainly does DFS traversal starting from> >node with non-zero degree'''> >def> isConnected(>self>):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.V)> ># Find a vertex with non-zero degree> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i]) !>=> 0>:> >break> ># If there are no edges in the graph, return true> >if> i>=>=> self>.V>->1>:> >return> True> ># Start DFS traversal from a vertex with non-zero degree> >self>.DFSUtil(i, visited)> ># Check if all non-zero degree vertices are visited> >for> i>in> range>(>self>.V):> >if> visited[i]>=>=> False> and> len>(>self>.graph[i])>>0>:> >return> False> >return> True> >'''The function returns one of the following values> >0 -->Wenn der Graph nicht Eulersch ist> >1 -->Wenn der Graph einen Euler-Pfad hat (Semi-Eulerian)> >2 -->Wenn der Graph einen Euler-Kreis (Eulerian) hat '''> >def> isEulerian(>self>):> ># Check if all non-zero degree vertices are connected> >if> self>.isConnected()>=>=> False>:> >return> 0> >else>:> ># Count vertices with odd degree> >odd>=> 0> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i])>%> 2> !>=> 0>:> >odd>+>=> 1> >'''If odd count is 2, then semi-eulerian.> >If odd count is 0, then eulerian> >If count is more than 2, then graph is not Eulerian> >Note that odd count can never be 1 for undirected graph'''> >if> odd>=>=> 0>:> >return> 2> >elif> odd>=>=> 2>:> >return> 1> >elif> odd>>2>:> >return> 0> ># Function to run test cases> >def> test(>self>):> >res>=> self>.isEulerian()> >if> res>=>=> 0>:> >print>(>'graph is not Eulerian'>)> >elif> res>=>=> 1>:> >print>(>'graph has a Euler path'>)> >else>:> >print>(>'graph has a Euler cycle'>)> # Let us create and test graphs shown in above figures> g1>=> Graph(>5>)> g1.addEdge(>1>,>0>)> g1.addEdge(>0>,>2>)> g1.addEdge(>2>,>1>)> g1.addEdge(>0>,>3>)> g1.addEdge(>3>,>4>)> g1.test()> g2>=> Graph(>5>)> g2.addEdge(>1>,>0>)> g2.addEdge(>0>,>2>)> g2.addEdge(>2>,>1>)> g2.addEdge(>0>,>3>)> g2.addEdge(>3>,>4>)> g2.addEdge(>4>,>0>)> g2.test()> g3>=> Graph(>5>)> g3.addEdge(>1>,>0>)> g3.addEdge(>0>,>2>)> g3.addEdge(>2>,>1>)> g3.addEdge(>0>,>3>)> g3.addEdge(>3>,>4>)> g3.addEdge(>1>,>3>)> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4>=> Graph(>3>)> g4.addEdge(>0>,>1>)> g4.addEdge(>1>,>2>)> g4.addEdge(>2>,>0>)> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5>=> Graph(>3>)> g5.test()> # This code is contributed by Neelam Yadav> |
>
>
C#
// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> >private> int> V;>// No. of vertices> > >// Array of lists for Adjacency List Representation> >private> List<>int>>[]adj;> > >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> List<>int>>[in];> >for> (>int> i=0; i adj[i] = new List |
>
>
Javascript
> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> >// Constructor> >constructor(v)> >{> >this>.V = v;> >this>.adj =>new> Array(v);> >for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i |
>graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle>
Zeitkomplexität: O(V+E)
Raumkomplexität: O(V+E)
Nächste Artikel:
Eulerscher Pfad und Kreis für einen gerichteten Graphen.
Fleurys Algorithmus zum Drucken eines Eulerschen Pfades oder Kreises?
