Voraussetzung – Data Mining, Ähnlichkeitsmaß bezieht sich auf die Entfernung mit Dimensionen, die Merkmale des Datenobjekts in einem Datensatz darstellen. Wenn dieser Abstand geringer ist, liegt ein hoher Grad an Ähnlichkeit vor, ist der Abstand jedoch groß, liegt ein geringer Grad an Ähnlichkeit vor. Einige der beliebtesten Ähnlichkeitsmaße sind –
- Euklidische Entfernung.
- Manhattan-Entfernung.
- Jaccard-Ähnlichkeit.
- Minkowski-Distanz.
- Kosinusähnlichkeit.
Kosinusähnlichkeit ist eine Metrik, die dabei hilft, zu bestimmen, wie ähnlich die Datenobjekte unabhängig von ihrer Größe sind. Wir können die Ähnlichkeit zwischen zwei Sätzen in Python mithilfe der Kosinusähnlichkeit messen. Bei der Kosinusähnlichkeit werden Datenobjekte in einem Datensatz als Vektor behandelt. Die Formel zum Ermitteln der Kosinusähnlichkeit zwischen zwei Vektoren lautet:
Java-Listenknoten
(x, y) = x . y / ||x|| ||y||>
Wo,
- X . y = Produkt (Punkt) der Vektoren „x“ und „y“.||x|| Und ||und|| = Länge (Betrag) der beiden Vektoren „x“ und „y“.||x||
||und|| = reguläres Produkt der beiden Vektoren „x“ und „y“. Beispiel : Betrachten Sie ein Beispiel, um die Ähnlichkeit zwischen zwei Vektoren zu finden: 'X' Und 'Und' , unter Verwendung der Kosinusähnlichkeit. Der „x“-Vektor hat Werte, x = { 3, 2, 0, 5 } Der „y“-Vektor hat Werte, y = { 1, 0, 0, 0 } Die Formel zur Berechnung der Kosinusähnlichkeit lautet: 
(x, y) = x. y / ||x|| ||und||
Arrayliste in Java sortieren
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
Die Unähnlichkeit zwischen den beiden Vektoren „x“ und „y“ ist gegeben durch –
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- Die Kosinusähnlichkeit zwischen zwei Vektoren wird in „θ“ gemessen.
- Wenn θ = 0°, überlappen sich die Vektoren „x“ und „y“, was beweist, dass sie ähnlich sind.
- Wenn θ = 90°, sind die Vektoren „x“ und „y“ unähnlich.
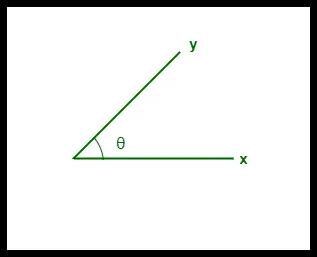
Kosinusähnlichkeit zwischen zwei Vektoren
Vorteile :
- Die Kosinusähnlichkeit ist von Vorteil, denn selbst wenn die beiden ähnlichen Datenobjekte aufgrund ihrer Größe weit um den euklidischen Abstand voneinander entfernt sind, könnten sie immer noch einen kleineren Winkel zwischen sich haben. Je kleiner der Winkel, desto größer die Ähnlichkeit.
- Bei der Darstellung in einem mehrdimensionalen Raum erfasst die Kosinusähnlichkeit die Ausrichtung (den Winkel) der Datenobjekte und nicht die Größe.