Beispiel 1:
Entwerfen Sie eine NFA für die Übergangstabelle wie unten angegeben:
| Gegenwärtiger Zustand | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | e |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Lösung:
So konvertieren Sie einen String in ein int-Java-Format
Das Übergangsdiagramm kann mithilfe der in der Tabelle angegebenen Zuordnungsfunktion gezeichnet werden.
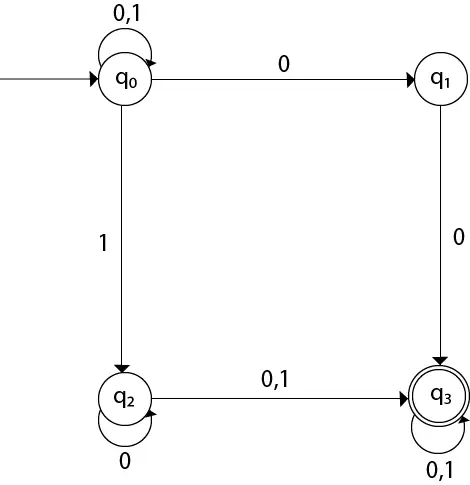
Hier,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Beispiel 2:
Entwerfen Sie einen NFA mit ∑ = {0, 1}, der alle Zeichenfolgen akzeptiert, die mit 01 enden.
Lösung:

Daher wäre NFA:

Beispiel 3:
Entwerfen Sie einen NFA mit ∑ = {0, 1}, in dem auf die doppelte „1“ die doppelte „0“ folgt.
Lösung:
Der FA mit Doppel 1 ist wie folgt:

Unmittelbar darauf sollte eine doppelte 0 folgen.
Dann,

Nun kann es vor dem Double 1 eine beliebige Zeichenfolge aus 0 und 1 geben. Ebenso kann es nach dem Double 0 eine beliebige Zeichenfolge aus 0 und 1 geben.
Daher wird die NFA zu:
thread.destroy

Betrachten wir nun die Zeichenfolge 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Beispiel 4:
Entwerfen Sie eine NFA, in der alle Zeichenfolgen eine Teilzeichenfolge 1110 enthalten.
Lösung:
Die Sprache besteht aus der gesamten Zeichenfolge, die Teilzeichenfolge 1010 enthält. Das Teilübergangsdiagramm kann wie folgt aussehen:

Nun könnte 1010 die Teilzeichenfolge sein. Daher werden wir die Eingaben Nullen und Einsen hinzufügen, damit die Teilzeichenfolge 1010 der Sprache beibehalten werden kann. Daher wird die NFA zu:

Die Übergangstabelle für das obige Übergangsdiagramm kann unten angegeben werden:
| Gegenwärtiger Zustand | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Betrachten Sie eine Zeichenfolge 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Stecken geblieben! Da es für das Eingabesymbol 0 keinen Pfad von q2 gibt, können wir die Zeichenfolge 111010 auf andere Weise verarbeiten.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Als Zustand gilt q5 als Akzeptanzzustand. Wir lassen das Ganze scannen und haben den Endzustand erreicht.
Beispiel 5:
Entwerfen Sie einen NFA mit ∑ = {0, 1}, der alle Zeichenfolgen akzeptiert, in denen das dritte Symbol von rechts immer 0 ist.
Lösung:

Somit erhalten wir das dritte Symbol von rechts immer als „0“. Die NFA kann sein:

Das obige Bild ist ein NFA, da wir im Zustand q0 mit Eingabe 0 entweder zum Zustand q0 oder q1 wechseln können.
SQL-Reihenfolge nach Zufall
