Der Ausdrucksbaum ist ein Baum, der zur Darstellung der verschiedenen Ausdrücke verwendet wird. Die Baumdatenstruktur wird zur Darstellung der Ausdrucksanweisungen verwendet. In diesem Baum bezeichnet der interne Knoten immer die Operatoren.
- Die Blattknoten bezeichnen immer die Operanden.
- Die Operationen werden immer an diesen Operanden ausgeführt.
- Der in der Tiefe des Baums vorhandene Operator hat immer die höchste Priorität.
- Der Operator, der sich nicht weit in der Tiefe des Baums befindet, hat immer die niedrigste Priorität im Vergleich zu den Operatoren, die in der Tiefe liegen.
- Der Operand wird immer in einer Tiefe des Baums vorhanden sein; daher wird es als das angesehen höchste Priorität unter allen Betreibern.
- Kurz gesagt können wir es so zusammenfassen, dass der Wert, der in einer Tiefe des Baums vorhanden ist, im Vergleich zu den anderen Operatoren, die an der Spitze des Baums vorhanden sind, die höchste Priorität hat.
- Der Hauptzweck dieser Ausdrucksbäume besteht darin, dass sie daran gewöhnt sind bewerten, analysieren Und ändern die verschiedenen Ausdrücke.
- Es wird auch verwendet, um die Assoziativität jedes Operators im Ausdruck herauszufinden.
- Beispielsweise ist der +-Operator der Links-Assoziativ und / der Rechts-Assoziativ.
- Das Dilemma dieser Assoziativität wurde durch die Verwendung des Ausdrucks Bäume gelöst.
- Diese Ausdrucksbäume werden mithilfe einer kontextfreien Grammatik gebildet.
- Wir haben jeder Grammatikproduktion eine Regel in kontextfreien Grammatiken vorangestellt.
- Diese Regeln werden auch als semantische Regeln bezeichnet, und durch die Verwendung dieser semantischen Regeln können wir die Ausdrucksbäume leicht erstellen.
- Es ist einer der Hauptbestandteile des Compiler-Designs und gehört zur Phase der semantischen Analyse.
- In dieser semantischen Analyse verwenden wir die syntaxgesteuerten Übersetzungen und erzeugen in Form einer Ausgabe den annotierten Analysebaum.
- Ein mit Anmerkungen versehener Analysebaum ist nichts anderes als die einfache Analyse, die mit dem Typattribut und jeder Produktionsregel verbunden ist.
- Das Hauptziel der Verwendung der Ausdrucksbäume besteht darin, komplexe Ausdrücke zu erstellen, die mithilfe dieser Ausdrucksbäume leicht ausgewertet werden können.
- Es ist unveränderlich und sobald wir einen Ausdrucksbaum erstellt haben, können wir ihn nicht mehr ändern oder weiter modifizieren.
- Um weitere Änderungen vorzunehmen, ist es erforderlich, den neuen Ausdrucksbaum vollständig zu erstellen.
- Es wird auch verwendet, um die Auswertung von Postfix-, Präfix- und Infix-Ausdrücken zu lösen.
Ausdrucksbäume spielen eine sehr wichtige Rolle bei der Darstellung Sprachniveau Code in Form der Daten, die hauptsächlich in der baumartigen Struktur gespeichert sind. Es wird auch in der Speicherdarstellung des verwendet Lambda Ausdruck. Mithilfe der Baumdatenstruktur können wir den Lambda-Ausdruck transparenter und expliziter ausdrücken. Es wird zunächst erstellt, um das Codesegment in das Datensegment umzuwandeln, damit der Ausdruck leicht ausgewertet werden kann.
Der Ausdrucksbaum ist ein binärer Baum, in dem jeder externe oder Blattknoten dem Operanden entspricht und jeder interne oder übergeordnete Knoten den Operatoren entspricht. Daher wäre der Ausdrucksbaum für 7 + ((1+8)*3) beispielsweise:
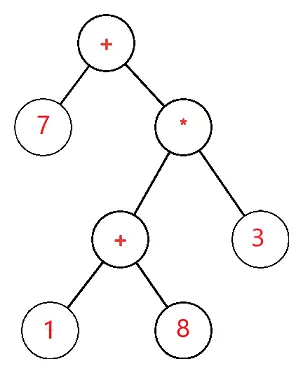
Sei S der Ausdrucksbaum
Wenn S nicht null ist, dann
Wenn S.value ein Operand ist, dann
S.Wert zurückgeben
x = lösen(S.links)
y = lösen(S.right)
Rückgabe berechne(x, y, S.Wert)
Hier im obigen Beispiel verwendete der Ausdrucksbaum kontextfreie Grammatik.
Wir haben in dieser Grammatik einige Produktionen, die mit einigen Produktionsregeln verbunden sind, hauptsächlich bekannt als Semantische Regeln . Mithilfe dieser semantischen Regeln können wir die Ergebniserzeugung aus den entsprechenden Produktionsregeln definieren. Hier haben wir den Wertparameter verwendet, der das Ergebnis berechnet und es an das Startsymbol der Grammatik zurückgibt. S.left berechnet das linke untergeordnete Element des Knotens, und auf ähnliche Weise kann das rechte untergeordnete Element des Knotens mithilfe des Parameters S.right berechnet werden.
Verwendung des Ausdrucksbaums
- Das Hauptziel der Verwendung der Ausdrucksbäume besteht darin, komplexe Ausdrücke zu erstellen, die mithilfe dieser Ausdrucksbäume leicht ausgewertet werden können.
- Es wird auch verwendet, um die Assoziativität jedes Operators im Ausdruck herauszufinden.
- Es wird auch verwendet, um die Auswertung von Postfix-, Präfix- und Infix-Ausdrücken zu lösen.
Implementierung eines Ausdrucksbaums
Um den Ausdrucksbaum zu implementieren und sein Programm zu schreiben, müssen wir eine Stapeldatenstruktur verwenden.
Da wir wissen, dass der Stapel auf dem LIFO-Prinzip „Last In First Out“ basiert, wurde das zuletzt in den Stapel verschobene Datenelement bei Bedarf herausgesprungen. Für seine Implementierung werden die beiden Hauptoperationen des Stapels, Push und Pop, verwendet. Mit der Push-Operation schieben wir das Datenelement in den Stapel und mit der Pop-Operation entfernen wir das Datenelement vom Stapel.
Hauptfunktionen des Stapels in der Ausdrucksbaumimplementierung:
Zuerst scannen wir den gegebenen Ausdruck von links nach rechts und überprüfen dann nacheinander das identifizierte Zeichen.
- Wenn ein gescanntes Zeichen ein Operand ist, wenden wir die Push-Operation an und verschieben es in den Stapel.
- Wenn ein gescanntes Zeichen ein Operator ist, wenden wir die Pop-Operation darauf an, um die beiden Werte aus dem Stapel zu entfernen und sie zu seinem untergeordneten Zeichen zu machen. Anschließend verschieben wir den aktuellen übergeordneten Knoten zurück in den Stapel.
Implementierung des Ausdrucksbaums in der Programmiersprache C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Die Ausgabe des obigen Programms ist:
X + Y * Z / W
Implementierung des Ausdrucksbaums in der Programmiersprache C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Die Ausgabe des obigen Programms ist:
X + Y * Z / W
Implementierung des Ausdrucksbaums in der Programmiersprache Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 