• Zur Erkennung von Mustern wird ein Finite-State-Automat verwendet.
• Endliche Automaten nehmen die Symbolzeichenfolge als Eingabe und ändern ihren Zustand entsprechend. Wenn in der Eingabe ein gewünschtes Symbol gefunden wird, erfolgt der Übergang.
• Während des Übergangs können die Automaten entweder in den nächsten Zustand wechseln oder im gleichen Zustand bleiben.
• FA hat zwei Zustände: den Zustand „Akzeptieren“ und den Zustand „Ablehnen“. Wenn die Eingabezeichenfolge erfolgreich verarbeitet wurde und der Automat seinen Endzustand erreicht hat, wird er akzeptiert.

Ein endlicher Automat besteht aus Folgendem:

F: endliche Menge von Zuständen
∑: endliche Menge von Eingabesymbolen
q0: Ausgangszustand
F: Endzustand
d: Übergangsfunktion

Die Übergangsfunktion kann definiert werden als

 δ: Q x ∑ →Q 

FA wird auf zwei Arten charakterisiert:

1. DFA (endliche Automaten)
2. NDFA (nicht deterministische endliche Automaten)

DFA

DFA steht für Deterministic Finite Automata. Deterministisch bezieht sich auf die Einzigartigkeit der Berechnung. In DFA geht das Eingabezeichen nur in einen Zustand. DFA akzeptiert die Nullverschiebung nicht, was bedeutet, dass der DFA den Status nicht ohne Eingabezeichen ändern kann.

DFA hat fünf Tupel {Q, ∑, q0, F, δ}

Beispiel

Sehen Sie sich ein Beispiel für deterministische endliche Automaten an:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}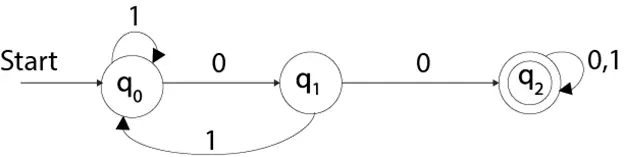 

NDFA

NDFA beziehen sich auf die nicht deterministischen endlichen Automaten. Es wird verwendet, um eine beliebige Anzahl von Zuständen für eine bestimmte Eingabe zu durchlaufen. NDFA akzeptiert die NULL-Verschiebung, was bedeutet, dass es den Status ändern kann, ohne die Symbole zu lesen.

NDFA hat ebenfalls fünf Staaten, genau wie DFA. Aber NDFA hat eine andere Übergangsfunktion.

Die Übergangsfunktion von NDFA kann wie folgt definiert werden:

Beispiel

Sehen Sie sich ein Beispiel für nicht deterministische endliche Automaten an:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}