FLOYD WARSHALL-ALGORITHMUS

Der Floyd-Warshall-Algorithmus , benannt nach seinen Schöpfern Robert Floyd und Stephen Warshall ist ein grundlegender Algorithmus in der Informatik und Graphentheorie. Es wird verwendet, um die kürzesten Pfade zwischen allen Knotenpaaren in einem gewichteten Diagramm zu finden. Dieser Algorithmus ist hocheffizient und kann mit beiden Diagrammen umgehen positiv und n negative Kantengewichte Dies macht es zu einem vielseitigen Werkzeug zur Lösung einer Vielzahl von Netzwerk- und Konnektivitätsproblemen.

Inhaltsverzeichnis

Floyd Warshall-Algorithmus
Idee hinter dem Floyd-Warshall-Algorithmus
Floyd Warshall-Algorithmus Algorithmus
Pseudocode des Floyd-Warshall-Algorithmus
Illustration des Floyd-Warshall-Algorithmus
Komplexitätsanalyse des Floyd-Warshall-Algorithmus
Warum ist der Floyd-Warshall-Algorithmus besser für dichte Graphen und nicht für spärliche Graphen?
Wichtige Interviewfragen im Zusammenhang mit Floyd-Warshall
Reale Anwendungen des Floyd-Warshall-Algorithmus

Floyd-Warshall-Algorithmus-Banner

Floyd Warshall-Algorithmus:

Der Floyd Warshall-Algorithmus ist im Gegensatz dazu ein All-Pair-Shortest-Path-Algorithmus Dijkstra Und Bellman Ford Dabei handelt es sich um Single-Source-Shortest-Path-Algorithmen. Dieser Algorithmus funktioniert sowohl für gerichtet Und ungerichtet gewichtet Grafiken. Dies funktioniert jedoch nicht für Diagramme mit negativen Zyklen (bei denen die Summe der Kanten in einem Zyklus negativ ist). Es folgt Dynamische Programmierung Ansatz, jeden möglichen Pfad zu überprüfen, der über jeden möglichen Knoten führt, um den kürzesten Abstand zwischen jedem Knotenpaar zu berechnen.
Java MVC

Idee hinter dem Floyd-Warshall-Algorithmus:

Angenommen, wir haben ein Diagramm G[][] mit IN Eckpunkte von 1 Zu N . Jetzt müssen wir a auswerten kürzestePathMatrix[][] wo ist hortestPathMatrix[i][j] stellt den kürzesten Weg zwischen Eckpunkten dar ich Und J .

Offensichtlich der kürzeste Weg dazwischen ich Zu J werde welche haben k Anzahl der Zwischenknoten. Die Idee hinter dem Floyd-Warshall-Algorithmus besteht darin, jeden einzelnen Scheitelpunkt von zu behandeln 1 Zu N als Zwischenknoten nacheinander.

Die folgende Abbildung zeigt die obige optimale Unterstruktureigenschaft im Floyd-Warshall-Algorithmus:

Floyd Warshall-Algorithmus Algorithmus:

Initialisieren Sie als ersten Schritt die Lösungsmatrix genauso wie die Eingabediagrammmatrix.
Aktualisieren Sie dann die Lösungsmatrix, indem Sie alle Scheitelpunkte als Zwischenscheitelpunkt betrachten.
Die Idee besteht darin, alle Scheitelpunkte einzeln auszuwählen und alle kürzesten Pfade zu aktualisieren, die den ausgewählten Scheitelpunkt als Zwischenscheitelpunkt im kürzesten Pfad enthalten.
Wenn wir die Scheitelpunktnummer auswählen k Als Zwischenscheitelpunkt haben wir bereits Scheitelpunkte betrachtet {0, 1, 2, .. k-1} als Zwischeneckpunkte.
Für jedes Paar (i, j) der Quell- und Zielscheitelpunkte gibt es zwei mögliche Fälle.
- k ist kein Zwischenscheitelpunkt auf dem kürzesten Weg von ich Zu J . Wir behalten den Wert von dist[i][j] wie es ist.
- k ist ein Zwischenscheitelpunkt auf dem kürzesten Weg von ich Zu J . Wir aktualisieren den Wert von dist[i][j] als dist[i][k] + dist[k][j], Wenn dist[i][j]> dist[i][k] + dist[k][j]

Pseudocode des Floyd-Warshall-Algorithmus:`>`

Für k = 0 bis n – 1
Für i = 0 bis n – 1
Für j = 0 bis n – 1
Abstand[i, j] = min(Abstand[i, j], Abstand[i, k] + Abstand[k, j])
Verzeichnis in Linux-Befehlen

wobei i = Quellknoten, j = Zielknoten, k = Zwischenknoten

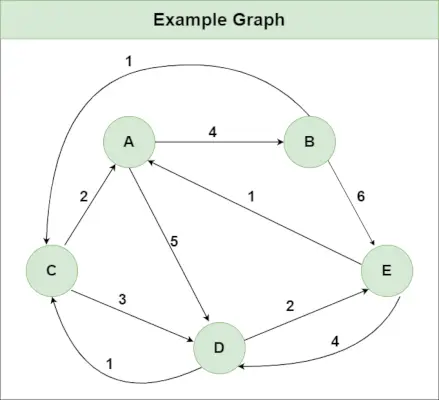
Illustration des Floyd-Warshall-Algorithmus:

Angenommen, wir haben ein Diagramm wie im Bild gezeigt:

Schritt 1 : Initialisieren Sie die Distance[][]-Matrix mithilfe des Eingabediagramms so, dass Distance[i][j]= Gewichtung der Kante von ich Zu J , auch Distance[i][j] = Infinity, wenn es keine Kante von gibt ich Zu J.

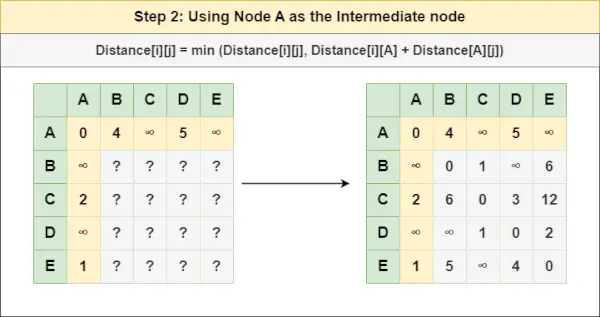
Schritt 2 : Knoten behandeln A als Zwischenknoten und berechnen Sie den Abstand[][] für jedes {i,j}-Knotenpaar mithilfe der Formel:

= Abstand[i][j] = Minimum (Abstand[i][j], (Abstand von i bis A ) + (Entfernung von A zu j ))
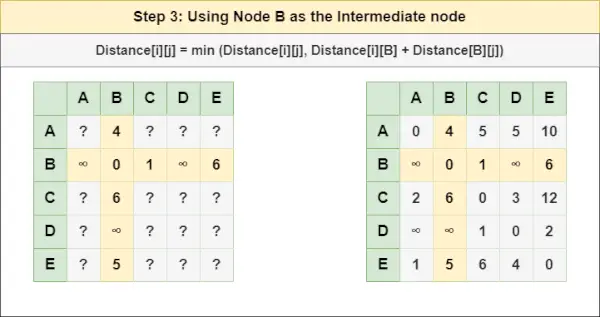
= Distanz[i][j] = Minimum (Distanz[i][j], Distanz[i][ A ] + Entfernung[ A ][J])

Schritt 3 : Knoten behandeln B als Zwischenknoten und berechnen Sie den Abstand[][] für jedes {i,j}-Knotenpaar mithilfe der Formel:

= Abstand[i][j] = Minimum (Abstand[i][j], (Abstand von i bis B ) + (Entfernung von B zu j ))
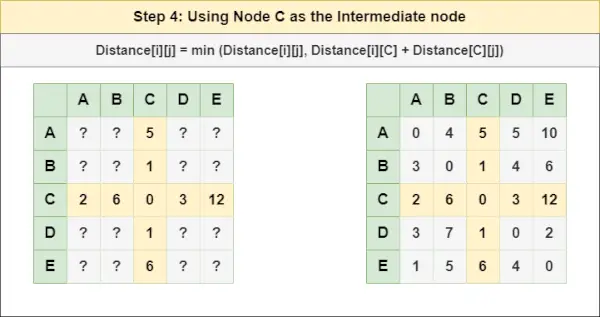
= Distanz[i][j] = Minimum (Distanz[i][j], Distanz[i][ B ] + Entfernung[ B ][J])
Softwaretests und -typen

Schritt 4 : Knoten behandeln C als Zwischenknoten und berechnen Sie den Abstand[][] für jedes {i,j}-Knotenpaar mithilfe der Formel:

= Abstand[i][j] = Minimum (Abstand[i][j], (Abstand von i bis C ) + (Entfernung von C zu j ))
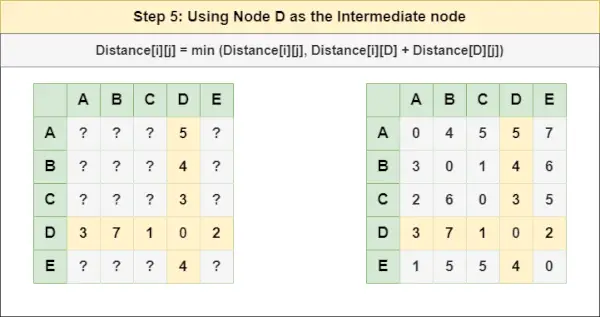
= Distanz[i][j] = Minimum (Distanz[i][j], Distanz[i][ C ] + Entfernung[ C ][J])

Schritt 5 : Knoten behandeln D als Zwischenknoten und berechnen Sie den Abstand[][] für jedes {i,j}-Knotenpaar mithilfe der Formel:

= Abstand[i][j] = Minimum (Abstand[i][j], (Abstand von i bis D ) + (Entfernung von D zu j ))
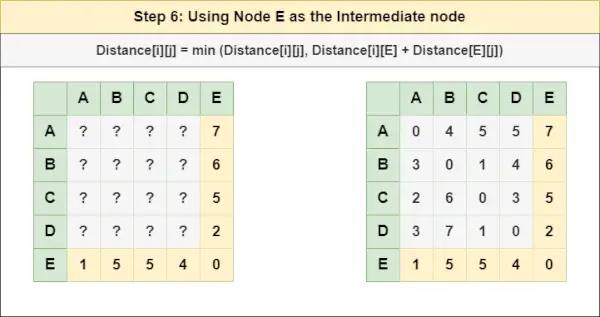
= Distanz[i][j] = Minimum (Distanz[i][j], Distanz[i][ D ] + Entfernung[ D ][J])

Schritt 6 : Knoten behandeln UND als Zwischenknoten und berechnen Sie den Abstand[][] für jedes {i,j}-Knotenpaar mithilfe der Formel:

= Abstand[i][j] = Minimum (Abstand[i][j], (Abstand von i bis UND ) + (Entfernung von UND zu j ))
= Distanz[i][j] = Minimum (Distanz[i][j], Distanz[i][ UND ] + Entfernung[ UND ][J])

Schritt 7 : Da alle Knoten als Zwischenknoten behandelt wurden, können wir jetzt die aktualisierte Distance[][]-Matrix als unsere Antwortmatrix zurückgeben.
CSS fett

Empfohlene Übung: Probieren Sie es aus!

Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:

C++

 // C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Vor Beginn einer Iteration haben wir kürzeste Abstände zwischen allen Scheitelpunktpaaren, sodass die kürzesten Abstände nur die Scheitelpunkte im Satz {0, 1, 2, .. k-1} als Zwischenscheitelpunkte berücksichtigen.  ----> Nach dem Ende einer Iteration wird die Scheitelpunkt-Nr. k wird zur Menge der Zwischeneckpunkte hinzugefügt und die Menge wird zu {0, 1, 2, .. k} */ für (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Die kürzeste Distanzmatrix drucken printSolution(dist); } /* Eine Dienstprogrammfunktion zum Drucken einer Lösung */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Funktionsaufruf floydWarshall(graph);  0 zurückgeben; } // Dieser Code wurde von Mythri J L>'> beigesteuertC(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Funktionsaufruf floydWarshall(graph);  0 zurückgeben; }>

Java

 // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Vor Beginn einer Iteration haben wir kürzeste Abstände zwischen allen Scheitelpunktpaaren, sodass die kürzesten Abstände nur die Scheitelpunkte im Satz {0, 1, 2, .. k-1} als Zwischenscheitelpunkte berücksichtigen.  ----> Nach dem Ende einer Iteration wird die Scheitelpunkt-Nr. k wird zur Menge der Zwischeneckpunkte hinzugefügt und die Menge wird zu {0, 1, 2, .. k} */ für (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Funktionsaufruf a.floydWarshall(graph);  } } // Beigetragen von Aakash Hasija>

Python3

 # Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Vor Beginn einer Iteration haben wir kürzeste Abstände zwischen allen Scheitelpunktpaaren, sodass die kürzesten Abstände nur die Scheitelpunkte in der Menge {0, 1, 2, .. k-1} als Zwischenscheitelpunkte berücksichtigen.  ----> Nach dem Ende einer Iteration wird die Scheitelpunkt-Nr. k wird zur Menge der Zwischenscheitelpunkte hinzugefügt und die Menge wird zu {0, 1, 2, .. k} ''' für k in range(V): # wähle alle Scheitelpunkte einzeln als Quelle für i in aus range(V): # Wähle alle Scheitelpunkte als Ziel für die # oben ausgewählte Quelle für j in range(V): # Wenn Scheitelpunkt k auf dem kürzesten Weg von # i nach j liegt, dann aktualisiere den Wert von dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Eine Dienstprogrammfunktion zum Drucken der Lösung def printSolution (dist): print('Folgende Matrix zeigt die kürzesten Abstände zwischen jedem Paar von Scheitelpunkten') für i in Bereich(V): für j in Bereich(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Fahrercode if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' graph = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Funktionsaufruf floydWarshall(graph) # Dieser Code wurde von Mythri J L>'> beigesteuertC#(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] graph = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Funktionsaufruf a.floydWarshall(graph);  } } // Dieser Artikel wurde von // Abdul Mateen Mohammed>'> verfasstJavascript(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var graph = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = new AllPairShortestPath();  // Lösung drucken a.floydWarshall(graph);    // Dieser Code wurde von rdtaank beigesteuert.>

PHP

  // PHP Program for Floyd Warshall Algorithm  // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm  function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix   that will finally have the shortest   distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same   as input graph matrix. Or we can say the   initial values of shortest distances are   based on shortest paths considering no   intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set   of intermediate vertices.   --->Vor Beginn einer Iteration haben wir kürzeste Abstände zwischen allen Scheitelpunktpaaren, sodass die kürzesten Abstände nur die Scheitelpunkte im Satz {0, 1, 2, .. k-1} als Zwischenscheitelpunkte berücksichtigen.   ----> Nach dem Ende einer Iteration wird die Scheitelpunkt-Nr. k wird zur Menge der Zwischenscheitelpunkte hinzugefügt und die Menge wird zu {0, 1, 2, .. k} */ für ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one  for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination  // for the above picked source  for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from  // i to j, then update the value of dist[i][j]  if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix  printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices 
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph  $V = 4 ; /* Define Infinite as a large enough  value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph   10  (0)------->(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $graph = array(array(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), array($INF, $INF, $INF, 0)); // Funktionsaufruf floydWarshall($graph, $V, $INF); // Dieser Code wurde von Ryuga beigesteuert ?>>

Ausgabe

The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Komplexitätsanalyse des Floyd-Warshall-Algorithmus:

Zeitkomplexität: O(V³), wobei V die Anzahl der Eckpunkte im Diagramm ist und wir jeweils drei verschachtelte Schleifen der Größe V ausführen
Hilfsraum: O(V²), um eine 2D-Matrix zu erstellen, um den kürzesten Abstand für jedes Knotenpaar zu speichern.

Notiz : Das obige Programm druckt nur die kürzesten Distanzen. Wir können die Lösung so modifizieren, dass die kürzesten Pfade gedruckt werden, indem wir die Vorgängerinformationen auch in einer separaten 2D-Matrix speichern.

Warum ist der Floyd-Warshall-Algorithmus besser für dichte Graphen und nicht für spärliche Graphen?

Dichtes Diagramm : Ein Diagramm, in dem die Anzahl der Kanten deutlich höher ist als die Anzahl der Eckpunkte.
Sparse-Diagramm : Ein Diagramm, in dem die Anzahl der Kanten sehr gering ist.

Egal wie viele Kanten es im Diagramm gibt Floyd Warshall-Algorithmus läuft für O(V³) Zeiten, daher ist es am besten geeignet für Dichte Diagramme . Im Fall dünnbesetzter Graphen gilt: Johnsons Algorithmus ist besser geeignet.

Wie erkennt man einen negativen Zyklus in einem Diagramm mithilfe des Floyd-Warshall-Algorithmus?
Wie unterscheidet sich der Floyd-Warshall-Algorithmus vom Dijkstra-Algorithmus?
Wie unterscheidet sich der Floyd-Warshall-Algorithmus vom Bellman-Ford-Algorithmus?

Reale Anwendungen des Floyd-Warshall-Algorithmus:

In Computernetzwerken kann der Algorithmus verwendet werden, um den kürzesten Weg zwischen allen Knotenpaaren in einem Netzwerk zu finden. Dies wird als bezeichnet Netzwerk-Routing .
Flugkonnektivität In der Luftfahrtindustrie geht es darum, den kürzesten Weg zwischen den Flughäfen zu finden.
GIS ( Geografisches Informationssystem )-Anwendungen umfassen häufig die Analyse räumlicher Daten, beispielsweise von Straßennetzen, um die kürzesten Wege zwischen Standorten zu finden.
Kleenes Algorithmus Dies ist eine Verallgemeinerung von Floyd Warshall und kann verwendet werden, um einen regulären Ausdruck für eine reguläre Sprache zu finden.