Der Grauer Code ist eine Folge binärer Zahlensysteme, die auch als bezeichnet wird reflektierter Binärcode . Der Grund für die Bezeichnung dieses Codes als reflektierter Binärcode ist der Vergleich der ersten N/2 Werte mit denen der letzten N/2 Werte in umgekehrter Reihenfolge. In diesem Code unterscheiden sich zwei aufeinanderfolgende Werte um ein Bit Binärziffer. Gray-Codes werden in der allgemeinen Folge hardwaregenerierter Binärzahlen verwendet. Diese Zahlen führen zu Mehrdeutigkeiten oder Fehlern, wenn der Übergang von einer Zahl zur nächsten erfolgt. Dieser Code löst dieses Problem einfach, indem er nur ein Bit ändert, wenn der Übergang zwischen Zahlen erfolgt.
Der Gray-Code ist ein sehr leicht gewichteter Code, da er nicht vom Wert der durch die Position angegebenen Ziffer abhängt. Dieser Code wird auch als zyklischer Variablencode bezeichnet, da der Übergang von einem Wert zu seinem nachfolgenden Wert nur eine Änderung von einem Bit mit sich bringt.
Wie generiert man Gray-Code?
Die Präfix- und Reflektionsmethode wird rekursiv verwendet, um den Gray-Code einer Zahl zu generieren. Zum Generieren von Gray-Code:
- Wir ermitteln die Anzahl der Bits, die zur Darstellung einer Zahl erforderlich sind.
- Als nächstes finden wir den Code für 0, also 0000, was dem Binärwert entspricht.
- Jetzt nehmen wir den vorherigen Code, also 0000, und ändern das höchstwertige Bit davon.
- Wir führen diesen Prozess zurückhaltend durch, bis nicht alle Codes eindeutig identifiziert sind.
- Wenn wir durch Ändern des höchstwertigen Bits den gleichen Code finden, den wir zuvor erhalten haben, wird das zweithöchstwertige Bit geändert und so weiter.
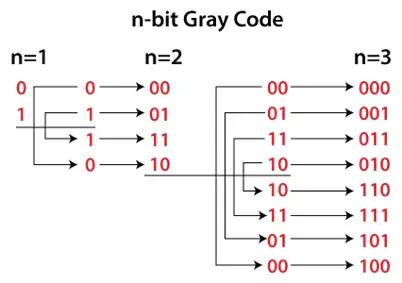
Prozess der Gray-Code-Generierung

Gray-Code-Tabelle
| Dezimalzahl | Binäre Zahl | Grauer Code |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| elf | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| fünfzehn | 1111 | 1000 |
