Die Greedy-Methode ist eine der Strategien wie „Teile und herrsche“, die zur Lösung der Probleme eingesetzt werden. Diese Methode wird zur Lösung von Optimierungsproblemen verwendet. Ein Optimierungsproblem ist ein Problem, das entweder maximale oder minimale Ergebnisse erfordert. Lassen Sie uns anhand einiger Begriffe verstehen.

Die Greedy-Methode ist der einfachste und unkomplizierteste Ansatz. Es ist kein Algorithmus, sondern eine Technik. Die Hauptfunktion dieses Ansatzes besteht darin, dass die Entscheidung auf der Grundlage der aktuell verfügbaren Informationen getroffen wird. Unabhängig davon, welche aktuellen Informationen vorliegen, wird die Entscheidung getroffen, ohne sich Gedanken über die Auswirkungen der aktuellen Entscheidung in der Zukunft machen zu müssen.

Was ist ein Benutzername?

Diese Technik wird im Wesentlichen verwendet, um die realisierbare Lösung zu bestimmen, die möglicherweise optimal ist oder nicht. Die zulässige Lösung ist eine Teilmenge, die die angegebenen Kriterien erfüllt. Die optimale Lösung ist die Lösung, die in der Teilmenge die beste und günstigste Lösung ist. Wenn im Fall der Machbarkeit mehr als eine Lösung die angegebenen Kriterien erfüllt, werden diese Lösungen als machbar betrachtet, während die optimale Lösung die beste Lösung unter allen Lösungen ist.

Merkmale der Greedy-Methode

Das Folgende sind die Merkmale einer gierigen Methode:

• Um die Lösung optimal zu konstruieren, erstellt dieser Algorithmus zwei Sätze, wobei ein Satz alle ausgewählten Elemente und ein anderer Satz die abgelehnten Elemente enthält.
• Ein Greedy-Algorithmus trifft gute lokale Entscheidungen in der Hoffnung, dass die Lösung entweder machbar oder optimal ist.

Komponenten des Greedy-Algorithmus

Die Komponenten, die im Greedy-Algorithmus verwendet werden können, sind:

Primzahl in Java

Kandidatensatz:Eine aus der Menge erstellte Lösung wird als Kandidatenmenge bezeichnet.Auswahlfunktion:Mit dieser Funktion wird der Kandidat oder die Teilmenge ausgewählt, die der Lösung hinzugefügt werden kann.Machbarkeitsfunktion:Eine Funktion, die verwendet wird, um zu bestimmen, ob der Kandidat oder die Teilmenge als Beitrag zur Lösung verwendet werden kann oder nicht.Zielfunktion:Über eine Funktion wird der Lösung bzw. Teillösung der Wert zugewiesen.Lösungsfunktion:Diese Funktion wird verwendet, um anzuzeigen, ob die vollständige Funktion erreicht wurde oder nicht.

Anwendungen des Greedy-Algorithmus

• Es wird verwendet, um den kürzesten Weg zu finden.
• Es wird verwendet, um den minimalen Spannbaum mithilfe des Prim-Algorithmus oder des Kruskal-Algorithmus zu finden.
• Es wird in einer Jobsequenzierung mit einer Frist verwendet.
• Dieser Algorithmus wird auch zur Lösung des fraktionierten Rucksackproblems verwendet.

Pseudocode des Greedy-Algorithmus

 Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } 

Das Obige ist der gierige Algorithmus. Zunächst wird der Lösung der Wert Null zugewiesen. Wir übergeben das Array und die Anzahl der Elemente im Greedy-Algorithmus. Innerhalb der for-Schleife wählen wir das Element einzeln aus und prüfen, ob die Lösung machbar ist oder nicht. Wenn die Lösung zulässig ist, führen wir die Vereinigung durch.

Lassen Sie es uns anhand eines Beispiels verstehen.

Angenommen, es gibt ein Problem „P“. Ich möchte wie folgt von A nach B reisen:

P: A → B

Das Problem ist, dass wir diese Reise von A nach B zurücklegen müssen. Es gibt verschiedene Lösungen, um von A nach B zu gelangen. Wir können von A nach B gehen zu Fuß, mit dem Auto, mit dem Fahrrad, mit der Bahn, mit dem Flugzeug usw. Es gibt eine Einschränkung bei der Reise, dass wir diese Reise innerhalb von 12 Stunden zurücklegen müssen. Nur wenn ich mit der Bahn oder dem Flugzeug fahre, kann ich diese Strecke innerhalb von 12 Stunden zurücklegen. Es gibt viele Lösungen für dieses Problem, aber nur zwei Lösungen erfüllen die Einschränkung.

Java-Sortierliste

Wenn wir sagen, dass wir die Reise zum Mindestpreis abdecken müssen. Das bedeutet, dass wir diese Distanz so gering wie möglich zurücklegen müssen, weshalb dieses Problem als Minimierungsproblem bezeichnet wird. Bisher haben wir zwei praktikable Lösungen, nämlich eine mit der Bahn und eine mit dem Flugzeug. Da das Reisen mit der Bahn zu den geringsten Kosten führt, ist es eine optimale Lösung. Eine optimale Lösung ist auch die realisierbare Lösung, liefert jedoch das beste Ergebnis, sodass diese Lösung die optimale Lösung mit den minimalen Kosten ist. Es gäbe nur eine optimale Lösung.

Das Problem, das entweder ein minimales oder ein maximales Ergebnis erfordert, wird als Optimierungsproblem bezeichnet. Die Greedy-Methode ist eine der Strategien zur Lösung von Optimierungsproblemen.

Nachteile der Verwendung des Greedy-Algorithmus

Der Greedy-Algorithmus trifft Entscheidungen auf der Grundlage der in jeder Phase verfügbaren Informationen, ohne das umfassendere Problem zu berücksichtigen. Es besteht also die Möglichkeit, dass die Greedy-Lösung nicht für jedes Problem die beste Lösung bietet.

Es folgt in jeder Phase der Wahl des lokalen Optimums mit der Absicht, das globale Optimum zu finden. Lassen Sie es uns anhand eines Beispiels verstehen.

Betrachten Sie die folgende Grafik:

Heap und Heap-Sortierung

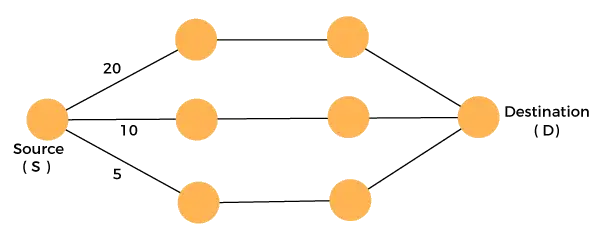
Wir müssen mit minimalen Kosten von der Quelle zum Ziel reisen. Da wir drei mögliche Lösungen mit den Kostenpfaden 10, 20 und 5 haben, ist 5 der minimale Kostenpfad und somit die optimale Lösung. Dies ist das lokale Optimum, und auf diese Weise finden wir in jeder Phase das lokale Optimum, um die globale optimale Lösung zu berechnen.