Was ist ein Hamilton-Zyklus?
Hamilton-Zyklus oder -Schaltung in einer Grafik G ist ein Zyklus, der jeden Scheitelpunkt von besucht G genau einmal und kehrt zum Startscheitelpunkt zurück.
- Wenn der Graph einen Hamiltonkreis enthält, wird er aufgerufen Hamilton-Graph sonst ist es so Nicht-Hamiltonianer .
- Es ist bekannt, einen Hamilton-Zyklus in einem Diagramm zu finden NP-vollständiges Problem , was bedeutet, dass es keinen bekannten effizienten Algorithmus gibt, um es für alle Arten von Diagrammen zu lösen. Es kann jedoch für kleine oder spezifische Diagrammtypen gelöst werden.
Das Hamilton-Zyklus-Problem hat praktische Anwendungen in verschiedenen Bereichen, wie z Logistik, Netzwerkdesign und Informatik .
Was ist der Hamilton-Pfad?
Hamilton-Pfad in einer Grafik G ist ein Pfad, der jeden Knoten von G genau einmal besucht und Hamilton-Pfad muss nicht zum Startscheitelpunkt zurückkehren. Es ist ein offener Weg.
- Ähnlich wie Hamilton-Zyklus Problem, ein zu finden Hamilton-Pfad in einem allgemeinen Diagramm ist auch NP-vollständig und kann eine Herausforderung sein. Allerdings ist es oft ein einfacheres Problem als die Suche nach einem Hamilton-Zyklus.
- Hamilton-Pfade haben Anwendungen in verschiedenen Bereichen, wie z Finden optimaler Routen in Verkehrsnetzen, Schaltungsdesign und Forschung zur Graphentheorie .
Problemerklärung: Bei einem ungerichteten Graphen besteht die Aufgabe darin, zu bestimmen, ob der Graph einen Hamiltonkreis enthält oder nicht. Wenn es enthält, wird der Pfad gedruckt.
Beispiel:
Empfohlen: Bitte lösen Sie es auf ÜBEN zuerst, bevor wir zur Lösung übergehen.Eingang: graph[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 1},{0, 1, 1, 1, 0}}
Eingabediagramm[][]
vergleichbares JavaAusgabe: {0, 1, 2, 4, 3, 0}.
Eingang: graph[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 0},{0, 1, 1, 0, 0}}
Eingabediagramm[][]
Ausgabe: Lösung existiert nicht
Naiver Algorithmus : Dieses Problem kann mit der folgenden Idee gelöst werden:
Generieren Sie alle möglichen Konfigurationen von Scheitelpunkten und drucken Sie eine Konfiguration aus, die die gegebenen Einschränkungen erfüllt. Es wird n geben! (n faktorielle) Konfigurationen. Die Gesamtzeitkomplexität dieses Ansatzes wird also sein AN!).
Hamilton-Zyklus verwenden Backtracking-Algorithmus :
Erstellen Sie ein leeres Pfadarray und fügen Sie einen Scheitelpunkt hinzu 0 dazu. Fügen Sie weitere Scheitelpunkte hinzu, beginnend mit dem Scheitelpunkt 1 . Überprüfen Sie vor dem Hinzufügen eines Scheitelpunkts, ob dieser an den zuvor hinzugefügten Scheitelpunkt angrenzt und nicht bereits hinzugefügt wurde. Wenn wir einen solchen Scheitelpunkt finden, fügen wir den Scheitelpunkt als Teil der Lösung hinzu. Wenn wir keinen Scheitelpunkt finden, kehren wir zurück FALSCH .
Abbildungen:
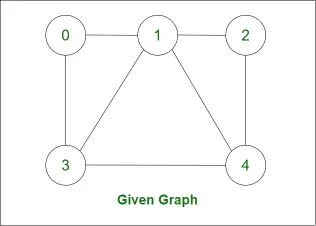
Lassen Sie uns den Hamilton-Zyklus für das folgende Diagramm herausfinden:
- Beginnen Sie mit dem Knoten 0 .
- Wenden Sie DFS an, um den Hamilton-Pfad zu finden.
- Wenn der Basisfall erreicht ist (d. h. Gesamtzahl der durchquerten Knoten == V (Gesamtscheitelpunkt) ):
- Überprüfen Sie, ob der aktuelle Knoten ein Nachbar des Startknotens ist.
- Als Knoten 2 und Knoten 0 sind keine Nachbarn voneinander, also kehren Sie von dort zurück.
Beginnend mit dem Startknoten 0, der DFS aufruft
- Da der Zyklus nicht im Pfad {0, 3, 1, 4, 2} gefunden wird. Kehren Sie also von Knoten 2 zu Knoten 4 zurück.
- Erkunden Sie nun eine andere Option für Knoten 1 (d. h. Knoten 2).
- Wenn die Grundbedingung erreicht ist, überprüfen Sie erneut den Hamilton-Kreis
- Da Knoten 4 nicht der Nachbar von Knoten 0 ist, wird der Zyklus erneut nicht gefunden und kehrt dann zurück.
- Rückkehr von Knoten 4, Knoten 2, Knoten 1.
- Erkunden Sie nun andere Optionen für Knoten 3.
Hamilton-Zyklus
- Auf dem Hamilton-Weg {0,3,4,2,1,0} Wir erhalten einen Zyklus, da Knoten 1 der Nachbar von Knoten 0 ist.
- Drucken Sie also diesen zyklischen Pfad aus.
- Dies ist unser Hamilton-Zyklus.
Nachfolgend finden Sie die Backtracking-Implementierung zum Finden des Hamilton-Zyklus:
C++ /* C++ program for solution of Hamiltonian Cycle problem using backtracking */ #include using namespace std; // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, bool graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [path[pos - 1]][ v ] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(bool graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the // last included vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate // in Hamiltonian Cycle. We don't try for 0 as // we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added // to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ bool hamCycle(bool graph[V][V]) { int *path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false ) { cout << '
Solution does not exist'; return false; } printSolution(path); return true; } /* A utility function to print solution */ void printSolution(int path[]) { cout << 'Solution Exists:' ' Following is one Hamiltonian Cycle
'; for (int i = 0; i < V; i++) cout << path[i] << ' '; // Let us print the first vertex again // to show the complete cycle cout << path[0] << ' '; cout << endl; } // Driver Code int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ bool graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ bool graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}; // Print the solution hamCycle(graph2); return 0; } // This is code is contributed by rathbhupendra> C++ #include using namespace std; int main() { cout << 'GFG!'; return 0; }> C /* C program for solution of Hamiltonian Cycle problem using backtracking */ #include // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ int isSafe(int v, int graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [ path[pos-1] ][ v ] == 0) return 0; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return 0; return 1; } /* A recursive utility function to solve hamiltonian cycle problem */ int hamCycleUtil(int graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included vertex to the // first vertex if ( graph[ path[pos-1] ][ path[0] ] == 1 ) return 1; else return 0; } // Try different vertices as a next candidate in Hamiltonian Cycle. // We don't try for 0 as we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos+1) == 1) return 1; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return 0; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[V][V]) { int path[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if ( hamCycleUtil(graph, path, 1) == 0 ) { printf('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { printf ('Solution Exists:' ' Following is one Hamiltonian Cycle
'); for (int i = 0; i < V; i++) printf(' %d ', path[i]); // Let us print the first vertex again to show the complete cycle printf(' %d ', path[0]); printf('
'); } // driver program to test above function int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamCycle(graph2); return 0; }> Java /* Java program for solution of Hamiltonian Cycle problem using backtracking */ class HamiltonianCycle { final int V = 5; int path[]; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ boolean isSafe(int v, int graph[][], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1]][v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ boolean hamCycleUtil(int graph[][], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[][]) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { System.out.println('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { System.out.println('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) System.out.print(' ' + path[i] + ' '); // Let us print the first vertex again to show the // complete cycle System.out.println(' ' + path[0] + ' '); } // driver program to test above function public static void main(String args[]) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code is contributed by Abhishek Shankhadhar> Python # Python program for solution of # hamiltonian cycle problem class Graph(): def __init__(self, vertices): self.graph = [[0 for column in range(vertices)] for row in range(vertices)] self.V = vertices ''' Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier ''' def isSafe(self, v, pos, path): # Check if current vertex and last vertex # in path are adjacent if self.graph[ path[pos-1] ][v] == 0: return False # Check if current vertex not already in path for vertex in path: if vertex == v: return False return True # A recursive utility function to solve # hamiltonian cycle problem def hamCycleUtil(self, path, pos): # base case: if all vertices are # included in the path if pos == self.V: # Last vertex must be adjacent to the # first vertex in path to make a cycle if self.graph[ path[pos-1] ][ path[0] ] == 1: return True else: return False # Try different vertices as a next candidate # in Hamiltonian Cycle. We don't try for 0 as # we included 0 as starting point in hamCycle() for v in range(1,self.V): if self.isSafe(v, pos, path) == True: path[pos] = v if self.hamCycleUtil(path, pos+1) == True: return True # Remove current vertex if it doesn't # lead to a solution path[pos] = -1 return False def hamCycle(self): path = [-1] * self.V ''' Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected ''' path[0] = 0 if self.hamCycleUtil(path,1) == False: print ('Solution does not exist
') return False self.printSolution(path) return True def printSolution(self, path): print ('Solution Exists: Following', 'is one Hamiltonian Cycle') for vertex in path: print (vertex ) # Driver Code ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) ''' g1 = Graph(5) g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,],[1, 1, 0, 0, 1], [0, 1, 1, 1, 0], ] # Print the solution g1.hamCycle(); ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) ''' g2 = Graph(5) g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,], [1, 1, 0, 0, 0], [0, 1, 1, 0, 0], ] # Print the solution g2.hamCycle(); # This code is contributed by Divyanshu Mehta> C# // C# program for solution of Hamiltonian // Cycle problem using backtracking using System; public class HamiltonianCycle { readonly int V = 5; int []path; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, int [,]graph, int []path, int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1], v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(int [,]graph, int []path, int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1],path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int [,]graph) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { Console.WriteLine('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int []path) { Console.WriteLine('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) Console.Write(' ' + path[i] + ' '); // Let us print the first vertex again // to show the complete cycle Console.WriteLine(' ' + path[0] + ' '); } // Driver code public static void Main(String []args) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int [,]graph1= {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int [,]graph2 = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code contributed by Rajput-Ji> Javascript >
PHP // PHP program for solution of // Hamiltonian Cycle problem // using backtracking $V = 5; /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ function isSafe($v, $graph, &$path, $pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if ($graph[$path[$pos - 1]][$v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for ($i = 0; $i < $pos; $i++) if ($path[$i] == $v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ function hamCycleUtil($graph, &$path, $pos) { global $V; /* base case: If all vertices are included in Hamiltonian Cycle */ if ($pos == $V) { // And if there is an edge from the // last included vertex to the first vertex if ($graph[$path[$pos - 1]][$path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point hamCycle() for ($v = 1; $v < $V; $v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe($v, $graph, $path, $pos)) { $path[$pos] = $v; /* recur to construct rest of the path */ if (hamCycleUtil($graph, $path, $pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ $path[$pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ function hamCycle($graph) { global $V; $path = array_fill(0, $V, 0); for ($i = 0; $i < $V; $i++) $path[$i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ $path[0] = 0; if (hamCycleUtil($graph, $path, 1) == false) { echo('
Solution does not exist'); return 0; } printSolution($path); return 1; } /* A utility function to print solution */ function printSolution($path) { global $V; echo('Solution Exists: Following is '. 'one Hamiltonian Cycle
'); for ($i = 0; $i < $V; $i++) echo(' '.$path[$i].' '); // Let us print the first vertex again to show the // complete cycle echo(' '.$path[0].'
'); } // Driver Code /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ $graph1 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 1), array(0, 1, 1, 1, 0), ); // Print the solution hamCycle($graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ $graph2 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 0), array(0, 1, 1, 0, 0)); // Print the solution hamCycle($graph2); // This code is contributed by mits ?>> Ausgabe
Solution Exists: Following is one Hamiltonian Cycle 0 1 2 4 3 0 Solution does not exist>
Zeitkomplexität: O(N!), wobei N die Anzahl der Eckpunkte ist.
Hilfsraum: O(1), da kein zusätzlicher Platz genutzt wird.
Notiz: Der obige Code gibt immer einen Zyklus aus, beginnend mit 0 . Der Startpunkt sollte keine Rolle spielen, da der Zyklus von jedem Punkt aus gestartet werden kann. Wenn Sie den Startpunkt ändern möchten, sollten Sie zwei Änderungen am obigen Code vornehmen.
Pfad ändern[0] = 0; Zu path[0] = s ; Wo S ist dein neues Startpunkt . Ändern Sie auch die Schleife für (int v = 1; v