Binärer Suchbaum ist eine Datenstruktur, die in der Informatik zur sortierten Organisation und Speicherung von Daten verwendet wird. Der binäre Suchbaum folgt allen Eigenschaften des Binärbaums und seiner Eigenschaften links Der untergeordnete Knoten enthält Werte, die kleiner sind als der übergeordnete Knoten und der Rechts Der untergeordnete Knoten enthält Werte, die größer sind als der übergeordnete Knoten. Diese hierarchische Struktur ermöglicht eine effiziente Suchen , Einfügen , Und Streichung Operationen an den im Baum gespeicherten Daten.
Binärer Suchbaum
Inhaltsverzeichnis
- Was ist ein binärer Suchbaum?
- Eigenschaften des binären Suchbaums
- Umgang mit doppelten Werten im binären Suchbaum
- An einem BST ausgeführte Operationen
- 1. Suche nach einem Knoten in BST
- 2. Fügen Sie einen Knoten in ein BST ein
- 3. Löschen Sie einen Knoten von BST
- 4. Durchquerung (Inorder-Durchquerung von BST)
- Anwendungen von BST
- Vorteile
- Nachteile
- FAQs (häufig gestellte Fragen) zum binären Suchbaum:
Was ist ein binärer Suchbaum?
Binärer Suchbaum (BST) ist eine besondere Art von Binärbaum wobei das linke Kind eines Knotens einen Wert hat, der kleiner ist als der Wert des Knotens, und das rechte Kind einen Wert hat, der größer als der Wert des Knotens ist. Diese Eigenschaft wird BST-Eigenschaft genannt und ermöglicht das effiziente Suchen, Einfügen und Löschen von Elementen im Baum.
Eigenschaften des binären Suchbaums:
- Der linke Teilbaum eines Knotens enthält nur Knoten mit Schlüsseln, die kleiner als der Schlüssel des Knotens sind.
- Der rechte Teilbaum eines Knotens enthält nur Knoten mit Schlüsseln, die größer als der Schlüssel des Knotens sind.
- Dies bedeutet, dass alles links von der Wurzel kleiner als der Wert der Wurzel und alles rechts von der Wurzel größer als der Wert der Wurzel ist. Aufgrund dieser Leistung ist eine binäre Suche sehr einfach.
- Der linke und rechte Teilbaum müssen jeweils ebenfalls ein binärer Suchbaum sein.
- Es dürfen keine doppelten Knoten vorhanden sein (BST kann doppelte Werte mit unterschiedlichen Behandlungsansätzen haben)
Umgang mit doppelten Werten im binären Suchbaum:
- Wir müssen durchgehend einem konsistenten Prozess folgen, d. h. entweder den doppelten Wert links oder den doppelten Wert rechts von der Wurzel speichern, aber bleiben Sie bei Ihrem Ansatz konsistent.
Grundlegende Operationen im binären Suchbaum:
1. Suche nach einem Knoten in BST:
Suchen in BST bedeutet, einen bestimmten Knoten in der Datenstruktur zu finden. Im binären Suchbaum ist das Durchsuchen eines Knotens aufgrund seiner bestimmten Reihenfolge einfach. Die Schritte zum Durchsuchen eines Knotens im binären Suchbaum sind wie folgt aufgeführt:
Typoskript-Schalter
- Vergleichen Sie zunächst das zu durchsuchende Element mit dem Wurzelelement des Baums.
- Wenn root mit dem Zielelement übereinstimmt, wird die Position des Knotens zurückgegeben.
- Wenn es nicht übereinstimmt, prüfen Sie, ob das Element kleiner als das Stammelement ist. Wenn es kleiner als das Stammelement ist, wechseln Sie zum linken Unterbaum.
- Wenn es größer als das Wurzelelement ist, wechseln Sie zum rechten Teilbaum.
- Wiederholen Sie den obigen Vorgang rekursiv, bis die Übereinstimmung gefunden wird.
- Wenn das Element nicht gefunden wird oder nicht im Baum vorhanden ist, geben Sie NULL zurück.
Lassen Sie uns nun die Suche im Binärbaum anhand eines Beispiels verstehen:
Unten ist ein BST angegeben und wir müssen nach Element 6 suchen.
Code:
Nachfolgend finden Sie die Implementierung der Suche in BST:
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->Schlüssel = Artikel; temp->left = temp->right = NULL; Rücklauftemperatur; } // Eine Dienstprogrammfunktion zum // Einfügen eines neuen Knotens mit dem angegebenen Schlüssel in BST struct node* insert(struct node* node, int key) { // Wenn der Baum leer ist, gib einen neuen Knoten zurück, wenn (node == NULL ) return newNode(key); // Andernfalls den Baum hinunter wiederholen, wenn (Schlüssel< node->key) node->left = insert(node->left, key); else if (key> node->key) node->right = insert(node->right, key); // Den (unveränderten) Knotenzeiger zurückgeben return node; } // Hilfsfunktion zum Suchen eines Schlüssels in einer BST-Struktur node* search(struct node* root, int key) root->key == key) return root; // Schlüssel ist größer als der Schlüssel von Root, wenn (root->key< key) return search(root->richtiger Schlüssel); // Schlüssel ist kleiner als der Schlüssel von Root return search(root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->Schlüssel = Artikel; temp->left = temp->right = NULL; Rücklauftemperatur; } // Eine Dienstprogrammfunktion zum // Einfügen eines neuen Knotens mit dem angegebenen Schlüssel in BST struct node* insert(struct node* node, int key) { // Wenn der Baum leer ist, gib einen neuen Knoten zurück, wenn (node == NULL ) return newNode(key); // Andernfalls den Baum hinunter wiederholen, wenn (Schlüssel< node->key) node->left = insert(node->left, key); else if (key> node->key) node->right = insert(node->right, key); // Den (unveränderten) Knotenzeiger zurückgeben return node; } // Hilfsfunktion zum Suchen eines Schlüssels in einer BST-Struktur node* search(struct node* root, int key)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); // Den (unveränderten) Knotenzeiger zurückgeben return node; } // Hilfsfunktion zum Suchen eines Schlüssels in einer BST-Knotensuche (Knotenstamm, int-Schlüssel) // Basisfälle: Stamm ist null oder Schlüssel ist am Stamm vorhanden, wenn (root == null> Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Den (unveränderten) Knotenzeiger zurückgeben. return node # Hilfsfunktion zum Suchen eines Schlüssels in einem BST def search(root, key): # Basisfälle: root ist null oder Schlüssel ist im Root vorhanden, wenn Root None ist oder root.key == key: return root # Schlüssel ist größer als der Schlüssel von Root, wenn root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Den (unveränderten) Knotenzeiger zurückgeben return node; } // Hilfsfunktion zum Suchen eines Schlüssels in einer BST-Funktion search(root, key) { // Basisfälle: root ist null oder key ist im root vorhanden, wenn (root === null || root.key === key ) { return root; } // Schlüssel ist größer als der Schlüssel von Root, wenn (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Fügen Sie einen Knoten in ein BST ein :
Am Flügel wird immer ein neuer Schlüssel eingefügt. Beginnen Sie mit der Suche nach einem Schlüssel von der Wurzel bis zu einem Blattknoten. Sobald ein Blattknoten gefunden wurde, wird der neue Knoten als untergeordnetes Element des Blattknotens hinzugefügt.
Code:
Unten ist die Implementierung des Einfügens eines einzelnen Knotens in den binären Suchbaum:
C++ // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->Schlüssel = Artikel; temp->left = temp->right = NULL; Rücklauftemperatur; } // Funktion zum Einfügen eines neuen Knotens mit // gegebenem Schlüssel in BST struct node* insert(struct node* node, int key) { // Wenn der Baum leer ist, gib einen neuen Knoten zurück, wenn (node == NULL) return newNode(key); // Andernfalls den Baum hinunter wiederholen, wenn (Schlüssel< node->key) { node->left = insert(node->left, key); } else if (key> node->key) { node->right = insert(node->right, key); } // Den Knotenzeiger zurückgeben return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->Schlüssel = Artikel; temp->left = temp->right = NULL; Rücklauftemperatur; } // Funktion zum Einfügen eines neuen Knotens mit // gegebenem Schlüssel in BST struct node* insert(struct node* node, int key) { // Wenn der Baum leer ist, gib einen neuen Knoten zurück, wenn (node == NULL) return newNode(key); // Andernfalls den Baum hinunter wiederholen, wenn (Schlüssel< node->key) { node->left = insert(node->left, key); } else if (key> node->key) { node->right = insert(node->right, key); } // Den Knotenzeiger zurückgeben return node; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Den Knoten zurückgeben return node; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Den Knotenzeiger zurückgeben return node>
Javascript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Den Knotenzeiger zurückgeben return node; }> Zeitkomplexität: O(N), wobei N die Anzahl der Knoten des BST ist
Hilfsraum: O(1)
3. Löschen Sie einen Knoten von BST :
Es wird verwendet, um einen Knoten mit einem bestimmten Schlüssel aus dem BST zu löschen und den neuen BST zurückzugeben.
Verschiedene Szenarien zum Löschen des Knotens:
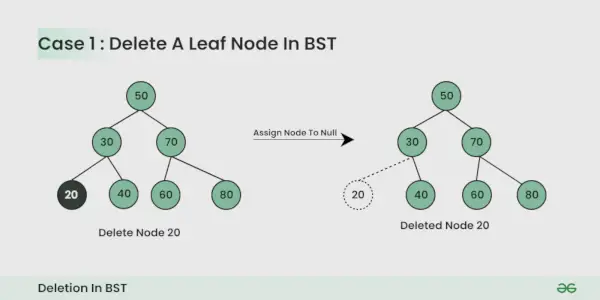
Der zu löschende Knoten ist der Blattknoten :
Es ist ganz einfach, Sie können es einfach auf Null setzen.
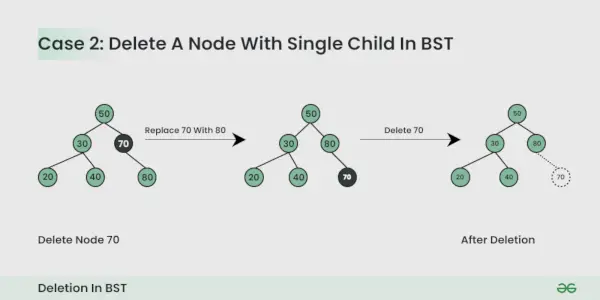
Der zu löschende Knoten hat ein Kind :
Sie können den Knoten einfach durch den untergeordneten Knoten ersetzen.
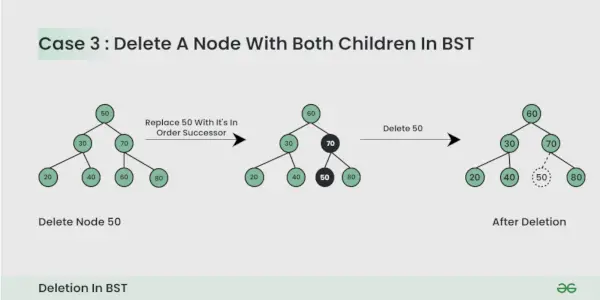
Der zu löschende Knoten hat zwei untergeordnete Knoten :
Hier müssen wir Das Löschen des Knotens erfolgt so, dass der resultierende Baum den Eigenschaften eines BST folgt. Der Trick besteht darin, den Inorder-Nachfolger des Knotens zu finden. Kopieren Sie den Inhalt des Inorder-Nachfolgers auf den Knoten und löschen Sie den Inorder-Nachfolger.
Achten Sie beim Löschen eines Knotens eines BST auf folgende Dinge:
- Sie müssen herausfinden, was der Ersatz für den zu löschenden Knoten sein wird.
- Sie wünschen sich eine minimale Störung der vorhandenen Baumstruktur
- Der Ersatzknoten kann aus dem linken oder rechten Teilbaum des gelöschten Knotens übernommen werden.
- Wenn wir if aus dem linken Teilbaum nehmen, müssen wir den größten Wert im linken Teilbaum nehmen.
- Wenn wir if aus dem rechten Teilbaum nehmen, müssen wir den kleinsten Wert im rechten Teilbaum nehmen.
Code:
Nachfolgend finden Sie die Implementierung der Löschung in BST:
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->Schlüssel = Artikel; temp->left = temp->right = NULL; Rücklauftemperatur; } // Funktion zum Einfügen eines neuen Knotens mit // gegebenem Schlüssel in BST struct node* insert(struct node* node, int key) { // Wenn der Baum leer ist, gib einen neuen Knoten zurück, wenn (node == NULL) return newNode(key); // Andernfalls den Baum hinunter wiederholen, wenn (Schlüssel< node->key) { node->left = insert(node->left, key); } else if (key> node->key) { node->right = insert(node->right, key); } // Den Knotenzeiger zurückgeben return node; } // Funktion, die den Knoten mit dem minimalen // Schlüsselwert zurückgibt, der in diesem Baum gefunden wurde struct node* minValueNode(struct node* node) { struct node* current = node; // Schleife nach unten, um das Blatt ganz links zu finden while (current && current->left != NULL) current = current->left; Rückstrom; } // Funktion, die den Schlüssel löscht und // die neue Wurzel zurückgibt struct node* deleteNode(struct node* root, int key) { // base Case if (root == NULL) return root; // Wenn der zu löschende Schlüssel // kleiner ist als der Schlüssel der Wurzel, // dann liegt er im linken Teilbaum, wenn (Schlüssel< root->key) { root->left = deleteNode(root->left, key); } // Wenn der zu löschende Schlüssel // größer ist als der Schlüssel des Roots, // dann liegt er im rechten Teilbaum else if (key> root->key) { root->right = deleteNode(root-> richtiger Schlüssel); } // Wenn der Schlüssel mit dem Schlüssel von Root identisch ist, // dann ist dies der Knoten //, der gelöscht werden soll else { // Knoten mit nur einem Kind // oder keinem Kind, wenn (root->left == NULL) { struct node* temp = root->right; frei(root); Rücklauftemperatur; } else if (root->right == NULL) { struct node* temp = root->left; frei(root); Rücklauftemperatur; } // Knoten mit zwei Kindern: // Holen Sie sich den Inorder-Nachfolger (kleinster // im rechten Teilbaum) struct node* temp = minValueNode(root->right); // Den Inhalt des Inorder-Nachfolgers // in diesen Knoten kopieren root->key = temp->key; // Den Inorder-Nachfolger löschen root->right = deleteNode(root->right, temp->key); } return root; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->Schlüssel = Artikel; temp->left = temp->right = NULL; Rücklauftemperatur; } // Funktion zum Einfügen eines neuen Knotens mit // gegebenem Schlüssel in BST struct node* insert(struct node* node, int key) { // Wenn der Baum leer ist, gib einen neuen Knoten zurück, wenn (node == NULL) return newNode(key); // Andernfalls den Baum hinunter wiederholen, wenn (Schlüssel< node->key) { node->left = insert(node->left, key); } else if (key> node->key) { node->right = insert(node->right, key); } // Den Knotenzeiger zurückgeben return node; } // Funktion, die den Knoten mit dem minimalen // Schlüsselwert zurückgibt, der in diesem Baum gefunden wurde struct node* minValueNode(struct node* node) { struct node* current = node; // Schleife nach unten, um das Blatt ganz links zu finden while (current && current->left != NULL) current = current->left; Rückstrom; } // Funktion, die den Schlüssel löscht und // den neuen Root zurückgibt struct node* deleteNode(struct node* root, int key) { // base Case if (root == NULL) return root; // Wenn der zu löschende Schlüssel // kleiner ist als der Schlüssel der Wurzel, // dann liegt er im linken Teilbaum, wenn (Schlüssel< root->key) { root->left = deleteNode(root->left, key); } // Wenn der zu löschende Schlüssel // größer ist als der Schlüssel des Roots, // dann liegt er im rechten Teilbaum else if (key> root->key) { root->right = deleteNode(root-> richtiger Schlüssel); } // Wenn der Schlüssel mit dem Schlüssel von Root identisch ist, // dann ist dies der Knoten //, der gelöscht werden soll else { // Knoten mit nur einem Kind // oder keinem Kind, wenn (root->left == NULL) { struct node* temp = root->right; frei(root); Rücklauftemperatur; } else if (root->right == NULL) { struct node* temp = root->left; frei(root); Rücklauftemperatur; } // Knoten mit zwei Kindern: // Holen Sie sich den Inorder-Nachfolger (kleinster // im rechten Teilbaum) struct node* temp = minValueNode(root->right); // Den Inhalt des Inorder-Nachfolgers // in diesen Knoten kopieren root->key = temp->key; // Den Inorder-Nachfolger löschen root->right = deleteNode(root->right, temp->key); } return root; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Den Knoten zurückgeben return node; } // Funktion, die den Knoten mit dem minimalen // Schlüsselwert zurückgibt, der in diesem Baum gefunden wurde static node minValueNode(node node) { node current = node; // Schleife nach unten, um das Blatt ganz links zu finden while (current != null && current.left != null) current = current.left; Rückstrom; } // Funktion, die den Schlüssel löscht und // den neuen statischen Root-Knoten zurückgibt deleteNode(node root, int key) { // base Case if (root == null) return root; // Wenn der zu löschende Schlüssel // kleiner ist als der Schlüssel der Wurzel, // dann liegt er im linken Teilbaum, wenn (Schlüssel< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, key); } // Wenn der Schlüssel mit dem Schlüssel von Root identisch ist, // dann ist dies der Knoten //, der gelöscht werden soll else { // Knoten mit nur einem Kind // oder keinem Kind if (root.left == null) { node temp = root.right; Rücklauftemperatur; } else if (root.right == null) { node temp = root.left; Rücklauftemperatur; } // Knoten mit zwei Kindern: // Holen Sie sich den Inorder-Nachfolger (kleinster // im rechten Teilbaum) node temp = minValueNode(root.right); // Den Inhalt des Inorder-Nachfolgers // in diesen Knoten kopieren root.key = temp.key; // Den Inorder-Nachfolger löschen root.right = deleteNode(root.right, temp.key); } return root; }> Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Den Knotenzeiger zurückgeben return root # Funktion zum Durchlaufen von BST in der Reihenfolge def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Funktion, die den Knoten mit dem minimalen # Schlüsselwert zurückgibt, der in diesem Baum gefunden wurde def minValueNode(node): current = node # Schleife nach unten, um das Blatt ganz links zu finden, während aktuell und current.left ist nicht None: current = current.left return current # Funktion, die den Schlüssel löscht und # den neuen Root zurückgibt def deleteNode(root, key): # Basisfall, wenn Root None ist: return root # Wenn der Schlüssel sein soll gelöscht ist # kleiner als der Schlüssel der Wurzel, # dann liegt er im linken Unterbaum, wenn Schlüssel< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Wenn der Schlüssel mit dem Schlüssel von Root identisch ist, # dann ist dies der Knoten, # der gelöscht werden soll, sonst: # Knoten mit nur einem Kind # oder keinem Kind Wenn root.left None ist: temp = root.right root = None return temp elif root.right ist None: temp = root.left root = None return temp # Knoten mit zwei Kindern: # Holen Sie sich den Inorder-Nachfolger (kleinster # in der rechter Teilbaum) temp = minValueNode(root.right) # Kopieren Sie den # Inhalt des Inorder-Nachfolgers in diesen Knoten root.key = temp.key # Löschen Sie den Inorder-Nachfolger root.right = deleteNode(root.right, temp.key) return root>
4. Durchquerung (Inorder-Durchquerung von BST) :
Bei binären Suchbäumen (BST) liefert die Inorder-Traversierung Knoten in nicht absteigender Reihenfolge. Wir besuchen zuerst das linke Kind, dann die Wurzel und dann das rechte Kind.
Nachfolgend finden Sie die Implementierung der Inorder-Durchquerung eines binären Suchbaums:
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->Schlüssel = Artikel; temp->left = temp->right = NULL; Rücklauftemperatur; } // Funktion zum Einfügen eines neuen Knotens mit // gegebenem Schlüssel in BST struct node* insert(struct node* node, int key) { // Wenn der Baum leer ist, gib einen neuen Knoten zurück, wenn (node == NULL) return newNode(key); // Andernfalls den Baum hinunter wiederholen, wenn (Schlüssel< node->key) { node->left = insert(node->left, key); } else if (key> node->key) { node->right = insert(node->right, key); } // Den Knotenzeiger zurückgeben return node; } // Funktion zum Durchlaufen von BST in der Reihenfolge void inorder(struct node* root) { if (root != NULL) { inorder(root->left); cout<< ' ' << root->Schlüssel; inorder(root->right); } } // Treibercode int main() { /* Lassen Sie uns folgendes BST erstellen 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // BST-Root erstellen = insert(root, 50); einfügen(Wurzel, 30); einfügen(Wurzel, 20); einfügen(Wurzel, 40); einfügen(Wurzel, 70); einfügen(Wurzel, 60); insert(root, 80); // Funktionsaufruf inorder(root); 0 zurückgeben; } // Dieser Code wurde von shivanisinghss2110>'> beigesteuertCkey); inorder(root->right); } } // Treibercode int main() { /* Lassen Sie uns folgendes BST erstellen 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // BST-Root erstellen = insert(root, 50); einfügen(Wurzel, 30); einfügen(Wurzel, 20); einfügen(Wurzel, 40); einfügen(Wurzel, 70); einfügen(Wurzel, 60); insert(root, 80); // Funktionsaufruf inorder(root); 0 zurückgeben; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Den Knoten zurückgeben return node; } // Funktion zum Durchlaufen von BST in der Reihenfolge static void inorder(node root) { if (root != null) { inorder(root.left); System.out.print(' ' + root.key); inorder(root.right); } } // Treibercode public static void main(String[] args) { /* Lassen Sie uns folgendes BST erstellen 50 / 30 70 / / 20 40 60 80 */ node root = null; // Wert 50 einfügen root = insert(root, 50); // Wert 30 einfügen insert(root, 30); // Wert 20 einfügen insert(root, 20); // Wert 40 einfügen insert(root, 40); // Wert 70 einfügen insert(root, 70); // Wert 60 einfügen insert(root, 60); // Wert 80 einfügen insert(root, 80); // die BST inorder(root) ausgeben; } } // Dieser Code wurde von abhijitjadhav1998>'> beigesteuertPython3'> beigesteuert
Ausgabe Zeitkomplexität: O(N), wobei N die Anzahl der Knoten des BST ist
Hilfsraum: O(1) Anwendungen von BST:
- Graphalgorithmen: BSTs können zur Implementierung von Graphalgorithmen verwendet werden, beispielsweise in Minimum-Spanning-Tree-Algorithmen.
- Prioritätswarteschlangen: BSTs können zur Implementierung von Prioritätswarteschlangen verwendet werden, wobei sich das Element mit der höchsten Priorität an der Wurzel des Baums befindet und Elemente mit niedrigerer Priorität in den Unterbäumen gespeichert werden.
- Selbstausgleichender binärer Suchbaum: BSTs können als selbstausgleichende Datenstrukturen wie AVL-Baum und Rot-Schwarz-Baum verwendet werden.
- Datenspeicherung und -abruf: BSTs können zum schnellen Speichern und Abrufen von Daten verwendet werden, beispielsweise in Datenbanken, wo die Suche nach einem bestimmten Datensatz in logarithmischer Zeit erfolgen kann.
Vorteile:
- Schnelle Suche: Die Suche nach einem bestimmten Wert in einem BST hat eine durchschnittliche zeitliche Komplexität von O(log n), wobei n die Anzahl der Knoten im Baum ist. Dies ist viel schneller als die Suche nach einem Element in einem Array oder einer verknüpften Liste, die im schlimmsten Fall eine zeitliche Komplexität von O(n) haben.
- Durchlauf in der Reihenfolge: BSTs können der Reihe nach durchlaufen werden, wobei der linke Teilbaum, die Wurzel und der rechte Teilbaum besucht werden. Dies kann zum Sortieren eines Datensatzes verwendet werden.
- Platzsparend: BSTs sind platzsparend, da sie im Gegensatz zu Arrays und verknüpften Listen keine redundanten Informationen speichern.
Nachteile:
- Schiefe Bäume: Wenn ein Baum schief wird, beträgt die zeitliche Komplexität von Such-, Einfügungs- und Löschvorgängen O(n) statt O(log n), was den Baum ineffizient machen kann.
- Zusätzlicher Zeitbedarf: Selbstausgleichende Bäume benötigen zusätzliche Zeit, um das Gleichgewicht während Einfüge- und Löschvorgängen aufrechtzuerhalten.
- Effizienz: BSTs sind für Datensätze mit vielen Duplikaten nicht effizient, da sie Platz verschwenden.
FAQs(Häufig gestellte Fragen)zum binären Suchbaum:
1. Was ist ein binärer Suchbaum?
Ein binärer Suchbaum (BST) ist Ein Binärbaum, in dem jeder Knoten im linken Teilbaum kleiner als die Wurzel ist und jeder Knoten im rechten Teilbaum einen Wert hat, der größer als die Wurzel ist . Die Eigenschaften eines binären Suchbaums sind rekursiv: Wenn wir einen beliebigen Knoten als Wurzel betrachten, bleiben diese Eigenschaften wahr.
2. Was ist die binäre Suchbaumoperation?
Es gibt drei Hauptoperationen im binären Suchbaum: 1. Einfügen, 2. Löschen, 3. Suchen. Aufgrund seiner Eigenschaften ist es effizient, jedes Element im binären Suchbaum zu durchsuchen.
3. Was ist ein binärer Suchbaum und ein AVL-Baum?
Binärer Suchbaum : Ein binärer Suchbaum (BST) ist ein Binärbaum, bei dem jeder Knoten im linken Teilbaum kleiner als die Wurzel ist und jeder Knoten im rechten Teilbaum einen Wert hat, der größer als die Wurzel ist.
AVL-Baum : Binäre Suchbäume (BSTs), die sich automatisch ausbalancieren und drehen, werden als AVL-Bäume bezeichnet.
4. Wozu dient der binäre Suchbaum?
Binäre Suchbäume können verwendet werden, um abstrakte Datentypen zu implementieren, wie z dynamische Sätze, Nachschlagetabellen und Prioritätswarteschlangen, und verwendet in Sortieralgorithmen wie Baumsortierung.
5. Was ist der Unterschied zwischen binärem Suchbaum und binärem Baum?
Ein binärer Suchbaum ist ein Baum, der einer bestimmten Reihenfolge folgt, um die Elemente anzuordnen, während der binäre Baum keiner Reihenfolge folgt.
In Verbindung stehende Artikel:
- Anwendung von BST
- Anwendungen, Vor- und Nachteile des binären Suchbaums
- Einfügen in den binären Suchbaum (BST)
- Suche im binären Suchbaum (BST)
- Löschen im binären Suchbaum (BST)
