Angenommen BST , die Aufgabe besteht darin, einen Knoten darin zu suchen BST .
Betrachten Sie zum Suchen eines Werts in BST diesen als sortiertes Array. Jetzt können wir ganz einfach eine Suchoperation in BST durchführen Binärer Suchalgorithmus .
Algorithmus zur Suche nach einem Schlüssel in einem bestimmten binären Suchbaum:
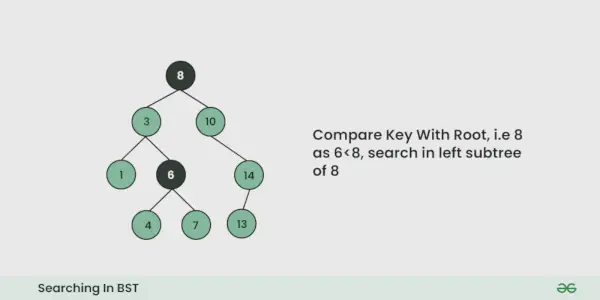
Nehmen wir an, wir möchten nach der Nummer suchen X, Wir beginnen an der Wurzel. Dann:
- Wir vergleichen den zu suchenden Wert mit dem Wert der Wurzel.
- Wenn es gleich ist, sind wir mit der Suche fertig, wenn es kleiner ist, wissen wir, dass wir zum linken Teilbaum gehen müssen, weil in einem binären Suchbaum alle Elemente im linken Teilbaum kleiner und alle Elemente im rechten Teilbaum größer sind.
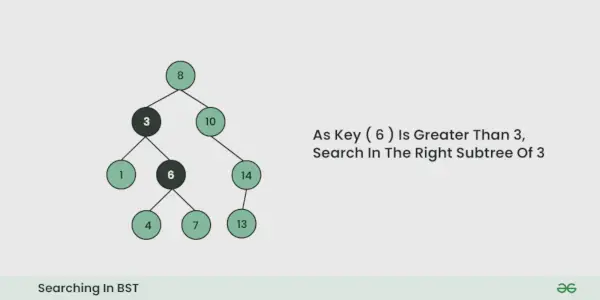
- Wiederholen Sie den obigen Schritt, bis keine Durchquerung mehr möglich ist
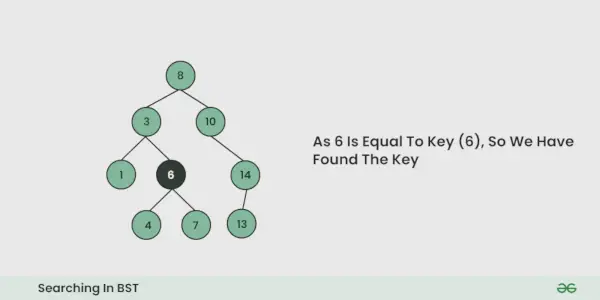
- Wenn bei einer Iteration ein Schlüssel gefunden wird, wird „True“ zurückgegeben. Sonst falsch.
Illustration der Suche in einem BST:
Zum besseren Verständnis sehen Sie sich die Abbildung unten an:
Empfohlene Übung: Suchen Sie einen Knoten in BSTT. Probieren Sie es aus!
Programm zur Implementierung der Suche in BST:
C++
Ekta Kapoor Schauspieler
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >=>new> struct> node;> >temp->key = item;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->left = insert(node->left, key);> >else> if> (key>Knoten->Schlüssel)> >node->right = insert(node->right, key);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > >// Base Cases: root is null or key is present at root> >if> (root == NULL> // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >return> 0;> }> |
>
>
C
// C function to search a given key in a given BST> #include> #include> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >= (>struct> node*)>malloc>(>sizeof>(>struct> node));> >temp->key = item;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->left = insert(node->left, key);> >else> if> (key>Knoten->Schlüssel)> >node->right = insert(node->right, key);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >return> 0;> }> |
>
Maurerformel
>
Java
// Java program to search a given key in a given BST> class> Node {> >int> key;> >Node left, right;> >public> Node(>int> item) {> >key = item;> >left = right =>null>;> >}> }> class> BinarySearchTree {> >Node root;> >// Constructor> >BinarySearchTree() {> >root =>null>;> >}> >// A utility function to insert> >// a new node with given key in BST> >Node insert(Node node,>int> key) {> >// If the tree is empty, return a new node> >if> (node ==>null>) {> >node =>new> Node(key);> >return> node;> >}> >// Otherwise, recur down the tree> >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); // Den (unveränderten) Knotenzeiger zurückgeben return node; } // Hilfsfunktion zum Suchen eines Schlüssels in einem BST Node search(Node root, int key) // Treibercode public static void main(String[] args) { BinarySearchTree tree = new BinarySearchTree(); // Knoten einfügen tree.root = tree.insert(tree.root, 50); tree.insert(tree.root, 30); tree.insert(tree.root, 20); tree.insert(tree.root, 40); tree.insert(tree.root, 70); tree.insert(tree.root, 60); tree.insert(tree.root, 80); // Zu findender Schlüssel int key = 6; // Suche in einem BST if (tree.search(tree.root, key) == null) System.out.println(key + 'notfound'); else System.out.println(key + 'found'); Schlüssel = 60; // Suche in einem BST if (tree.search(tree.root, key) == null) System.out.println(key + 'notfound'); else System.out.println(key + 'found'); } }> |
>
>
Python3
Hashmap in Java
# Python3 function to search a given key in a given BST> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> ># If the tree is empty, return a new node> >if> node>is> None>:> >return> Node(key)> ># Otherwise, recur down the tree> >if> key node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Den (unveränderten) Knotenzeiger zurückgeben. return node # Hilfsfunktion zum Suchen eines Schlüssels in einem BST def search(root, key): # Basisfälle: root ist null oder Schlüssel ist im Root vorhanden, wenn Root None ist oder root.key == key: return root # Schlüssel ist größer als der Schlüssel von root, wenn root.key return search(root.right, key) # Key ist kleiner als root 's key return search(root.left, key) # Driver Code if __name__ == '__main__': root = None root = insert(root, 50) insert(root, 30) insert(root, 20) insert (root, 40) insert(root, 70) insert(root, 60) insert(root, 80) # Zu findender Schlüssel key = 6 # Suche in einem BST, wenn search(root, key) None ist: print(key, 'nicht gefunden') else: print(key, 'found') key = 60 # Suche in einem BST, wenn search(root, key) None ist: print(key, 'notfound') else: print(key, 'found')> |
>
>
C#
// C# function to search a given key in a given BST> using> System;> public> class> Node {> >public> int> key;> >public> Node left, right;> }> public> class> BinaryTree {> >// A utility function to create a new BST node> >public> Node NewNode(>int> item)> >{> >Node temp =>new> Node();> >temp.key = item;> >temp.left = temp.right =>null>;> >return> temp;> >}> >// A utility function to insert> >// a new node with given key in BST> >public> Node Insert(Node node,>int> key)> >{> >// If the tree is empty, return a new node> >if> (node ==>null>)> >return> NewNode(key);> >// Otherwise, recur down the tree> >if> (key node.left = Insert(node.left, key); else if (key>node.key) node.right = Insert(node.right, key); // Den (unveränderten) Knotenzeiger zurückgeben return node; } // Dienstprogrammfunktion zum Suchen eines Schlüssels in einem öffentlichen BST-Knoten Search(Node root, int key) // Basisfälle: Root ist null oder Schlüssel ist im Root vorhanden, wenn (root == null // Treibercode public static void Main () { Node root = null; BinaryTree(); bt.Insert(root, 20); , 40); bt.Insert(root, 60); // Zu findender Schlüssel int key = 6; bt.Search(root, key) == null) Console.WriteLine(key + 'notfound'); else Console.WriteLine(key + 'found'); // Suche in einem BST if (bt.Search(root, key) == null) Console.WriteLine(key + 'notfound'); else Console.WriteLine(key + 'found'); |
>
// Javascript function to search a given key in a given BST>class Node {>>constructor(key) {>>this>.key = key;>>this>.left =>null>;>>this>.right =>null>;>>}>}>// A utility function to insert>// a new node with given key in BST>function>insert(node, key) {>>// If the tree is empty, return a new node>>if>(node ===>null>) {>>return>new>Node(key);>>}>>// Otherwise, recur down the tree>>if>(key node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Den (unveränderten) Knotenzeiger zurückgeben return node; } // Hilfsfunktion zum Suchen eines Schlüssels in einer BST-Funktion search(root, key) { // Basisfälle: root ist null oder key ist im root vorhanden, wenn (root === null || root.key === key ) { return root; } // Schlüssel ist größer als der Schlüssel von Root if (root.key return search(root.right, key); } // Schlüssel ist kleiner als der Schlüssel von Root return search(root.left, key); } // Treibercode let root = null; root = insert(root, 30); insert(root, 70); 60); insert(root, 80); // Zu findender Schlüssel let key = 6; // Suche in einem BST if (search(root, key) === null) { console.log(key + ' not Found'); } else { console.log(key + 'found'); } key = 60; // Suche in einem BST if (search(root, key) === null) { console.log( key + 'notfound'); } else { console.log(key + 'found');>6 not found 60 found> Zeitkomplexität: O(h), wobei h die Höhe des BST ist.
Hilfsraum: O(h), wobei h die Höhe des BST ist. Dies liegt daran, dass der maximale Speicherplatz, der zum Speichern des Rekursionsstapels benötigt wird, betragen würde H .Verwandte Links:
- Binärer Suchbaum-Einfügevorgang
- Löschvorgang für binären Suchbaum