Kleiner als Zeichen, bezeichnet als <, ist ein mathematisches Symbol, das eine Ungleichheit zwischen zwei Werten anzeigt. Wenn wir das Symbol < verwenden, bedeutet dies, dass der Wert oder die Menge auf der linken Seite kleiner ist als der Wert auf der rechten Seite.
Lass uns diskutieren Weniger als Symbol , seine Anwendungen in Ungleichungen zusammen mit einigen gelösten Beispielen.
Inhaltsverzeichnis
- Was ist ein Kleiner-als-Symbol?
- Beispiele für weniger als ein Symbol
- Tabelle der mathematischen Zeichen – kleiner als, größer als und gleich
- Wie kann man sich das Kleiner-als-Symbol merken?
- Symbole „Kleiner als“, „Größer als“ und „Gleich“.
- Kleiner als Symbol in Ungleichungen
- Weniger als symbolische Fragen
Was ist ein Kleiner-als-Symbol?
Das Kleiner-als-Zeichen (<) ist ein Symbol, das zwischen zwei Werten verwendet wird, was bedeutet, dass der linke Wert kleiner als der rechte Wert ist.
- Das Symbol < bedeutet kleiner als.
- Kleiner-als-Symbol, bezeichnet als (<) , wird verwendet, um die Beziehung zwischen zwei Zahlen oder Größen darzustellen.
- Das Kleiner-als-Symbol ist binär, das heißt, es erfordert zwei Operanden und wird als gelesen weniger als oder kleiner als.
Kleiner als Symbolbedeutung
Das Kleiner-als-Symbol (<) wird in der Mathematik verwendet, um anzuzeigen, dass der Wert auf der linken Seite des Symbols kleiner ist als der Wert auf der rechten Seite. Beispielsweise wird im Ausdruck 3<53<5 angegeben, dass 3 kleiner als 5 ist.
Beispiele für weniger als ein Symbol
Hier sind einige Beispiele für „Kleiner als Symbol“:
- 3 <5 (Drei ist weniger als fünf)
- -2 <0 (Negativ zwei ist kleiner als Null)
- 7 <7 (Sieben ist nicht weniger als sieben. Es ist gleich sieben)
Tabelle der mathematischen Zeichen – kleiner als, größer als und gleich
Die folgende Tabelle stellt die mathematischen Zeichen zum Vergleich zusammen mit ihren Namen, Bedeutungen und Beispielen dar.
| Mathematische Zeichen – Bedeutung und Beispiele | |||
|---|---|---|---|
| Symbol/Zeichen | < | = | > |
| Name | weniger als | ist gleich | größer als |
| Zeigt an | Der linke Wert ist kleiner als der rechte | Die linken und rechten Werte sind gleich | Der linke Wert ist größer als der rechte Wert |
| Beispiel | 5 <7 | 5 = 5 | 7> 5 |
Wie kann man sich das Kleiner-als-Symbol merken?
Das Zeichen „Kleiner als“ und sein Gegenstück „Größer als“ haben eine nahezu ähnliche visuelle Darstellung, jedoch in entgegengesetzter Richtung. Um Verwirrung zu vermeiden, gibt es daher zwei Tricks, mit denen wir uns merken können, was das Zeichen von „Kleiner als“ ist.
Diese Methoden werden aufgerufen L-Methode Und Methode mit kleinerem Mund.
L-Methode für Kleiner-als-Symbol
Diese Methode ist einfach – weniger als beginnt mit einem Buchstaben L, also das Symbol, das einem am ähnlichsten ist L ist derjenige, der bedeutet weniger als .
Geschlossener Mund Methode für das Kleiner-als-Symbol
Ein geschlossener Mund auf der linken Seite zeigt das Symbol „Kleiner als“ an. Das geschlossene Ende von < zeigt auf die kleinere Menge.

Symbole „Kleiner als“, „Größer als“ und „Gleich“.
Jetzt werden wir uns kurz mit den Zeichen „Größer als“, „Kleiner als“ und „Gleich“ befassen.
- Größer als Zeichen
- Weniger als Zeichen
- Gleich vorzeichen
Größer als Zeichen
Größer-als-Zeichen> wird verwendet, um einen bestimmten Vergleichstyp zwischen zwei Größen auszudrücken, bei dem der linke Wert größer als der rechte Wert ist.
Beispiel: 10> 5; (zehn ist größer als fünf)
Weniger als Zeichen
Kleiner-als-Zeichen < wird verwendet, um einen bestimmten Vergleichstyp zwischen zwei Größen auszudrücken, bei dem der linke Wert kleiner als der rechte Wert ist.
Beispiel: 5 <10; (fünf ist weniger als 10)
Gleich vorzeichen
Gleich Vorzeichen = wird verwendet, um die Gleichheit zwischen zwei Zahlen oder Werten anzuzeigen. Es drückt aus, dass sowohl der linke als auch der rechte Wert gleich sind.
Beispiel: 5 + 5 = 10, also 10 = 10 (zehn ist gleich zehn)
Oben sind die grundlegenden Zeichen aufgeführt, die zum Vergleich herangezogen werden. Es gibt auch andere Zeichen, die durch Kombination von Zeichen gebildet werden. Diese sind größer als gleich Und kleiner als gleich.
Kleiner oder gleich dem Symbol
Kleiner oder gleich Symbol ≤ wird verwendet, wenn zwischen der Größe der Menge Unklarheiten bestehen. Nehmen wir an, wir haben eine Aussage, die besagt, dass die Anzahl der Äpfel, die Ram hat, kleiner oder gleich der von Rohan ist. Dann können wir es mathematisch als x ≤ y ausdrücken, wobei x die Anzahl der Äpfel mit Ram und y die Anzahl der Äpfel mit Rohan ist.
Nicht weniger als ein Symbol
Nicht weniger als ein Symbol ≮ wird verwendet, wenn die Menge auf der linken Seite nicht kleiner ist als die Menge auf der rechten Seite. Dies bedeutet, dass die Menge auf der linken Seite entweder gleich oder größer als die Menge auf der rechten Seite ist.
Nehmen wir an, John ist „p“ Jahre alt und Andrew ist „q“ Jahre alt und John ist nicht jünger als Andrew. Das bedeutet, dass Johns Alter entweder dem Alter von Andrew entspricht oder darüber liegt. Wir können es mathematisch als p ≮ q ausdrücken.
Lesen Sie im Detail: Größer-als- und Kleiner-als-Symbole
Kleiner als Symbol in Ungleichungen
Eine Ungleichung ist eine Aussage, die zwei Ausdrücke vergleicht, und das Kleiner-als-Symbol zeigt an, dass der Ausdruck links kleiner ist als der rechte. Das Kleiner-als-Symbol wird häufig in mathematischen Ungleichungen verwendet
Arten von Ungleichheiten
Es gibt zwei Arten von Ungleichungen, die wie folgt bezeichnet werden:
- Strenge Ungleichheit
- Nichtstrikte Ungleichheit
Diese beiden Ungleichungen werden im Folgenden diskutiert:
Strikte Ungleichung (<)
Diese Art von Ungleichung stellt eine Situation dar, in der die linke Seite unbedingt kleiner ist als die rechte Seite.
Zum Beispiel:
- 2 <7
- x <10; x ist kleiner als 10, das bedeutet, dass x -∞ bis 9 sein kann
Strikte Ungleichung auf der Zahlengeraden
Um Ungleichheiten mithilfe des Kleiner-als-Symbols zu visualisieren, können Sie die Zahlen auf einer Zahlenlinie darstellen. Der Zahlenstrahl bietet eine grafische Darstellung, wie Werte miteinander verglichen werden.
Betrachten wir ein Beispiel:
x <4. Diese Ungleichung bedeutet, dass der Wert von x kleiner als 4 ist. Auf der Zahlengeraden würden Sie dies darstellen, indem Sie den Bereich links von 4 schattieren.

Nichtstrikte Ungleichung (≤)
In diesem Fall kann die linke Seite kleiner sein, aber auch gleich der rechten Seite sein.
Beispiel: 3 ≤ 3 (Drei ist kleiner oder gleich drei).
Nichtstrikte Ungleichung auf der Zahlengeraden
Betrachten wir ein Beispiel:
x ≤ 4, diese Ungleichung bedeutet, dass der Wert von x kleiner oder gleich 4 ist (einschließlich 4). Auf dem Zahlenstrahl würden Sie dies darstellen, indem Sie den Bereich links und auf der 4 schattieren.

Beispiele für weniger als ein Symbol
Hier haben wir einige Beispielfragen gelöst, damit Sie sie lernen können.
Beispiel 1: Wie stellt man symbolisch dar, dass 10 weniger als 50 ist?
Lösung:
10 ist kleiner als 50 wird symbolisch dargestellt als 10 <50
Beispiel 2: Bestimmen Sie, ob die folgenden Aussagen wahr oder falsch sind:
A) 8 <12
B) -5 <-7
C) 6 <6
Lösung:
a) Stimmt (8 ist weniger als 12)
b) False (-5 ist nicht weniger als -7)
c) Falsch (6 ist nicht kleiner als 6; sie sind gleich)
Beispiel 3: Finden Sie die mögliche ganze Zahl für „x“; wo 10
Lösung:
Gegeben, 10
Ab 10
Von x <15 kann x sein: (-∞….. 9, 10, 11, 12, 13, 14, 15)
Wenn wir den Bereich aus beiden Aussagen nehmen, erhalten wir x: 11, 12, 13, 14, 15, 16
Beispiel 4: Auflösen nach x: 3x <15
Lösung:
Um den Wert von x zu ermitteln, teilen Sie beide Seiten der Ungleichung durch 3:
3x <15
x <15 / 3
x <5
Die Lösung ist also x <5
Beispiel 5: Ein rechteckiger Garten ist 12 Fuß lang und 8 Fuß breit. Ein weiterer rechteckiger Garten ist 15 Fuß lang und 10 Fuß breit. Welcher Garten hat eine kleinere Fläche?
Lösung:
Um Flächen zu vergleichen, berechnen Sie die Flächen beider Gärten
nicht gleich MySQLDer erste Garten hat eine Fläche von 12 Fuß × 8 Fuß = 96 Quadratfuß
Der zweite Garten hat eine Fläche von 15 Fuß × 10 Fuß = 150 Quadratfuß
Wir wissen das, 96 <150
Der erste Garten hat eine kleinere Fläche, da 96 weniger als 150 ist
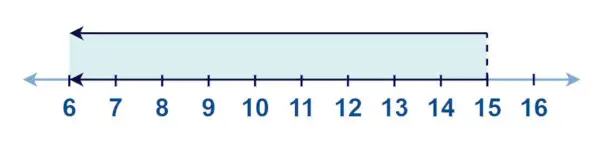
Beispiel 6: Für x <15 zeichnen Sie x auf dem Zahlenstrahl.
Lösung:
Auf der Zahlengeraden wird x <15 gezeichnet als:

Weniger als symbolische Fragen
Hier sind einige Fragen zu Less Than Sign für Ihre Praxis.
Q1. Ram hat 5 Toffees und Shyam hat 8 Toffees. Wer hat weniger Toffees?
Q2. Bob schläft jeden Tag nachmittags eine halbe Stunde und Alice schläft 60 Minuten. Wer schläft weniger?
Q3. Geben Sie an, ob die gegebene Aussage wahr oder falsch ist:
- 5 <8
- 10 <7
- x <100 ; wobei x = 20
Q4. Finden Sie die mögliche ganze Zahl für „x“; wo 5
F5. Zeichne „x“ auf dem Zahlenstrahl; wobei x <100.
F6. Platzieren Sie im Folgenden das Symbol „Größer als“ oder „Kleiner Tham“.
- 2__5
- 0,25 __ 0,252
- -14 __ 0
- 1/4 __ 1/3
Die Leute lesen auch:
- Größer-als- und Kleiner-als-Symbole
- Gleichheitszeichen
- Mehr als ein Zeichen
FAQs zu „Kleiner als Symbol“.
Was bedeutet das Kleiner-als-Zeichen in der Mathematik?
Das Kleiner-als-Zeichen (<) ist ein mathematisches Symbol, das angibt, dass der linke Wert kleiner oder von geringerer Größe als der rechte Wert ist.
Was ist das Gegenteil von „Kleiner als Symbol“?
Das Gegenteil des Kleiner-als-Symbols (), das angibt, dass ein Wert größer als der andere ist.
Wie sieht „Less Than Symbol“ aus?
Das Kleiner-als-Symbol sieht aus wie ein geneigtes „L“. Bitte beachten Sie das Bild im Artikel.
Was nützt das Kleiner-als-Zeichen?
Das Kleiner-als-Zeichen (<) wird verwendet, um anzuzeigen, dass ein Wert kleiner als ein anderer ist. Beispielsweise bedeutet die Aussage 3 < 5, dass 3 kleiner als 5 ist.
Was ist der Unterschied zwischen den Symbolen „Größer als“, „Kleiner als“ und „Gleich“?
Das Symbol „Größer als“ (>) zeigt an, dass der Wert links größer als der Wert rechts ist, während das Symbol „Kleiner als“ (<) anzeigt, dass der Wert links kleiner als der Wert rechts ist. Das Gleichheitszeichen (=) bedeutet, dass die Werte auf beiden Seiten genau gleich sind.
Kann das Kleiner-als-Symbol mit Variablen verwendet werden?
Ja, das Kleiner-als-Symbol kann bei Ungleichungen mit Variablen verwendet werden. Beispielsweise bedeutet x <10, dass die Variable x kleiner als 10 ist.
Was ist der Unterschied zwischen strengen und nicht strengen Ungleichungen?
Bei einer strikten Ungleichung (z. B. x <5) muss der linke Wert unbedingt kleiner sein als der rechte Wert. Bei einer nichtstrikten Ungleichung (z. B. x ≤ 5) kann der linke Wert gleich dem rechten Wert sein.
