Lineares Programmieren ist ein mathematisches Konzept, das verwendet wird, um die optimale Lösung der linearen Funktion zu finden. Diese Methode verwendet einfache Annahmen zur Optimierung der gegebenen Funktion. Die lineare Programmierung hat eine große praktische Anwendung und wird zur Lösung verschiedener Arten von Problemen eingesetzt.
Lineare Programmierung wird in verschiedenen Branchen eingesetzt, beispielsweise in der Schifffahrtsindustrie, der verarbeitenden Industrie, der Transportindustrie, der Telekommunikation und anderen.
Der Begriff „lineare Programmierung“ besteht aus den beiden Wörtern „linear“ und „Programmierung“. Das Wort „linear“ beschreibt die Beziehung zwischen verschiedenen Arten von Variablen vom Grad eins, die in einem Problem verwendet werden, und das Wort „Programmierung“ beschreibt die schrittweise Vorgehensweise zur Lösung dieser Probleme.
In diesem Artikel lernen wir die lineare Programmierung, ihre Beispiele, Formeln und andere Konzepte im Detail kennen.
Inhaltsverzeichnis
- Was ist lineare Programmierung?
- Komponenten der linearen Programmierung
- Beispiele für lineare Programmierung
- Probleme der linearen Programmierung
- Arten von linearen Programmierproblemen
- Lineare Programmierformel
- Wie löst man lineare Programmierprobleme?
- Lineare Programmiermethoden
- Simplex-Methode der linearen Programmierung
- Grafische Methode der linearen Programmierung
- Lineare Programmieranwendungen
- Bedeutung der linearen Programmierung
- Aktuelle Anwendungen der linearen Programmierung
- Lineare Programmierung im Operations Research
- Simplex-Methode
Was ist lineare Programmierung?
Lineares Programmieren oder Lineare Optimierung ist eine Technik, die uns hilft, die optimale Lösung für ein bestimmtes Problem zu finden. Eine optimale Lösung ist eine Lösung, die das bestmögliche Ergebnis eines bestimmten bestimmten Problems darstellt.
Vereinfacht ausgedrückt ist es die Methode herauszufinden, wie man etwas am besten macht. Bei begrenzten Ressourcen müssen Sie die Ressourcen optimal nutzen und das bestmögliche Ergebnis in Bezug auf ein bestimmtes Ziel erzielen, z. B. geringste Kosten, höchste Marge oder kürzeste Zeit.
Die Situation, die eine Suche nach den besten Werten der Variablen erfordert, die bestimmten Einschränkungen unterliegen, ist die Verwendung linearer Programmierprobleme. Diese Situationen können mit den üblichen Berechnungs- und numerischen Techniken nicht bewältigt werden.
Definition der linearen Programmierung
Lineare Programmierung ist die Technik zur Optimierung eines bestimmten Szenarios. Die Verwendung linearer Programmierung bietet uns in einer bestimmten Situation das bestmögliche Ergebnis. Es nutzt alle verfügbaren Ressourcen so, dass sie das optimale Ergebnis liefern.
Komponenten der linearen Programmierung
Die Grundkomponenten eines linearen Programmierproblems (LP) sind:
- Entscheidungsvariablen: Variablen, die Sie ermitteln möchten, um die optimale Lösung zu erreichen.
- Zielfunktion: M athematische Gleichung, die das Ziel darstellt, das Sie erreichen möchten
- Einschränkungen: Einschränkungen oder Einschränkungen, denen Ihre Entscheidungsvariablen folgen müssen.
- Nicht-Negativitätsbeschränkungen: In einigen In realen Szenarien können Entscheidungsvariablen nicht negativ sein
Zusätzliche Merkmale der linearen Programmierung
- Endlichkeit: Die Anzahl der Entscheidungsvariablen und Einschränkungen in einem LP-Problem ist endlich.
- Linearität: Die Zielfunktion und alle Einschränkungen müssen lineare Funktionen der Entscheidungsvariablen sein . Das bedeutet, dass der Grad der Variablen eins sein sollte.
Beispiele für lineare Programmierung
Anhand des unten besprochenen Beispiels können wir die Situationen verstehen, in denen die lineare Programmierung angewendet wird:
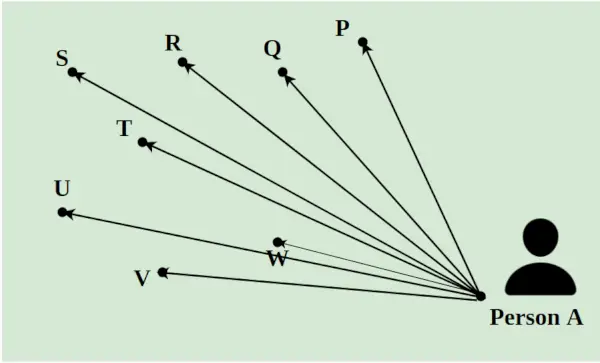
Angenommen, ein Zusteller muss täglich 8 Pakete an verschiedene Orte in einer Stadt liefern. Er muss alle Pakete von A auswählen und sie an die Punkte P, Q, R, S, T, U, V und W liefern. Der Abstand zwischen ihnen wird anhand der Linien angezeigt, wie im Bild unten gezeigt. Der kürzeste Weg, den der Zusteller einschlägt, wird mithilfe des Konzepts der linearen Programmierung berechnet.
Wie viele Städte in den USA?
Probleme der linearen Programmierung
Probleme der linearen Programmierung (LPP) Dazu gehört die Optimierung einer linearen Funktion, um die optimale Wertlösung für die Funktion zu finden. Der optimale Wert kann entweder der Maximalwert oder der Minimalwert sein.
Im LPP werden die linearen Funktionen aufgerufen Zielfunktionen. Eine Zielfunktion kann mehrere Variablen haben, die Bedingungen unterliegen und diese erfüllen müssen lineare Beschränkungen .
Arten von linearen Programmierproblemen
Es gibt viele verschiedene lineare Programmierprobleme (LPP), aber wir werden uns in diesem Artikel mit drei großen linearen Programmierproblemen befassen.
Herstellungsprobleme
Bei Herstellungsproblemen geht es um die Anzahl der Einheiten, die produziert oder verkauft werden sollten, um den Gewinn zu maximieren, wenn für jedes Produkt feste Arbeitskräfte, Maschinenstunden und Rohstoffe erforderlich sind.
Ernährungsprobleme
Es wird verwendet, um die Anzahl der verschiedenen Arten von Bestandteilen zu berechnen, die in die Ernährung aufgenommen werden müssen, um die Mindestkosten zu erzielen, abhängig von der Verfügbarkeit der Lebensmittel und deren Preisen.
Transportprobleme
Es wird zur Bestimmung des Transportplans verwendet, um die kostengünstigste Möglichkeit für den Transport eines Produkts von Werken/Fabriken an verschiedenen Standorten zu verschiedenen Märkten zu finden.
Lineare Programmierformel
Ein lineares Programmierproblem besteht aus:
- Entscheidungsvariablen
- Zielfunktion
- Einschränkungen
- Nicht-negative Einschränkungen
Entscheidungsvariablen sind die Variablen x und y, die über die Ausgabe des linearen Programmierproblems entscheiden und die endgültige Lösung darstellen.
Der Zielfunktion , im Allgemeinen durch Z dargestellt, ist die lineare Funktion, die gemäß der gegebenen Bedingung optimiert werden muss, um die endgültige Lösung zu erhalten.
Der Einschränkungen Entscheidungsvariablen auferlegte Einschränkungen, die ihre Werte begrenzen, werden als Einschränkungen bezeichnet.
Die allgemeine Formel eines linearen Programmierproblems lautet nun:
Zielfunktion : Z = ax + by
Einschränkungen: cx + dy ≥ e, px + qy ≤ r
Nicht-negative Einschränkungen: x ≥ 0, y ≥ 0
In der obigen Bedingung sind x und y die Entscheidungsvariablen.
Wie löst man lineare Programmierprobleme?
Bevor wir die linearen Programmierprobleme lösen, müssen wir zunächst die Probleme gemäß den Standardparametern formulieren. Die Schritte zur Lösung linearer Programmierprobleme sind:
Schritt 1: Markieren Sie die Entscheidungsvariablen im Problem.
Schritt 2: Erstellen Sie die Zielfunktion des Problems und prüfen Sie, ob die Funktion minimiert oder maximiert werden muss.
Schritt 3: Schreiben Sie alle Randbedingungen der linearen Probleme auf.
Schritt 4: Stellen Sie sicher, dass die Entscheidungsvariablen nichtnegativ eingeschränkt sind.
Schritt 5: Lösen Sie nun das Problem der linearen Programmierung mit einer beliebigen Methode. Im Allgemeinen verwenden wir entweder die Simplex- oder die grafische Methode.
Lineare Programmiermethoden
Wir verwenden verschiedene Methoden zur Lösung linearer Programmierprobleme. Die beiden am häufigsten verwendeten Methoden sind:
- Simplex-Methode
- Grafische Methode
Lassen Sie uns in diesem Artikel mehr über diese beiden Methoden erfahren.
Simplex-Methode der linearen Programmierung
Eine der gebräuchlichsten Methoden zur Lösung des linearen Programmierproblems ist die Simplex-Methode. Bei dieser Methode wiederholen wir eine bestimmte Bedingung „n“ mehrmals, bis eine optimale Lösung erreicht ist.
Die Schritte, die zur Lösung linearer Programmierprobleme mit der Simplex-Methode erforderlich sind, sind:
Schritt 1: Formulieren Sie die linearen Programmierprobleme basierend auf den gegebenen Randbedingungen.
Schritt 2: Wandeln Sie alle gegebenen Ungleichungen in Gleichungen oder Gleichungen der linearen Programmierprobleme um, indem Sie bei Bedarf die Slack-Variable zu jeder Ungleichung hinzufügen.
Schritt 3: Konstruieren Sie die anfängliche Simplex-Tabelle. Indem Sie jede Einschränkungsgleichung in einer Zeile darstellen und die Zielfunktion in die untere Zeile schreiben. Die so erhaltene Tabelle wird Simplex-Tabelle genannt.
Schritt 4: Identifizieren Sie den größten negativen Eintrag in der unteren Zeile. Die Spalte des Elements mit dem höchsten negativen Eintrag wird als Pivot-Spalte bezeichnet
Schritt 5: Teilen Sie die Einträge der Spalte ganz rechts durch die Einträge der jeweiligen Pivot-Spalte, ohne die Einträge der untersten Zeile. Jetzt wird die Zeile mit den wenigsten Einträgen als Pivotzeile bezeichnet. Das Pivot-Element ergibt sich aus dem Schnittpunkt der Pivot-Zeile und der Pivot-Spalte.
Schritt 6: Setzen Sie mithilfe der Matrixoperation und mithilfe des Pivot-Elements alle Einträge in der Pivot-Spalte auf Null.
Schritt 7: Suchen Sie nach nicht-negativen Einträgen in der untersten Zeile. Wenn in der untersten Zeile keine negativen Einträge vorhanden sind, beenden Sie den Vorgang, andernfalls starten Sie den Vorgang erneut ab Schritt 4.
Schritt 8: Die so erhaltene endgültige Simplex-Tabelle liefert die Lösung unseres Problems.
Grafische Methode der linearen Programmierung
Die grafische Methode ist eine andere Methode als die Simplex-Methode, die zur Lösung linearer Programmierprobleme verwendet wird. Wie der Name schon sagt, verwendet diese Methode Graphen, um die gegebenen linearen Programmierprobleme zu lösen. Dies ist die beste Methode zur Lösung linearer Programmierprobleme und erfordert weniger Aufwand als die Simplex-Methode.
Mit dieser Methode zeichnen wir alle Ungleichungen auf, die in den gegebenen linearen Programmierproblemen Einschränkungen unterliegen. Sobald alle Ungleichungen des gegebenen LPP im XY-Graphen aufgetragen sind, ergibt der gemeinsame Bereich aller Ungleichungen die optimale Lösung. Alle Eckpunkte des zulässigen Bereichs werden berechnet und der Wert der Zielfunktion an allen diesen Punkten wird berechnet. Durch den Vergleich dieser Werte erhalten wir die optimale Lösung des LPP.
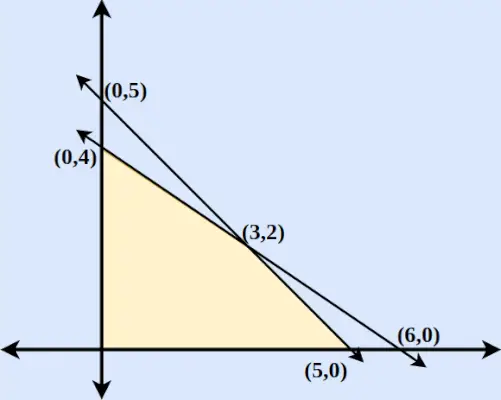
Beispiel: Finden Sie den maximalen und minimalen Wert von z = 6x + 9y, wenn die Randbedingungen lauten:
- 2x + 3y ≤ 12
- x und y ≥ 0
- x + y ≤ 5
Lösung:
Schritt 1 : Wandeln Sie zunächst die Ungleichungen in Normalgleichungen um. Daher lauten die Gleichungen 2x+3y = 0, x = 0, y = 0 und x + y = 5.
Schritt 2 : Finden Sie die Punkte, an denen 2x + 3y und x + y = 5 die x-Achse und die y-Achse schneiden. Um den Schnittpunkt der x-Achse zu finden, setzen Sie y = 0 in die entsprechende Gleichung ein und ermitteln Sie den Punkt. In ähnlicher Weise setzen Sie für die Schnittpunkte der y-Achse x = 0 in die entsprechende Gleichung ein.
Schritt 3 : Zeichnen Sie die beiden Linien, die die x-Achse und die y-Achse schneiden. Wir stellen fest, dass sich die beiden Achsen bei (3,2) schneiden.
Schritt 4 : Für x ≥ 0 und y ≥ 0 finden wir, dass beide Ungleichungen befolgt werden. Daher umfasst die Region einen Flächenbereich, der von zwei Achsen und beiden Linien einschließlich des Ursprungs umschlossen wird. Der dargestellte Bereich ist unten in der Abbildung dargestellt.
Schritt 5 : Finden Sie Z für jeden Punkt sowie Maxima und Minima.
Koordinaten Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3.2) Z = 36 Daher finden wir, dass Z = 6x + 9y bei (0,5) maximal und bei (5,0) minimal ist.
Lineare Programmieranwendungen
Die lineare Programmierung findet in verschiedenen Bereichen Anwendung. Es wird verwendet, um die minimalen Kosten eines Prozesses zu ermitteln, wenn alle Randbedingungen der Probleme gegeben sind. Es wird verwendet, um die Transportkosten des Fahrzeugs usw. zu optimieren. Es gibt verschiedene Anwendungen der linearen Programmierung
Maschinenbauindustrie
Die Maschinenbauindustrie nutzt lineare Programmierung, um Konstruktions- und Fertigungsprobleme zu lösen und aus einer gegebenen Bedingung die maximale Leistung zu erzielen.
Fertigungsindustrien
Fertigungsindustrien nutzen lineare Programmierung, um den Gewinn der Unternehmen zu maximieren und die Herstellungskosten zu senken.
Energiewirtschaft
Energieunternehmen nutzen lineare Programmierung, um ihre Produktionsleistung zu optimieren.
Transportindustrie
Lineare Programmierung wird auch in der Transportbranche eingesetzt, um einen Weg zur Minimierung der Transportkosten zu finden.
Bedeutung der linearen Programmierung
Die lineare Programmierung ist in verschiedenen Branchen von großer Bedeutung. Sie maximiert den Ausgabewert und minimiert gleichzeitig die Eingabewerte entsprechend verschiedenen Einschränkungen.
LP ist sehr gut anwendbar, wenn wir beim Lösen eines Problems mehrere Bedingungen haben und die Ausgabe des Problems optimieren müssen, d. h. wir müssen entweder den minimalen oder den maximalen Wert entsprechend einer bestimmten Bedingung finden.
Mehr lesen,
- Lineare Ungleichungen
- Algebraische Lösung linearer Ungleichungen
Probleme der linearen Programmierung
Problem 1: Ein Unternehmen produziert und verkauft zwei Arten von Produkten und die Produktionskosten für jede Einheit a und b betragen 200 bzw. 150 Rupien. Jede Produkteinheit bringt einen Gewinn von 20 Rupien und jede Produkteinheit b bringt beim Verkauf einen Gewinn von 15 Rupien . Das Unternehmen schätzt, dass die monatliche Nachfrage von A und B maximal der geernteten Einheit entspricht. Das Produktionsbudget für den Monat ist auf 50.000 Rupien festgelegt. Wie viele Einheiten sollte das Unternehmen herstellen, um den maximalen Gewinn aus seinen monatlichen Verkäufen von a zu erzielen? und B?
Lösung:
Sei x = Anzahl der Einheiten vom Typ A
y = Anzahl der Einheiten vom Typ B
Maximieren Sie Z = 40x + 50y
Vorbehaltlich der Einschränkungen
3x + y ≤ 9
x + 2y ≤ 8
und x, y ≥ 0
Betrachten Sie die Gleichung,
3x + y = 9
x = 3
y = 0
und x + 2y = 8
x = 8
y = 0
Jetzt können wir den Maximalwert von Z bestimmen, indem wir den Wert von Z an den vier Punkten (Eckpunkten) auswerten, wie unten gezeigt
Eckpunkte
Z = 40x + 50y
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Maximaler Gewinn, Z = Rs. 230
∴ Die Anzahl der Einheiten vom Typ A beträgt 2 und die Anzahl der Einheiten vom Typ B beträgt 3.
Typoskript-Pfeilfunktion
Problem 2: Maximieren Sie Z = 3x + 4y.
Vorbehaltlich der Einschränkungen gilt: x + y ≤ 450, 2x + y ≤ 600 und x, y ≤ 0.
Lösung:
Wir haben aus dem Gegebenen
Einschränkungen (1)
X + Y = 450
Setzt man x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Setzen wir y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Aus, Einschränkungen (2)
2x + y = 600
Setzt man x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Setzen wir y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Jetzt haben wir die Punktkoordinate Z = 3x + 4y
| Eckpunkte | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Daher ist das optimale Lösungsmaximum Z = 1800 bei den Koordinaten x = 0 und y = 450. Die Grafik ist unten dargestellt.

Aktuelle Anwendungen der linearen Programmierung
Lineare Programmierung, eine leistungsstarke mathematische Technik, wird zur Lösung von Optimierungsproblemen in verschiedenen Branchen eingesetzt. Hier sind einige moderne Anwendungen:
- Optimierung der Lieferkette : Lineare Programmierung hilft Unternehmen, Kosten zu minimieren und die Effizienz in ihren Lieferketten zu maximieren. Es wird zur Ermittlung der kostengünstigsten Transportwege, Lagerabläufe und Bestandsverwaltungsstrategien verwendet.
- Energiemanagement : Im Energiesektor wird die lineare Programmierung genutzt, um den Mix der Energieerzeugungsmethoden zu optimieren. Dazu gehört das Gleichgewicht zwischen traditionellen und erneuerbaren Energiequellen, um Kosten und Umweltbelastungen zu reduzieren und gleichzeitig die Nachfrage zu decken.
- Design von Telekommunikationsnetzwerken : Lineare Programmierung hilft beim Entwurf effizienter Telekommunikationsnetze. Es hilft bei der Zuweisung von Bandbreite, dem Entwurf von Netzwerklayouts und der Optimierung des Datenflusses, um eine Hochgeschwindigkeitskommunikation zu geringeren Kosten sicherzustellen.
- Finanzielle Planung : Unternehmen und Finanzanalysten nutzen lineare Programmierung zur Portfoliooptimierung, zum Risikomanagement und zur Kapitalbudgetierung. Es hilft bei Anlageentscheidungen, die die Rendite maximieren und gleichzeitig das Risiko minimieren.
- Gesundheitslogistik : Im Gesundheitswesen wird lineare Programmierung eingesetzt, um die Zuweisung von Ressourcen wie Krankenhausbetten, medizinischem Personal und Ausrüstung zu optimieren. Dies ist von entscheidender Bedeutung, um die Patientenversorgung zu verbessern, Wartezeiten zu verkürzen und die Kosten effektiv zu verwalten.
- Optimierung des Fertigungsprozesses : Lineare Programmierung wird verwendet, um das optimale Produktionsniveau für mehrere Produkte innerhalb einer Produktionsanlage unter Berücksichtigung von Einschränkungen wie Arbeitskräften, Materialien und Maschinenverfügbarkeit zu bestimmen.
- Agrarplanung : Landwirte und Agrarplaner nutzen lineare Programmierung, um über die Auswahl der Pflanzen, die Landnutzung und die Ressourcenzuteilung zu entscheiden, um Erträge und Gewinne zu maximieren und gleichzeitig Ressourcen zu schonen.
- Planung der Flugbesatzung : Fluggesellschaften nutzen lineare Programmierung, um ihre Besatzungen effizient zu planen, sicherzustellen, dass die Flüge vorschriftsmäßig besetzt sind und die Betriebskosten minimiert werden.
Diese Anwendungen demonstrieren die Vielseitigkeit und Leistungsfähigkeit der linearen Programmierung bei der Lösung komplexer Optimierungsprobleme in verschiedenen Sektoren und verdeutlichen ihre Relevanz in der heutigen datengesteuerten Welt.
Lineare Programmierung im Operations Research
- Kernwerkzeug : Lineare Programmierung ist ein grundlegendes Werkzeug im Operations Research zur Ressourcenoptimierung.
- Entscheidungsfindung : Hilft dabei, die besten Entscheidungen hinsichtlich der Ressourcenzuteilung, Gewinnmaximierung oder Kostenminimierung zu treffen.
- Breite Anwendungen : Wird in verschiedenen Bereichen wie Logistik, Fertigung, Finanzen und Gesundheitswesen zur Lösung komplexer Probleme eingesetzt.
- Modellierung realer Probleme : Wandelt reale Probleme in mathematische Modelle um, um die effizientesten Lösungen zu finden.
Simplex-Methode
- Optimierungsalgorithmus : Die Simplex-Methode ist ein leistungsstarker Algorithmus, der in der linearen Programmierung verwendet wird, um die optimale Lösung für lineare Ungleichungen zu finden.
- Schritt-für-Schritt-Ansatz : Es bewegt sich iterativ auf die beste Lösung zu, indem es durch die Kanten des durch Einschränkungen definierten zulässigen Bereichs navigiert.
- Effizienz : Bekannt für seine Effizienz bei der Lösung umfangreicher linearer Programmierprobleme.
- Vielseitigkeit : Anwendbar in verschiedenen Bereichen wie Diätplanung, Netzwerkabläufen, Produktionsplanung und mehr, was seine Vielseitigkeit unter Beweis stellt.
Lineare Programmierung – FAQs
Was ist lineare Programmierung?
Lineare Programmierung ist ein mathematisches Konzept, das zur Optimierung eines bestimmten linearen Problems mit verschiedenen Einschränkungen verwendet wird. Mithilfe der linearen Programmierung ermitteln wir die optimale Ausgabe des gegebenen Problems
Was sind lineare Programmierprobleme?
Lineare Programmierprobleme (LPP) sind die Probleme, die die optimale Lösung für gegebene Bedingungen liefern.
Was ist eine lineare Programmierformel?
Allgemeine lineare Programmierformeln sind:
- Zielfunktion: Z = ax + by
- Einschränkungen: px + qy ≤ r, sx + ty ≤ u
- Nicht-negative Einschränkungen: x ≥ 0, y ≥ 0
Welche verschiedenen Arten der linearen Programmierung gibt es?
Verschiedene Arten linearer Programmiermethoden sind:
- Lineare Programmierung durch Simplex-Methode
- Lineare Programmierung mit der R-Methode
- Lineare Programmierung durch grafische Methode
Was sind Anforderungen der linearen Programmierung?
Verschiedene Anforderungen an lineare Programmierprobleme sind:
- Linearität
- Zielfunktion
- Einschränkungen
- Nicht-Negativität
Was sind die Vorteile der linearen Programmierung?
Verschiedene Vorteile der linearen Programmierung sind:
- Es bietet die optimale Lösung für jedes gegebene lineare Problem.
- Es ist einfach zu bedienen und liefert stets konsistente Ergebnisse
- Es hilft, den Gewinn zu maximieren und die Inputkosten zu senken.