Die logistische Regression in der R-Programmierung ist ein Klassifizierungsalgorithmus, der verwendet wird, um die Wahrscheinlichkeit für den Erfolg und Misserfolg eines Ereignisses zu ermitteln. Die logistische Regression wird verwendet, wenn die abhängige Variable binärer Natur ist (0/1, Wahr/Falsch, Ja/Nein). Die Logit-Funktion wird als Verknüpfungsfunktion in einer Binomialverteilung verwendet.
Die Wahrscheinlichkeit einer binären Ergebnisvariablen kann mithilfe der statistischen Modellierungstechnik, der sogenannten logistischen Regression, vorhergesagt werden. Es wird häufig in vielen verschiedenen Branchen eingesetzt, darunter Marketing, Finanzen, Sozialwissenschaften und medizinische Forschung.
Die logistische Funktion, allgemein als Sigmoidfunktion bezeichnet, ist die Grundidee, die der logistischen Regression zugrunde liegt. Diese Sigmoidfunktion wird in der logistischen Regression verwendet, um die Korrelation zwischen den Prädiktorvariablen und der Wahrscheinlichkeit des binären Ergebnisses zu beschreiben.

Logistische Regression in der R-Programmierung
Logistische Regression wird auch als bezeichnet Binomiale logistische Regression . Es basiert auf der Sigmoidfunktion, bei der die Ausgabe die Wahrscheinlichkeit ist und die Eingabe von -unendlich bis +unendlich reichen kann.
Theorie
Die logistische Regression wird auch als verallgemeinertes lineares Modell bezeichnet. Da es als Klassifizierungstechnik zur Vorhersage einer qualitativen Reaktion verwendet wird, liegt der Wert von y im Bereich von 0 bis 1 und kann durch die folgende Gleichung dargestellt werden:

Logistische Regression in der R-Programmierung
P ist die Wahrscheinlichkeit des interessierenden Merkmals. Das Odds Ratio ist definiert als die Erfolgswahrscheinlichkeit im Vergleich zur Misserfolgswahrscheinlichkeit. Es ist eine Schlüsseldarstellung logistischer Regressionskoeffizienten und kann Werte zwischen 0 und unendlich annehmen. Das Odds Ratio beträgt 1, wenn die Erfolgswahrscheinlichkeit gleich der Misserfolgswahrscheinlichkeit ist. Das Odds Ratio beträgt 2, wenn die Erfolgswahrscheinlichkeit doppelt so hoch ist wie die Misserfolgswahrscheinlichkeit. Das Odds Ratio beträgt 0,5, wenn die Wahrscheinlichkeit eines Scheiterns doppelt so hoch ist wie die Erfolgswahrscheinlichkeit.
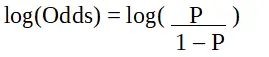
Logistische Regression in der R-Programmierung
Da wir mit einer Binomialverteilung (abhängige Variable) arbeiten, müssen wir eine Verknüpfungsfunktion auswählen, die für diese Verteilung am besten geeignet ist.
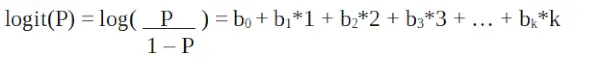
Logistische Regression in der R-Programmierung
es ist ein Logit-Funktion . In der obigen Gleichung wird die Klammer gewählt, um die Wahrscheinlichkeit der Beobachtung der Stichprobenwerte zu maximieren, anstatt die Summe der quadratischen Fehler zu minimieren (wie bei einer gewöhnlichen Regression). Das Logit wird auch als Quotenprotokoll bezeichnet. Die Logit-Funktion muss linear mit den unabhängigen Variablen verknüpft sein. Dies ergibt sich aus Gleichung A, wobei die linke Seite eine Linearkombination von x ist. Dies ähnelt der OLS-Annahme, dass y linear mit x zusammenhängt. Die Variablen b0, b1, b2 usw. sind unbekannt und müssen anhand verfügbarer Trainingsdaten geschätzt werden. In einem logistischen Regressionsmodell ändert die Multiplikation von b1 mit einer Einheit den Logit um b0. Die P-Änderungen aufgrund einer Änderung um eine Einheit hängen vom multiplizierten Wert ab. Wenn b1 positiv ist, nimmt P zu, und wenn b1 negativ ist, nimmt P ab.
Der Datensatz
mtcars (Motor Trend Car Road Test) umfasst Kraftstoffverbrauch, Leistung und 10 Aspekte des Automobildesigns für 32 Autos. Es ist vorinstalliert mit dplyr Paket in R.
R
Java-Sammlungen Java
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
>
Durchführen einer logistischen Regression für einen Datensatz
Die logistische Regression wird in R implementiert glm() durch Training des Modells mithilfe von Merkmalen oder Variablen im Datensatz.
R
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Aufteilen der Daten
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Ausgabe:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 1,58781 2,60087 0,610 0,5415 wt 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,882 0,0598 . --- Signif. Codes: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Dispersionsparameter für die Binomialfamilie wird mit 1 angenommen) Nullabweichung: 34,617 bei 24 Freiheitsgraden Restabweichung: 20,212 bei 22 Freiheitsgrade AIC: 26.212 Anzahl der Fisher-Scoring-Iterationen: 6>
- Aufruf: Der zur Anpassung des logistischen Regressionsmodells verwendete Funktionsaufruf wird zusammen mit Informationen zu Familie, Formel und Daten angezeigt. Abweichungsreste: Dies sind die Abweichungsreste, die den Grad der Anpassungsgüte des Modells messen. Sie stehen für Diskrepanzen zwischen tatsächlichen Antworten und der vom logistischen Regressionsmodell vorhergesagten Wahrscheinlichkeit. Koeffizienten: Diese Koeffizienten in der logistischen Regression stellen die Log-Odds oder den Logit der Antwortvariablen dar. Die Standardfehler im Zusammenhang mit den geschätzten Koeffizienten werden im Std. angezeigt. Fehlerspalte. Signifikanzcodes: Das Signifikanzniveau jeder Prädiktorvariablen wird durch die Signifikanzcodes angegeben. Dispersionsparameter: Bei der logistischen Regression dient der Dispersionsparameter als Skalierungsparameter für die Binomialverteilung. In diesem Fall ist es auf 1 gesetzt, was bedeutet, dass die angenommene Streuung 1 ist. Nullabweichung: Die Nullabweichung berechnet die Abweichung des Modells, wenn nur der Achsenabschnitt berücksichtigt wird. Es symbolisiert die Abweichung, die sich aus einem Modell ohne Prädiktoren ergeben würde. Restabweichung: Die Restabweichung berechnet die Abweichung des Modells nach der Anpassung der Prädiktoren. Sie steht für die Restabweichung nach Berücksichtigung der Prädiktoren. AIC: Das Akaike Information Criterion (AIC), das die Anzahl der Prädiktoren berücksichtigt, ist ein Maß für die Anpassungsgüte eines Modells. Kompliziertere Modelle werden bestraft, um eine Überanpassung zu verhindern. Besser passende Modelle werden durch niedrigere AIC-Werte angezeigt. Anzahl der Fisher-Scoring-Iterationen: Die Anzahl der Iterationen, die das Fisher-Scoring-Verfahren zur Schätzung der Modellparameter benötigt, wird durch die Anzahl der Iterationen angegeben.
Testdaten basierend auf dem Modell vorhersagen
R
Java analysiert String in int
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Ausgabe:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Ausgabe:
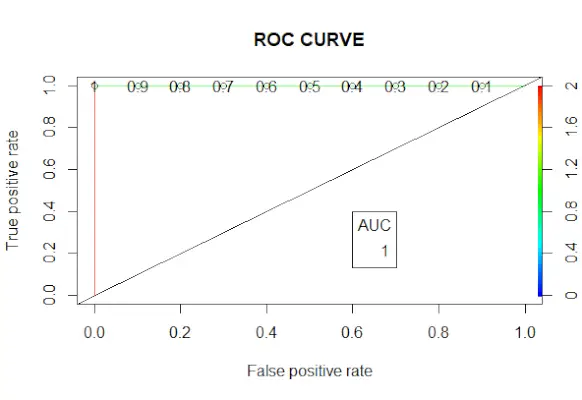
ROC-Kurve
Beispiel 2:
Wir können ein logistisches Regressionsmodell des Titanic-Datensatzes in R durchführen.
R
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Ausgabe:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 4.022e-16 8.660e-01 0 1 Class2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.551e-16 1.000e+ 00 0 1 SexFemale -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (Dispersionsparameter für Binomialfamilie wird mit 1 angenommen) Nullabweichung: 44.361 bei 31 Freiheitsgraden Restabweichung: 44.361 auf 26 Freiheitsgraden AIC: 56.361 Anzahl der Fisher-Scoring-Iterationen: 2>
Zeichnen Sie die ROC-Kurve für den Titanic-Datensatz
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
>
>
Ausgabe:
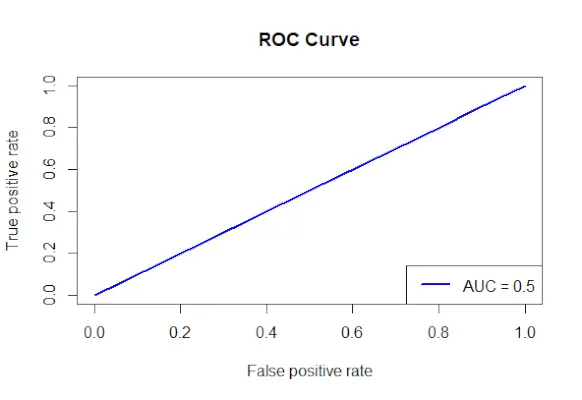
ROC-Kurve
- Die zur Vorhersage der Überlebensrate verwendeten Faktoren werden angegeben und die Formel „Überlebensklasse + Geschlecht + Alter“ wird verwendet, um ein logistisches Regressionsmodell zu erstellen.
- Mithilfe der Funktion „predict()“ werden anhand des angepassten Modells Vorhersagen für den Datensatz getroffen.
- Die projizierten Wahrscheinlichkeiten werden mit den tatsächlichen Ergebniswerten kombiniert, um mithilfe der Prediction()-Methode aus dem ROCR-Paket ein Vorhersageobjekt zu erstellen.
- Das Maß für die True-Positive-Rate (tpr) und das X-Achsen-Maß für die False-Positive-Rate (fpr) werden angegeben, und mithilfe der Funktion performance() aus dem ROCR-Paket wird ein ROC-Kurvenobjekt erstellt.
- Das ROC-Kurvenobjekt (roc_obj), das den Haupttitel, die Farbe und die Linienbreite angibt, wird mit der Funktion plot() geplottet.
- Es verwendet die Funktion performance() mit Measure = auc, um den AUC-Wert (Fläche unter der Kurve) zu bestimmen, und fügt dem Diagramm Beschriftungen und eine Legende hinzu.
