Was ist der niedrigste gemeinsame Vorfahre im Binärbaum?
Der niedrigster gemeinsamer Vorfahre ist der niedrigste Knoten im Baum, der sowohl n1 als auch n2 hat Nachkommenschaft, Dabei sind n1 und n2 die Knoten, für die wir die Ökobilanz ermitteln möchten. Daher ist die LCA eines Binärbaums mit den Knoten n1 und n2 der gemeinsame Vorfahre von n1 und n2, der am weitesten von der Wurzel entfernt ist.
Anwendung des niedrigsten gemeinsamen Vorfahren (LCA):
Um den Abstand zwischen Knotenpaaren in einem Baum zu bestimmen: Der Abstand von n1 zu n2 kann als Abstand von der Wurzel zu n1 plus dem Abstand von der Wurzel zu n2 minus dem doppelten Abstand von der Wurzel zu ihrem niedrigsten gemeinsamen Knoten berechnet werden Vorfahr.
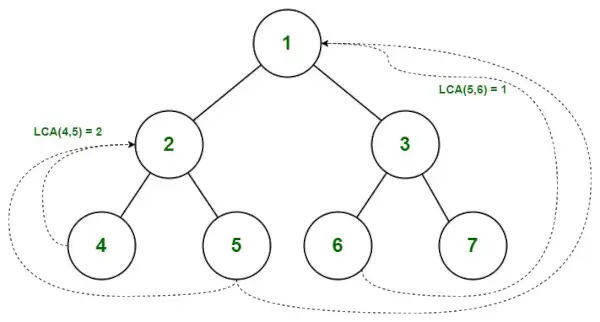
Niedrigster gemeinsamer Vorfahr im Binärbaum
Empfohlene Übung zum niedrigsten gemeinsamen Vorfahren in einem Binärbaum Probieren Sie es aus!
Niedrigster gemeinsamer Vorfahre in einem Binärbaum durch Speichern der Pfade von Wurzel zu n1 und Wurzel zu n2:
Die Idee dieses Ansatzes besteht darin, den Pfad von der Wurzel zu n1 und von der Wurzel zu n2 in zwei separaten Datenstrukturen zu speichern. Schauen Sie sich dann gleichzeitig die in der Datenstruktur gespeicherten Werte an und suchen Sie nach der ersten Nichtübereinstimmung.
Illustration:
Finden Sie die Ökobilanz von 5 und 6
Pfad von der Wurzel nach 5 = { 1, 2, 5 }
Pfad von Wurzel zu 6 = { 1, 3, 6 }
- Wir beginnen mit der Überprüfung ab Index 0. Da beide Werte übereinstimmen (pathA[0] = pathB[0]), gehen wir zum nächsten Index über.
- Wenn PfadA[1] nicht mit PfadB[1] übereinstimmt, liegt eine Nichtübereinstimmung vor, sodass wir den vorherigen Wert berücksichtigen.
- Daher ist die Ökobilanz von (5,6) = 1
Führen Sie die folgenden Schritte aus, um das Problem zu lösen:
- Finden Sie einen Pfad von der Wurzel zu n1 und speichern Sie ihn in einem Vektor oder Array.
- Finden Sie einen Pfad von der Wurzel zu n2 und speichern Sie ihn in einem anderen Vektor oder Array.
- Durchlaufen Sie beide Pfade, bis die Werte in den Arrays gleich sind. Gibt das gemeinsame Element direkt vor der Nichtübereinstimmung zurück.
Es folgt die Implementierung des obigen Algorithmus:
C++
// C++ Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> #include> using> namespace> std;> // A Binary Tree node> struct> Node {> >int> key;> >struct> Node *left, *right;> };> // Utility function creates a new binary tree node with> // given key> Node* newNode(>int> k)> {> >Node* temp =>new> Node;> >temp->key = k;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // Finds the path from root node to given root of the tree,> // Stores the path in a vector path[], returns true if path> // exists otherwise false> bool> findPath(Node* root, vector<>int>>& Pfad,>int> k)> (root->right && findPath(root->right, path, k)))> >return> true>;> >// If not present in subtree rooted with root, remove> >// root from path[] and return false> >path.pop_back();> >return> false>;> > // Returns LCA if node n1, n2 are present in the given> // binary tree, otherwise return -1> int> findLCA(Node* root,>int> n1,>int> n2)> > // Driver program to test above functions> int> main()> {> >// Let us create the Binary Tree shown in above diagram.> >Node* root = newNode(1);> >root->left = newNode(2);> >root->right = newNode(3);> >root->left->left = newNode(4);> >root->links->rechts = newNode(5);> >root->rechts->links = newNode(6);> >root->right->right = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5);> >cout <<>'
LCA(4, 6) = '> << findLCA(root, 4, 6);> >cout <<>'
LCA(3, 4) = '> << findLCA(root, 3, 4);> >cout <<>'
LCA(2, 4) = '> << findLCA(root, 2, 4);> >return> 0;> }> |
>
>
Java
// Java Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA of> // two given values n1 and n2> import> java.util.ArrayList;> import> java.util.List;> // A Binary Tree node> class> Node {> >int> data;> >Node left, right;> >Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> List path1 =>new> ArrayList();> >private> List path2 =>new> ArrayList();> >// Finds the path from root node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.clear();> >path2.clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >System.out.println((path1.size()>>0>)> >?>'n1 is present'> >:>'n1 is missing'>);> >System.out.println((path2.size()>>0>)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> ->1>;> >}> >int> i;> >for> (i =>0>; i i++) { // System.out.println(path1.get(i) + ' ' + // path2.get(i)); if (!path1.get(i).equals(path2.get(i))) break; } return path1.get(i - 1); } // Finds the path from root node to given root of the // tree, Stores the path in a vector path[], returns // true if path exists otherwise false private boolean findPath(Node root, int n, List path) { // base case if (root == null) { return false; } // Store this node . The node will be removed if // not in path from root to n. path.add(root.data); if (root.data == n || findPath(root.left, n, path) || findPath(root.right, n, path)) { return true; } // If not present in subtree rooted with root, // remove root from path[] and return false path.remove(path.size() - 1); return false; } // Driver code public static void main(String[] args) { BT_NoParentPtr_Solution1 tree = new BT_NoParentPtr_Solution1(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); tree.root.right.left = new Node(6); tree.root.right.right = new Node(7); System.out.println('LCA(4, 5) = ' + tree.findLCA(4, 5)); System.out.println('LCA(4, 6) = ' + tree.findLCA(4, 6)); System.out.println('LCA(3, 4) = ' + tree.findLCA(3, 4)); System.out.println('LCA(2, 4) = ' + tree.findLCA(2, 4)); } } // This code is contributed by Sreenivasulu Rayanki.> |
>
>
Python3
# Python Program for Lowest Common Ancestor in a Binary Tree> # O(n) solution to find LCS of two given values n1 and n2> # A binary tree node> class> Node:> ># Constructor to create a new binary node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # Finds the path from root node to given root of the tree.> # Stores the path in a list path[], returns true if path> # exists otherwise false> def> findPath(root, path, k):> ># Baes Case> >if> root>is> None>:> >return> False> ># Store this node is path vector. The node will be> ># removed if not in path from root to k> >path.append(root.key)> ># See if the k is same as root's key> >if> root.key>=>=> k:> >return> True> ># Check if k is found in left or right sub-tree> >if> ((root.left !>=> None> and> findPath(root.left, path, k))>or> >(root.right !>=> None> and> findPath(root.right, path, k))):> >return> True> ># If not present in subtree rooted with root, remove> ># root from path and return False> >path.pop()> >return> False> # Returns LCA if node n1 , n2 are present in the given> # binary tree otherwise return -1> def> findLCA(root, n1, n2):> ># To store paths to n1 and n2 fromthe root> >path1>=> []> >path2>=> []> ># Find paths from root to n1 and root to n2.> ># If either n1 or n2 is not present , return -1> >if> (>not> findPath(root, path1, n1)>or> not> findPath(root, path2, n2)):> >return> ->1> ># Compare the paths to get the first different value> >i>=> 0> >while>(i <>len>(path1)>and> i <>len>(path2)):> >if> path1[i] !>=> path2[i]:> >break> >i>+>=> 1> >return> path1[i>->1>]> # Driver program to test above function> if> __name__>=>=> '__main__'>:> > ># Let's create the Binary Tree shown in above diagram> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> > >print>(>'LCA(4, 5) = %d'> %> (findLCA(root,>4>,>5>,)))> >print>(>'LCA(4, 6) = %d'> %> (findLCA(root,>4>,>6>)))> >print>(>'LCA(3, 4) = %d'> %> (findLCA(root,>3>,>4>)))> >print>(>'LCA(2, 4) = %d'> %> (findLCA(root,>2>,>4>)))> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
// C# Program for Lowest Common> // Ancestor in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> using> System.Collections;> using> System;> // A Binary Tree node> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> ArrayList path1 =>new> ArrayList();> >private> ArrayList path2 =>new> ArrayList();> >// Finds the path from root> >// node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.Clear();> >path2.Clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >Console.Write((path1.Count>0)> >?>'n1 is present'> >:>'n1 is missing'>);> >Console.Write((path2.Count>0)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> -1;> >}> >int> i;> >for> (i = 0; i i++) { // System.out.println(path1.get(i) // + ' ' + path2.get(i)); if ((int)path1[i] != (int)path2[i]) break; } return (int)path1[i - 1]; } // Finds the path from root node // to given root of the tree, // Stores the path in a vector // path[], returns true if path // exists otherwise false private bool findPath(Node root, int n, ArrayList path) { // base case if (root == null) { return false; } // Store this node . The node // will be removed if not in // path from root to n. path.Add(root.data); if (root.data == n) { return true; } if (root.left != null && findPath(root.left, n, path)) { return true; } if (root.right != null && findPath(root.right, n, path)) { return true; } // If not present in subtree // rooted with root, remove root // from path[] and return false path.RemoveAt(path.Count - 1); return false; } // Driver code public static void Main(String[] args) { BT_NoParentPtr_Solution1 tree = new BT_NoParentPtr_Solution1(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); tree.root.right.left = new Node(6); tree.root.right.right = new Node(7); Console.Write('LCA(4, 5) = ' + tree.findLCA(4, 5)); Console.Write('
LCA(4, 6) = ' + tree.findLCA(4, 6)); Console.Write('
LCA(3, 4) = ' + tree.findLCA(3, 4)); Console.Write('
LCA(2, 4) = ' + tree.findLCA(2, 4)); } } // This code is contributed by Rutvik_56> |
>
>
Javascript
> >// JavaScript Program for Lowest Common> >// Ancestor in a Binary Tree> >// A O(n) solution to find LCA of> >// two given values n1 and n2> > >class Node> >{> >constructor(value) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = value;> >}> >}> > >let root;> >let path1 = [];> >let path2 = [];> > >// Finds the path from root node to given root of the tree.> >function> findLCA(n1, n2) {> >path1 = [];> >path2 = [];> >return> findLCAInternal(root, n1, n2);> >}> > >function> findLCAInternal(root, n1, n2) {> > >if> (!findPath(root, n1, path1) || !findPath(root, n2, path2))> >{> >document.write((path1.length>0) ?> >'n1 is present'> :>'n1 is missing'>);> >document.write((path2.length>0) ?> >'n2 is present'> :>'n2 is missing'>);> >return> -1;> >}> > >let i;> >for> (i = 0; i // System.out.println(path1.get(i) + ' ' + path2.get(i)); if (path1[i] != path2[i]) break; } return path1[i-1]; } // Finds the path from root node to // given root of the tree, Stores the // path in a vector path[], returns true // if path exists otherwise false function findPath(root, n, path) { // base case if (root == null) { return false; } // Store this node . The node will be removed if // not in path from root to n. path.push(root.data); if (root.data == n) { return true; } if (root.left != null && findPath(root.left, n, path)) { return true; } if (root.right != null && findPath(root.right, n, path)) { return true; } // If not present in subtree rooted with root, // remove root from // path[] and return false path.pop(); return false; } root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7); document.write('LCA(4, 5) = ' + findLCA(4,5) + ''); document.write('LCA(4, 6) = ' + findLCA(4,6) + ''); document.write('LCA(3, 4) = ' + findLCA(3,4) + ''); document.write('LCA(2, 4) = ' + findLCA(2,4));> |
>
>Ausgabe
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>
Zeitkomplexität: AN). Der Baum wird zweimal durchlaufen und dann werden die Pfadarrays verglichen.
Hilfsraum: AN). Zusätzlicher Platz für Pfad1 und Pfad2.
Niedrigster gemeinsamer Vorfahre in einem Binärbaum durch einzelne Durchquerung:
Die Idee besteht darin, den Baum ausgehend von der Wurzel zu durchqueren. Wenn einer der angegebenen Schlüssel (n1 und n2) mit der Wurzel übereinstimmt, dann ist die Wurzel LCA (vorausgesetzt, dass beide Schlüssel vorhanden sind). Wenn die Wurzel mit keinem der Schlüssel übereinstimmt, wiederholen wir den Vorgang für den linken und rechten Teilbaum.
- Der Knoten, bei dem ein Schlüssel im linken Teilbaum und der andere Schlüssel im rechten Teilbaum vorhanden ist, ist der LCA.
- Wenn beide Schlüssel im linken Teilbaum liegen, dann hat der linke Teilbaum auch LCA,
- Andernfalls liegt LCA im rechten Teilbaum.
Illustration:
Finden Sie die Ökobilanz von 5 und 6
Wurzel zeigt auf den Knoten mit dem Wert 1, da sein Wert nicht mit { 5, 6 } übereinstimmt. Wir suchen den Schlüssel im linken Teilbaum und im rechten Teilbaum.
- Linker Teilbaum:
- Neue Wurzel = { 2 } ≠ 5 oder 6, daher werden wir unsere Rekursion fortsetzen
- New Root = { 4 } , der linke und rechte Teilbaum sind null, wir geben für diesen Aufruf NULL zurück
- Neuer Stamm = { 5 } , der Wert stimmt mit 5 überein und gibt daher den Knoten mit dem Wert 5 zurück
- Der Funktionsaufruf für root mit dem Wert 2 gibt einen Wert von 5 zurück
- Rechter Teilbaum:
- Wurzel = { 3 } ≠ 5 oder 6 daher setzen wir unsere Rekursion fort
- Root = { 6 } = 5 oder 6 , wir geben diesen Knoten mit dem Wert 6 zurück
- Root = { 7 } ≠ 5 oder 6, wir geben NULL zurück
- Der Funktionsaufruf für root mit dem Wert 3 gibt also einen Knoten mit dem Wert 6 zurück
- Da sowohl der linke als auch der rechte Teilbaum des Knotens mit dem Wert 1 nicht NULL sind, ist 1 die Ökobilanz
Führen Sie die folgenden Schritte aus, um das Problem zu lösen:
- Wir übergeben die Wurzel an eine Hilfsfunktion und prüfen, ob der Wert der Wurzel mit einem von n1 und n2 übereinstimmt.
- Wenn JA, geben Sie den Stamm zurück
- sonst rekursiver Aufruf im linken und rechten Teilbaum
- Grundsätzlich führen wir eine Vorbestellungsdurchquerung durch. Zuerst prüfen wir, ob der Root->Wert mit n1 oder n2 übereinstimmt. Dann durchqueren Sie den linken und rechten Teilbaum.
- Wenn es eine Wurzel gibt, die einen NULL- und einen anderen NON-NULL-Wert zurückgibt, werden wir den entsprechenden NON-NULL-Wert für diesen Knoten zurückgeben.
- Der Knoten, der sowohl für den linken als auch für den rechten Teilbaum beide NON-NULL-Werte zurückgibt, ist unser niedrigster gemeinsamer Vorfahre.
Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes.
C++
/* C++ Program to find LCA of n1 and n2 using one traversal> >* of Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->key = key;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> struct> Node* findLCA(>struct> Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->Schlüssel == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->left = newNode(2);> >root->right = newNode(3);> >root->left->left = newNode(4);> >root->links->rechts = newNode(5);> >root->rechts->links = newNode(6);> >root->right->right = newNode(7);> >cout <<>'LCA(4, 5) = '> cout << '
LCA(4, 6) = ' cout << '
LCA(3, 4) = ' cout << '
LCA(2, 4) = ' return 0; } // This code is contributed by Aditya Kumar (adityakumar129)> |
>
>
C
// C Program to find LCA of n1 and n2 using one traversalof> // Binary Tree> #include> #include> // A Binary Tree Node> typedef> struct> Node {> >struct> Node *left, *right;> >int> key;> } Node;> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp = (Node*)>malloc>(>sizeof>(Node));> >temp->key = key;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> Node* findLCA(Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->Schlüssel == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->left = newNode(2);> >root->right = newNode(3);> >root->left->left = newNode(4);> >root->links->rechts = newNode(5);> >root->rechts->links = newNode(6);> >root->right->right = newNode(7);> >printf>(>'LCA(4, 5) = %d'>, findLCA(root, 4, 5)->Schlüssel);> >printf>(>'
LCA(4, 6) = %d'>, findLCA(root, 4, 6)->Schlüssel);> >printf>(>'
LCA(3, 4) = %d'>, findLCA(root, 3, 4)->Schlüssel);> >printf>(>'
LCA(2, 4) = %d'>, findLCA(root, 2, 4)->Schlüssel);> >return> 0;> }> // This code is contributed by Aditya Kumar (adityakumar129)> |
>
>
Java
// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> /* Class containing left and right child of current> >node and key value*/> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> >> >// Base case> >if> (node ==>null>)> >return> null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by returning root (Note that> >// if a key is ancestor of other, then the ancestor> >// key becomes LCA> >if> (node.data == n1> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ tree.findLCA(>4>,>5>).data);> >System.out.println(>'LCA(4, 6) = '> >+ tree.findLCA(>4>,>6>).data);> >System.out.println(>'LCA(3, 4) = '> >+ tree.findLCA(>3>,>4>).data);> >System.out.println(>'LCA(2, 4) = '> >+ tree.findLCA(>2>,>4>).data);> >}> }> |
>
>
Python3
# Python program to find LCA of n1 and n2 using one> # traversal of Binary tree> # A binary tree node> class> Node:> ># Constructor to create a new tree node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function returns pointer to LCA of two given> # values n1 and n2> # This function assumes that n1 and n2 are present in> # Binary Tree> def> findLCA(root, n1, n2):> ># Base Case> >if> root>is> None>:> >return> None> ># If either n1 or n2 matches with root's key, report> ># the presence by returning root (Note that if a key is> ># ancestor of other, then the ancestor key becomes LCA> >if> root.key>=>=> n1>or> root.key>=>=> n2:> >return> root> ># Look for keys in left and right subtrees> >left_lca>=> findLCA(root.left, n1, n2)> >right_lca>=> findLCA(root.right, n1, n2)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> # Driver code> if> __name__>=>=> '__main__'>:> > ># Let us create a binary tree given in the above example> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>).key)> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>).key)> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>).key)> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>).key)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
// C# implementation to find lowest common> // ancestor of n1 and n2 using one traversal> // of binary tree> using> System;> // Class containing left and right> // child of current node and key value> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA> >// of two given values n1 and n2. This> >// function assumes that n1 and n2 are> >// present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> > node.data == n2)> >return> node;> >// Look for keys in left and right subtrees> >Node left_lca = findLCA(node.left, n1, n2);> >Node right_lca = findLCA(node.right, n1, n2);> >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree> >// and other is present in other, So this> >// node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or> >// right subtree is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >> >// Driver code> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> >+ tree.findLCA(4, 5).data);> >Console.WriteLine(>'LCA(4, 6) = '> >+ tree.findLCA(4, 6).data);> >Console.WriteLine(>'LCA(3, 4) = '> >+ tree.findLCA(3, 4).data);> >Console.WriteLine(>'LCA(2, 4) = '> >+ tree.findLCA(2, 4).data);> >}> }> // This code is contributed by pratham76> |
>
>
Javascript
> >// JavaScript implementation to find> >// lowest common ancestor of> >// n1 and n2 using one traversal of binary tree> > >class Node> >{> >constructor(item) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = item;> >}> >}> > >//Root of the Binary Tree> >let root;> > >function> findlCA(n1, n2)> >{> >return> findLCA(root, n1, n2);> >}> > >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >function> findLCA(node, n1, n2)> >> > >root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >document.write(>'LCA(4, 5) = '> +> >findlCA(4, 5).data +>''>);> >document.write(>'LCA(4, 6) = '> +> >findlCA(4, 6).data +>''>);> >document.write(>'LCA(3, 4) = '> +> >findlCA(3, 4).data +>''>);> >document.write(>'LCA(2, 4) = '> +> >findlCA(2, 4).data +>''>);> > > |
>
>Ausgabe
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>
Zeitkomplexität : O(N), da die Methode eine einfache Baumdurchquerung von unten nach oben durchführt.
Hilfsraum: O(H), wobei H die Höhe des Baumes ist.
Notiz: Die obige Methode geht davon aus Schlüssel sind im Binärbaum vorhanden . Wenn ein Schlüssel vorhanden ist und der andere nicht, wird der aktuelle Schlüssel als LCA zurückgegeben (idealerweise sollte NULL zurückgegeben werden). Wir können diese Methode auf alle Fälle erweitern, indem wir zuerst prüfen, ob n1 und n2 im Baum vorhanden sind, und dann die Ökobilanz von n1 und n2 ermitteln. Um zu überprüfen, ob der Knoten im Binärbaum vorhanden ist oder nicht, durchlaufen Sie den Baum für die Knoten n1 und n2 getrennt.
C++
/* C++ program to find LCA of n1 and n2 using one traversal> >of Binary Tree. It handles all cases even when n1 or n2> >is not there in Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->key = key;> >temp->links = temp->rechts = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given> // valuesn1 and n2.> struct> Node* findLCAUtil(>struct> Node* root,>int> n1,>int> n2)> > // Returns true if key k is present in tree rooted with root> bool> find(Node* root,>int> k)> find(root->richtig, k))> >return> true>;> >// Else return false> >return> false>;> > // This function returns LCA of n1 and n2 only if both n1> // and n2 are present in tree, otherwise returns NULL;> Node* findLCA(Node* root,>int> n1,>int> n2)> {> >// Return LCA only if both n1 and n2 are present in tree> >if> (find(root, n1) and find(root, n2))> >return> findLCAUtil(root, n1, n2);> >// Else return NULL> >return> NULL;> }> // Driver program to test above functions> int> main()> {> >// Let us create a binary tree given in the above> >// example> >Node* root = newNode(1);> >root->left = newNode(2);> >root->right = newNode(3);> >root->left->left = newNode(4);> >root->links->rechts = newNode(5);> >root->rechts->links = newNode(6);> >root->right->right = newNode(7);> >Node* lca = findLCA(root, 4, 5);> >if> (lca != NULL)> >cout <<>'LCA(4, 5) = '> else cout << 'Keys are not present '; lca = findLCA(root, 4, 10); if (lca != NULL) cout << '
LCA(4, 10) = ' else cout << '
Keys are not present '; return 0; } // This code is contributed by Kshitij Dwivedi // (kshitijdwivedi28)> |
>
>
Java
// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >static> boolean> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >Node findLCAUtil(Node node,>int> n1,>int> n2)> >{> >// Base case> >if> (node ==>null>)> >return> null>;> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>)> >return> temp;> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2)> >return> lca;> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >Node lca = tree.findLCA(>4>,>5>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 5) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >lca = tree.findLCA(>4>,>10>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 10) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >}> }> |
>
>
Python3
''' Program to find LCA of n1 and n2 using one traversal of> >Binary tree> It handles all cases even when n1 or n2 is not there in tree> '''> # A binary tree node> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function return pointer to LCA of two given values> # n1 and n2> # v1 is set as true by this function if n1 is found> # v2 is set as true by this function if n2 is found> def> findLCAUtil(root, n1, n2, v):> ># Base Case> >if> root>is> None>:> >return> None> ># IF either n1 or n2 matches ith root's key, report> ># the presence by setting v1 or v2 as true and return> ># root (Note that if a key is ancestor of other, then> ># the ancestor key becomes LCA)> >if> root.key>=>=> n1:> >v[>0>]>=> True> >return> root> >if> root.key>=>=> n2:> >v[>1>]>=> True> >return> root> ># Look for keys in left and right subtree> >left_lca>=> findLCAUtil(root.left, n1, n2, v)> >right_lca>=> findLCAUtil(root.right, n1, n2, v)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> def> find(root, k):> ># Base Case> >if> root>is> None>:> >return> False> ># If key is present at root, or if left subtree or right> ># subtree , return true> >if> (root.key>=>=> k>or> find(root.left, k)>or> >find(root.right, k)):> >return> True> ># Else return false> >return> False> # This function returns LCA of n1 and n2 on value if both> # n1 and n2 are present in tree, otherwise returns None> def> findLCA(root, n1, n2):> ># Initialize n1 and n2 as not visited> >v>=> [>False>,>False>]> ># Find lca of n1 and n2 using the technique discussed above> >lca>=> findLCAUtil(root, n1, n2, v)> ># Returns LCA only if both n1 and n2 are present in tree> >if> (v[>0>]>and> v[>1>]>or> v[>0>]>and> find(lca, n2)>or> v[>1>]>and> >find(lca, n1)):> >return> lca> ># Else return None> >return> None> # Driver program to test above function> root>=> Node(>1>)> root.left>=> Node(>2>)> root.right>=> Node(>3>)> root.left.left>=> Node(>4>)> root.left.right>=> Node(>5>)> root.right.left>=> Node(>6>)> root.right.right>=> Node(>7>)> lca>=> findLCA(root,>4>,>5>)> if> lca>is> not> None>:> >print>(>'LCA(4, 5) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> lca>=> findLCA(root,>4>,>10>)> if> lca>is> not> None>:> >print>(>'LCA(4,10) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
using> System;> // c# implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >public> Node root;> >public> static> bool> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >public> virtual> Node findLCAUtil(Node node,>int> n1,> >int> n2)> >{> >// Base case> >if> (node ==>null>) {> >return> null>;> >}> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>) {> >return> temp;> >}> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>) {> >return> node;> >}> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >public> virtual> Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2) {> >return> lca;> >}> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Node lca = tree.findLCA(4, 5);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 5) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >lca = tree.findLCA(4, 10);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 10) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >}> }> // This code is contributed by Shrikant13> |
>
>
Javascript
> // JavaScript implementation to find lowest> // common ancestor of n1 and n2 using one> // traversal of binary tree. It also handles> // cases even when n1 and n2 are not there in Tree> // Class containing left and right child> // of current node and key> class Node> {> >constructor(item)> >{> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> class BinaryTree{> > // Root of the Binary Tree> constructor()> {> >this>.root =>null>;> >this>.v1 =>false>;> >this>.v2 =>false>;> }> // This function returns pointer to LCA> // of two given values n1 and n2.> // v1 is set as true by this function> // if n1 is found> // v2 is set as true by this function> // if n2 is found> findLCAUtil(node, n1, n2)> {> > >// Base case> >if> (node ==>null>)> >{> >return> null>;> >}> > >// Store result in temp, in case of> >// key match so that we can search> >// for other key also.> >var> temp =>null>;> > >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as> >// true and return root (Note that if a key> >// is ancestor of other, then the ancestor> >// key becomes LCA)> >if> (node.data == n1)> >{> >this>.v1 =>true>;> >temp = node;> >}> >if> (node.data == n2)> >{> >this>.v2 =>true>;> >temp = node;> >}> > >// Look for keys in left and right subtrees> >var> left_lca =>this>.findLCAUtil(node.left, n1, n2);> >var> right_lca =>this>.findLCAUtil(node.right, n1, n2);> > >if> (temp !=>null>)> >{> >return> temp;> >}> > >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree and> >// other is present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >{> >return> node;> >}> > >// Otherwise check if left subtree or> >// right subtree is LCA> >return> left_lca !=>null> ? left_lca : right_lca;> }> // Finds lca of n1 and n2 under the> // subtree rooted with 'node'> findLCA(n1, n2)> {> > >// Initialize n1 and n2 as not visited> >this>.v1 =>false>;> >this>.v2 =>false>;> > >// Find lca of n1 and n2 using the> >// technique discussed above> >var> lca =>this>.findLCAUtil(>this>.root, n1, n2);> > >// Return LCA only if both n1 and n2> >// are present in tree> >if> (>this>.v1 &&>this>.v2)> >{> >return> lca;> >}> > >// Else return NULL> >return> null>;> }> }> // Driver code> var> tree =>new> BinaryTree();> tree.root =>new> Node(1);> tree.root.left =>new> Node(2);> tree.root.right =>new> Node(3);> tree.root.left.left =>new> Node(4);> tree.root.left.right =>new> Node(5);> tree.root.right.left =>new> Node(6);> tree.root.right.right =>new> Node(7);> var> lca = tree.findLCA(4, 5);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 5) = '> +> >lca.data +>' '>);> }>else> {> >document.write(>'Keys are not present'> +>' '>);> }> lca = tree.findLCA(4, 10);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 10) = '> +> >lca.data +>' '>);> }> else> {> >document.write(>'Keys are not present'> +>' '>);> }> // This code is contributed by rdtank> > |
>
>Ausgabe
LCA(4, 5) = 2 Keys are not present>
Zeitkomplexität : O(N), da die Methode eine einfache Baumdurchquerung von unten nach oben durchführt.
Hilfsraum: O(H), wobei h die Höhe des Baumes ist.
Verwendung einer Hilfsdatenstruktur (Hash-Tabelle):
The basic idea behind the 'Using an auxiliary data structure' approach for finding the lowest common ancestor of two nodes in a binary tree is to use a hash table or a map to store the parent pointers of each node. Once we have the parent pointers, we can traverse up from the first node and add all its ancestors to a set or a list. Then we can traverse up from the second node and check if each ancestor is already in the set or the list. The first ancestor that is already in the set or the list is the lowest common ancestor.>
Befolgen Sie die Schritte, um den oben genannten Ansatz umzusetzen:
- Erstellen Sie eine Hash-Tabelle oder eine Karte, um die übergeordneten Zeiger jedes Knotens im Binärbaum zu speichern.
- Durchlaufen Sie den Binärbaum und füllen Sie die Hash-Tabelle oder die Karte mit den übergeordneten Zeigern für jeden Knoten.
- Beginnen Sie mit dem ersten Knoten, durchlaufen Sie den Baum nach oben und fügen Sie jeden Vorfahren zu einer Menge oder einer Liste hinzu.
- Gehen Sie ausgehend vom zweiten Knoten den Baum nach oben und prüfen Sie, ob jeder Vorfahre bereits in der Menge oder Liste enthalten ist. Der erste Vorfahre, der bereits in der Menge oder der Liste vorhanden ist, ist der niedrigste gemeinsame Vorfahre.
- Wenn kein gemeinsamer Vorfahre gefunden wird, geben Sie null oder einen anderen Wert zurück, der das Fehlen eines gemeinsamen Vorfahren anzeigt.
Nachfolgend finden Sie die Implementierung für den oben genannten Ansatz:
C++
// C++ code to implement above approach> #include> #include> #include> #include> using> namespace> std;> // Definition of a binary tree node> struct> Node {> >int> data;> >Node* left;> >Node* right;> };> // Function to create a new binary tree node> Node* newNode(>int> data)> {> >Node* node =>new> Node;> >node->data = data;> >node->left = NULL;> >node->rechts = NULL;> >return> (node);> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> unordered_map buildParentMap(Node* root)> {> >unordered_map parentMap;> >parentMap[root] = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->links) {> >parentMap[node->left] = node;> >queue.push_back(node->links);> >}> >if> (node->rechts) {> >parentMap[node->rechts] = Knoten;> >queue.push_back(node->rechts);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two nodes> // using an auxiliary data structure> int> findLCA(Node* root,>int> n1,>int> n2)> {> >// Build a hash table or a map of parent pointers for> >// each node in the tree> >unordered_map parentMap> >= buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node* p = NULL;> >Node* q = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->Daten == n1) {> >p = node;> >}> >if> (node->Daten == n2) {> >q = node;> >}> >if> (node->links) {> >queue.push_back(node->links);> >}> >if> (node->rechts) {> >queue.push_back(node->rechts);> >}> >}> >// Add all the ancestors of the first node to a set or a> >// list> >set ancestors;> >while> (p) {> >ancestors.insert(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if each> >// ancestor is already in the set or the list> >while> (q) {> >if> (ancestors.find(q) != ancestors.end()) {> >return> q> >->Daten;>// The first ancestor that is> >// already in the set or the list is> >// the lowest common ancestor> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> }> // Driver code> int> main()> {> >Node* root = newNode(1);> >root->left = newNode(2);> >root->right = newNode(3);> >root->left->left = newNode(4);> >root->links->rechts = newNode(5);> >root->rechts->links = newNode(6);> >root->right->right = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5) << endl;> >cout <<>'LCA(4, 6) = '> << findLCA(root, 4, 6) << endl;> >cout <<>'LCA(3,4) = '> << findLCA(root, 3, 4) << endl;> >cout <<>'LCA(2, 4) = '> << findLCA(root, 2, 4) << endl;> >return> 0;> }> // This code is contributed by Veerendra_Singh_Rajpoot> |
>
>
Java
import> java.util.*;> // Definition of a binary tree node> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> Main {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Map buildParentMap(Node root)> >{> >Map parentMap =>new> HashMap();> >parentMap.put(root,>null>);> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.left !=>null>) {> >parentMap.put(node.left, node);> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.put(node.right, node);> >queue.add(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> findLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Map parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.data == n1) {> >p = node;> >}> >if> (node.data == n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >queue.add(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >Set ancestors =>new> HashSet();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.contains(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> ->1>;>// No common ancestor found> >}> >public> static> void> main(String[] args)> >{> >Node root =>new> Node(>1>);> >root.left =>new> Node(>2>);> >root.right =>new> Node(>3>);> >root.left.left =>new> Node(>4>);> >root.left.right =>new> Node(>5>);> >root.right.left =>new> Node(>6>);> >root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ findLCA(root,>4>,>5>));> >System.out.println(>'LCA(4, 6) = '> >+ findLCA(root,>4>,>6>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>3>,>4>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>2>,>4>));> >}> }> |
>
>
Python3
from> collections>import> deque> # Definition of a binary tree node> class> Node:> >def> __init__(>self>, data):> >self>.data>=> data> >self>.left>=> None> >self>.right>=> None> # Function to build a hash table or a map of parent> # pointers for each node in the tree> def> buildParentMap(root):> >parentMap>=> {}> >parentMap[root]>=> None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.left:> >parentMap[node.left]>=> node> >queue.append(node.left)> >if> node.right:> >parentMap[node.right]>=> node> >queue.append(node.right)> >return> parentMap> # Function to find the lowest common ancestor of two nodes> # using an auxiliary data structure> def> findLCA(root, n1, n2):> ># Build a hash table or a map of parent pointers for> ># each node in the tree> >parentMap>=> buildParentMap(root)> ># Find the nodes with values n1 and n2> >p, q>=> None>,>None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.data>=>=> n1:> >p>=> node> >if> node.data>=>=> n2:> >q>=> node> >if> node.left:> >queue.append(node.left)> >if> node.right:> >queue.append(node.right)> ># Add all the ancestors of the first node to a set or a> ># list> >ancestors>=> set>()> >while> p:> >ancestors.add(p)> >p>=> parentMap[p]> ># Traverse up from the second node and check if each> ># ancestor is already in the set or the list> >while> q:> >if> q>in> ancestors:> >return> q.data> >q>=> parentMap[q]> >return> ->1> # No common ancestor found> # Driver code> if> __name__>=>=> '__main__'>:> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>))> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>))> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>))> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>))> |
>
>
C#
using> System;> using> System.Collections.Generic;> // Definition of a binary tree node> class> Node> {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> MainClass> {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Dictionary BuildParentMap(Node root)> >{> >Dictionary parentMap =>new> Dictionary();> >parentMap.Add(root,>null>);> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.left !=>null>)> >{> >parentMap.Add(node.left, node);> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >parentMap.Add(node.right, node);> >queue.Enqueue(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> FindLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Dictionary parentMap = BuildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.data == n1)> >{> >p = node;> >}> >if> (node.data == n2)> >{> >q = node;> >}> >if> (node.left !=>null>)> >{> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >queue.Enqueue(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >HashSet ancestors =>new> HashSet();> >while> (p !=>null>)> >{> >ancestors.Add(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>)> >{> >if> (ancestors.Contains(q))> >{> >return> q.data;> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> >}> >public> static> void> Main()> >{> >Node root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> + FindLCA(root, 4, 5));> >Console.WriteLine(>'LCA(4, 6) = '> + FindLCA(root, 4, 6));> >Console.WriteLine(>'LCA(3, 4) = '> + FindLCA(root, 3, 4));> >Console.WriteLine(>'LCA(2, 4) = '> + FindLCA(root, 2, 4));> >}> }> // This code is contributed by akashish__> |
>
>
Javascript
// javascript code addition> // Definition of a binary tree node> class Node {> >constructor(item) {> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> function> buildParentMap(root) {> >const parentMap =>new> Map();> >parentMap.set(root,>null>);> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.left !=>null>) {> >parentMap.set(node.left, node);> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.set(node.right, node);> >queue.push(node.right);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two> // nodes using an auxiliary data structure> function> findLCA(root, n1, n2) {> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >const parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >let p =>null>, q =>null>;> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.data === n1) {> >p = node;> >}> >if> (node.data === n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >queue.push(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >const ancestors =>new> Set();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.has(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> -1;>// No common ancestor found> }> // Test the function> const root =>new> Node(1);> root.left =>new> Node(2);> root.right =>new> Node(3);> root.left.left =>new> Node(4);> root.left.right =>new> Node(5);> root.right.left =>new> Node(6);> root.right.right =>new> Node(7);> console.log(>'LCA(4, 5) = '> + findLCA(root, 4, 5));> console.log(>'LCA(4, 6) = '> + findLCA(root, 4, 6));> console.log(>'LCA(3, 4) = '> + findLCA(root, 3, 4));> console.log(>'LCA(2, 4) = '> + findLCA(root, 2, 4));> // The code is contributed by Nidhi goel.> |
>
>Ausgabe
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3,4) = 1 LCA(2, 4) = 2>
Zeitkomplexität: O(n),
Angular CLI deinstallieren
Die zeitliche Komplexität des gegebenen Codes beträgt O(n), wobei n die Anzahl der Knoten im Binärbaum ist.
Um die übergeordnete Karte für jeden Knoten im Baum zu erstellen, muss jeder Knoten einmal besucht werden, was O(n) Zeit in Anspruch nimmt. Um die Knoten mit den Werten n1 und n2 zu finden, muss jeder Knoten einmal besucht werden, was ebenfalls O(n) Zeit in Anspruch nimmt. Der Übergang vom zweiten Knoten nach oben und die Prüfung, ob jeder Vorfahre bereits in der Menge oder der Liste vorhanden ist, dauert O(h) Zeit, wobei h die Höhe des Binärbaums ist.
Im schlimmsten Fall beträgt die Höhe des Binärbaums O(n), wenn der Binärbaum schief ist. Daher beträgt die Gesamtzeitkomplexität des gegebenen Codes O(n) + O(n) + O(n) = O(n).
Raumkomplexität: O(n),
Die räumliche Komplexität des gegebenen Codes beträgt im schlimmsten Fall O(n). Dies liegt daran, dass die Größe der für jeden Knoten im Baum erstellten übergeordneten Karte O(n) beträgt. Darüber hinaus kann die Menge der Vorfahren im schlimmsten Fall auch alle Knoten im Binärbaum enthalten, was ebenfalls O(n) Platz beansprucht. Schließlich benötigt die zum Durchlaufen des Binärbaums verwendete Warteschlange O(n) Platz. Daher ist die Gesamtkomplexität des gegebenen Codes O(n) + O(n) + O(n) = O(n).
Wir haben eine effiziente Lösung zum Auffinden von LCA im binären Suchbaum besprochen. Im binären Suchbaum können wir mithilfe von BST-Eigenschaften LCA in O(h)-Zeit finden, wobei h die Höhe des Baums ist. Eine solche Implementierung ist im Binärbaum nicht möglich, da die Schlüsselknoten des Binärbaums keiner Reihenfolge folgen.
Vielleicht möchten Sie auch die folgenden Artikel sehen:
LCA mit Parent Pointer
Niedrigster gemeinsamer Vorfahre in einem binären Suchbaum.
Finden Sie LCA im Binärbaum mit RMQ
