Der Luhn-Algorithmus, auch bekannt als Modul 10 oder gegen 10 Der Algorithmus ist eine einfache Prüfsummenformel, die zur Validierung verschiedener Identifikationsnummern verwendet wird, z. B. Kreditkartennummern, IMEI-Nummern und kanadische Sozialversicherungsnummern. Die LUHN-Formel wurde Ende der 1960er Jahre von einer Gruppe Mathematiker entwickelt. Kurz darauf übernahmen es Kreditkartenunternehmen. Da der Algorithmus gemeinfrei ist, kann er von jedem verwendet werden. Die meisten Kreditkarten und viele staatliche Identifikationsnummern verwenden den Algorithmus als einfache Methode, um gültige Nummern von falsch eingegebenen oder anderweitig falschen Nummern zu unterscheiden. Es wurde entwickelt, um vor versehentlichen Fehlern und nicht vor böswilligen Angriffen zu schützen.
Schritte des Luhn-Algorithmus
Lassen Sie uns den Algorithmus anhand eines Beispiels verstehen:
Betrachten Sie das Beispiel einer Kontonummer 79927398713 .
Schritt 1 – Beginnen Sie mit der Ziffer ganz rechts und verdoppeln Sie den Wert jeder zweiten Ziffer.
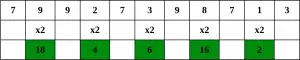
Schritt 2 – Wenn die Verdoppelung einer Zahl eine zweistellige Zahl ergibt, also größer als 9 (z. B. 6 × 2 = 12), dann addieren Sie die Ziffern des Produkts (z. B. 12: 1 + 2 = 3, 15: 1 + 5 =). 6), um eine einstellige Zahl zu erhalten.

Schritt 3 – Bilden Sie nun die Summe aller Ziffern.
Absicht Absicht

Schritt 4 – Wenn die Summe Modulo 10 gleich 0 ist (wenn die Summe mit Null endet), dann ist die Zahl gemäß der Luhn-Formel gültig; andernfalls ist es ungültig.

Da die Summe 70 beträgt, also ein Vielfaches von 10, ist die Kontonummer möglicherweise gültig.
Die Idee ist einfach; Wir durchqueren vom Ende. Für jede zweite Ziffer verdoppeln wir sie, bevor wir sie hinzufügen. Wir addieren zwei Ziffern der nach der Verdoppelung erhaltenen Zahl.
Implementierung:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
1 von 1000,00
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
tostring Java-Methode
C#
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)> >{> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
>
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
dhl bedeutet was
>
>Ausgabe
This is a valid card>
Der Luhn-Algorithmus erkennt jeden einzelnen Ziffernfehler sowie fast alle Vertauschungen benachbarter Ziffern.
