Das Trägheitsmoment ist die Eigenschaft eines Körpers in Rotationsbewegung. Das Trägheitsmoment ist die Eigenschaft der Rotationskörper, die dazu neigt, der Änderung der Rotationsbewegung des Körpers entgegenzuwirken. Sie ähnelt der Trägheit eines jeden Körpers in translatorischer Bewegung. Mathematisch ergibt sich das Trägheitsmoment aus der Summe des Produkts aus der Masse jedes Teilchens und dem Quadrat des Abstands von der Rotationsachse. Es wird in der Einheit gemessen kgm 2 .
Im folgenden Artikel erfahren Sie mehr über das Trägheitsmoment.
Inhaltsverzeichnis
- Definition des Trägheitsmoments
- Formel für das Trägheitsmoment
- Faktoren, die das Trägheitsmoment beeinflussen
- Wie berechnet man das Trägheitsmoment?
- Formel für das Trägheitsmoment für verschiedene Formen
- Gyrationsradius
- Trägheitsmomentsätze
- Trägheitsmomente für verschiedene Objekte
Definition des Trägheitsmoments
Das Trägheitsmoment ist die Tendenz eines Körpers in Rotationsbewegung, die der Änderung seiner Bewegung entgegenwirkt Drehbewegung aufgrund äußerer Kräfte. Das Trägheitsmoment verhält sich wie eine Winkelmasse und wird Rotationsträgheit genannt. Das Trägheitsmoment ist analog zum mechanischen Trägheit vom Körper.
MOI ist definiert als die Menge, die durch die Summe des Produkts ausgedrückt wird Masse jedes Teilchens mit dem Quadrat seines Abstands von der Rotationsachse für jedes Teilchen, das die Rotationsbewegung ausführt.
Einheit des Trägheitsmoments
Das Trägheitsmoment ist eine skalare Größe und die SI-Einheit des Trägheitsmoments ist kgm 2 .
Dimensionsformel für das Trägheitsmoment
Denn das Trägheitsmoment ist das Produkt aus Masse und Abstandsquadrat. Es ist Dimensionsformel ergibt sich aus dem Produkt der Maßformel der Masse und dem Quadrat der Maßformel der Länge. Die Dimensionsformel des Trägheitsmoments lautet: ML 2
Was ist Trägheit?
Trägheit ist die Eigenschaft einer Materie, aufgrund derer sie dazu neigt, der Änderung ihres Bewegungszustands Widerstand zu leisten. Das bedeutet, dass ein Körper in Ruhe versucht, in Ruhe zu bleiben und jeder Kraft zu widerstehen, die versucht, ihn in Bewegung zu versetzen, und ein Körper in Bewegung versucht, in Bewegung zu bleiben und jeder Kraft zu widerstehen, die versucht, ihn dazu zu bringen, die Größe seiner Bewegung zu ändern. Sie entspricht mengenmäßig der maximalen Kraft, die versucht, ihren Zustand zu ändern Bewegung .
Lerne mehr über Trägheit .
Formel für das Trägheitsmoment
Das Trägheitsmoment ist a Skalare Größe . Mathematisch wird das Produkt aus dem Quadrat der Masse eines Teilchens und dem Abstand von der Rotationsachse als Trägheitsmoment des Teilchens um die Rotationsachse bezeichnet.
Die allgemeine Formel zum Ermitteln des Trägheitsmoments eines beliebigen Objekts lautet:
Ich = Herr 2
Wo,
M ist die Masse des Objekts‘
R ist der Abstand von der Rotationsachse
Für einen Körper, der aus kontinuierlichen, unendlich kleinen Teilchen besteht, wird die Integralform des Trägheitsmoments zur Berechnung des Trägheitsmoments verwendet.
I = ∫dI
Ich =
int_{0}^{M} r^2 dm
Trägheitsmoment eines Teilchensystems
Das Trägheitsmoment eines Teilchensystems ergibt sich aus der Formel:
I = ∑m ich R ich 2
Wo,
R ich ist der senkrechte Abstand des iThTeilchen von der Achse
M ich ist die Masse von iThPartikel
Die obige Gleichung für das Trägheitsmoment besagt, dass das Trägheitsmoment für ein Teilchensystem gleich der Summe des Produkts aus der Masse jedes einzelnen Teilchens und dem Quadrat des Abstands von der Rotationsachse jedes Teilchens ist.
Für die unten angegebene Abbildung gilt:
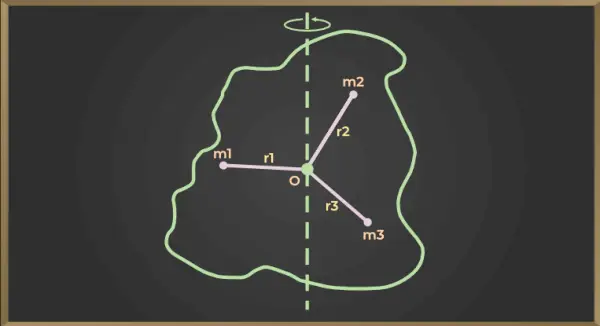
Trägheitsmoment des ersten Teilchens = m1×r12
Trägheitsmoment des zweiten Teilchens = m2×r22
Trägheitsmoment des dritten Teilchens = m3×r32
Ähnlich,
Trägheitsmoment von nThTeilchen = mN×rN2
Nun das Trägheitsmoment des gesamten Körpers um die Rotationsachse AB wird gleich der Summe der Trägheitsmomente aller Teilchen sein, also
Ich = m1×r12+ m2×r22+ m3×r32+……+mN×rN2
Javac wird nicht erkannt
I = Σm ich ×r ich 2
Wo,
ICH stellen das Trägheitsmoment des Körpers um die Rotationsachse dar
M ich ist die Masse von iThPartikel,
R ich ist der Radius von iThPartikel
S stellt die Summe dar.
Aus der Gleichung können wir sagen, dass das Trägheitsmoment eines Körpers um eine feste Achse gleich der Summe des Produkts aus der Masse jedes einzelnen Teilchens dieses Körpers und dem Quadrat seines senkrechten Abstands von der festen Achse ist.
Faktoren, die das Trägheitsmoment beeinflussen
Das Trägheitsmoment eines Objekts hängt von den folgenden Werten ab:
- Form und Größe des Objekts
- Dichte des Materials des Objekts
- Drehachse
Wie berechnet man das Trägheitsmoment?
Es werden mehrere Methoden verwendet Berechnen Sie das Trägheitsmoment eines rotierenden Objekts.
- Für gleichförmige Objekte wird das Trägheitsmoment berechnet, indem man das Produkt seiner Masse mit dem Quadrat seines Abstands von der Rotationsachse (r) bildet2).
- Für ungleichmäßige Objekte berechnen wir das Trägheitsmoment, indem wir die Summe des Produkts der einzelnen Punktmassen bei jedem unterschiedlichen Radius bilden. Die hierfür verwendete Formel lautet
I = ∑m ich R ich 2
Formel für das Trägheitsmoment für verschiedene Formen
In dieser Tabelle werden Ausdrücke für das Trägheitsmoment einiger symmetrischer Objekte zusammen mit ihrer Rotationsachse erläutert:

| Objekt | Achse | Ausdruck des Trägheitsmoments |
|---|---|---|
| Hohlzylinder dünnwandig | Zentral | Ich = Herr2 |
| Dünner Ring | Durchmesser | Ich = 1/2 Herr2 |
| Ringförmiger Ring oder Hohlzylinder | Zentral | I = 1/2 M(r22+ r12) |
| Massiver Zylinder | Zentral | Ich = 1/2 Herr2 |
| Einheitliche Scheibe | Durchmesser | I = 1/4 Herr2 |
| Hohlkugel | Zentral | I = 2/3 Herr2 |
| Feste Kugel | Zentral | I = 2/5 Herr2 |
| Einheitliche symmetrische Kugelschale | Zentral | |
| Einheitliche Platte oder rechteckiges Parallelepiped | Zentral | I = 1/12 M(a2+ b2) |
| Dünner Stab | Zentral | I = 1/12 Mr2 |
| Dünner Stab | Am Ende von Rod | Ich = 1/3 Herr2 |
Gyrationsradius
Der Gyrationsradius eines Körpers ist definiert als der senkrechte Abstand von der Rotationsachse zum Massenpunkt, dessen Masse gleich der Masse des gesamten Körpers ist und dessen Trägheitsmoment gleich dem tatsächlichen Trägheitsmoment des Objekts in seiner jetzigen Form ist angenommen, dass dort die Gesamtmasse des Körpers konzentriert ist. Es ist eine imaginäre Entfernung. Der Gyrationsradius wird mit K bezeichnet.
Wenn die Masse und der Trägheitsradius des Körpers M bzw. K betragen, dann beträgt das Trägheitsmoment eines Körpers
Ich = MK 2 ……(1)
Somit steht der Trägheitsradius eines Körpers senkrecht zur Rotationsachse, deren Quadrat multipliziert mit der Masse dieses Körpers das Trägheitsmoment dieses Körpers um diese Achse ergibt.
Wiederum nach Gleichung (1), K2= I/M
K = √(I/m)
Somit ist der Rotationsradius eines Körpers um eine Achse gleich der Quadratwurzel des Verhältnisses des Körpers um diese Achse.
Trägheitsmomentsätze
Es gibt zwei Arten von Theoremen, die im Hinblick auf das Trägheitsmoment sehr wichtig sind:
- Satz der parallelen Achse
- Satz der senkrechten Achse
Satz der senkrechten Achse
Satz der senkrechten Achse besagt, dass die Summe des Trägheitsmoments eines Körpers um zwei zueinander senkrechte Achsen, die in der Ebene eines Körpers liegen, gleich dem Trägheitsmoment des Körpers um die dritte Achse ist, die senkrecht zu den beiden Achsen steht und durch deren Punkt verläuft der Kreuzung.

In der obigen Abbildung ist OCHSE Und GMBH sind zwei Achsen in der Körperebene, die senkrecht zueinander stehen. Die dritte Achse ist OZ die senkrecht zur Körperebene steht und durch den Schnittpunkt der verläuft OCHSE Und GMBH Achsen. Wenn ICH X , ICH Und , Und ICH Mit sind die Trägheitsmomente des Körpers um die Achse OCHSE , GMBH , Und OZ Achsen bzw., dann nach diesem Satz
ICH X + Ich Und = Ich Mit
Satz der parallelen Achse
Entsprechend Satz der parallelen Achse , das Trägheitsmoment eines Körpers um eine gegebene Achse ist die Summe des Trägheitsmoments um eine Achse, die durch den Massenschwerpunkt dieses Körpers verläuft, und dem Produkt aus dem Quadrat der Masse des Körpers und dem senkrechten Abstand zwischen den zwei Achsen.

In der obigen Abbildung müssen wir das Trägheitsmoment von ermitteln ICH Ö des Körpers, der durch den Punkt geht Ö und um die Achse senkrecht zur Ebene, während das Trägheitsmoment des Körpers durch den Massenschwerpunkt verläuft C und um eine Achse, die parallel zur gegebenen Achse ist ICH C , dann nach diesem Satz
ICH Ö = Ich C + Ml 2
Wo
M ist die Masse des gesamten Körpers
l ist der senkrechte Abstand zwischen zwei Achsen.
Trägheitsmomente für verschiedene Objekte
Das Trägheitsmoment verschiedener Objekte wird weiter unten in diesem Artikel besprochen
Trägheitsmoment einer rechteckigen Platte
Wenn die Masse der Platte M, die Länge l und die Breite b beträgt, dann verläuft das Trägheitsmoment durch den Schwerpunkt und um eine Achse senkrecht zur Plattenebene.

I = M(l 2 + b 2 / 12)
Trägheitsmoment einer Scheibe
Wenn die Scheibe eine Masse M und einen Radius r hat, beträgt das Trägheitsmoment um die geometrische Achse der Scheibe

I = 1/2(Mr 2 )
Trägheitsmoment einer Stange
Wenn die Masse des Stabes M und die Länge l ist, dann ist das Trägheitsmoment um die Achse senkrecht zur Länge des Stabes und durch seinen Schwerpunkt

Ich = ML 2 /12
Trägheitsmoment eines Kreises
Wenn die Masse des Rings M und der Radius des Rings r ist, dann beträgt das Trägheitsmoment um die Achse, die senkrecht durch den Mittelpunkt des Rings verläuft
Python-Liste initialisieren

Ich = Herr 2
Trägheitsmoment einer Kugel
Wenn eine feste Kugel eine Masse von M und einen Radius von r hat, dann beträgt das Trägheitsmoment um ihren Durchmesser

I = 2/5Mr 2
Trägheitsmoment eines Vollzylinders
Das Trägheitsmoment eines Vollzylinders mit Radius „R“ und Masse M ist gegeben durch

I = 1/2MR 2
Trägheitsmoment des Hohlzylinders
Ein Hohlzylinder hat zwei Radien, nämlich den Innenradius und den Außenradius. Das Trägheitsmoment eines Hohlzylinders mit der Masse M und dem Außenradius R1und Innenradius R2ist gegeben als

I = 1/2M(R 1 2 + R 2 2 )
Trägheitsmoment einer festen Kugel
Das Trägheitsmoment einer festen Kugel mit der Masse „M“ und dem Radius „R“ wird wie folgt angegeben:

I = 2/5MR 2
Trägheitsmoment der Hohlkugel
Das Trägheitsmoment einer Hohlkugel mit der Masse M und dem Radius „R“ wird wie folgt angegeben:

I = 2/3MR 2
Trägheitsmoment des Rings
Das Trägheitsmoment eines Rings wird für zwei Fälle angegeben, wenn die Drehachse durch die Mitte und durch den Durchmesser verläuft.
Das Trägheitsmoment des Rings um die durch den Mittelpunkt verlaufende Achse ist gegeben durch
Konvertieren Sie einen String in einen Int

Ich = HERR 2
Das Trägheitsmoment des Rings um die durch den Durchmesser verlaufende Achse ist gegeben durch

Ich = Herr 2 /2
Trägheitsmoment des Quadrats
Das Trägheitsmoment des Quadrats der Seite „a“ wird wie folgt angegeben:

Ich = a 4 /12
Das Trägheitsmoment einer quadratischen Platte mit der Seitenlänge „l“ und der Masse M wird wie folgt angegeben:
I = 1/6ML 2
Trägheitsmoment des Dreiecks
Das Trägheitsmoment eines Dreiecks wird für drei Situationen angegeben: erstens, wenn die Achse durch die Mitte verläuft, zweitens, wenn die Achse durch die Basis verläuft und drittens, wenn die Achse senkrecht zur Basis verläuft. Sehen wir uns die Formel einzeln an. Für ein Dreieck mit der Basis „b“ und der Höhe „h“ lautet die Formel für das Trägheitsmoment wie folgt

Wenn die Achse durch den Schwerpunkt verläuft
Ich = bh 3 /36
Wenn die Achse durch die Basis verläuft
Ich = bh 3 /12
Wenn die Achse senkrecht zur Basis steht
I = (hb/36)(b 2 - B 1 b + b 1 2 )
Unterschied zwischen Trägheitsmoment und Trägheit
Der Unterschied zwischen Trägheit und Trägheitsmoment ist unten tabellarisch aufgeführt:
| Ja Nein. | Trägheit | Trägheitsmoment |
|---|---|---|
| 1. | Seine Bedeutung liegt in der linearen Bewegung. | Seine Bedeutung liegt in der Rotationsbewegung. |
| 2. | Es ist die Eigenschaft eines Objekts, die der Zustandsänderung des Objekts bei linearer Bewegung entgegenwirkt. | Das Trägheitsmoment ist die Eigenschaft eines Gegenstandes, die der Zustandsänderung des Gegenstandes bei Drehbewegung entgegenwirkt. |
| 3. | Die Trägheit eines Objekts hängt nur von seiner Masse ab. | Das Trägheitsmoment eines Objekts hängt von seiner Masse und seiner Massenverteilung relativ zur Rotationsachse ab. |
| 4. | Die Trägheit eines Objekts ist fest. | Das Trägheitsmoment eines Objekts variiert in Bezug auf verschiedene Drehachsen. |
Kinetische Energie eines rotierenden Körpers
Nehmen wir einen Körper der Masse „m“ an, der mit der Geschwindigkeit v im Abstand „r“ von der Rotationsachse rotiert. Seine Winkelgeschwindigkeit ist dann gegeben durch ω = v/r, dann v = rω. Jetzt wissen wir, dass die Kinetische Energie eines Körpers ist gegeben durch
KE = 1/2mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2Oh2
⇒ KE = 1/2Iω 2
Daher ergibt sich die kinetische Energie eines rotierenden Körpers aus der Hälfte des Produkts aus dem Trägheitsmoment und dem Winkelgeschwindigkeit vom Körper. Die kinetische Energie eines rotierenden Körpers wird auch als kinetische Energie bezeichnet Rotationskinetische Energie . Die Formel der Rotationskinetischen Energie lautet:
KE = 1/2Iω 2
Das Trägheitsmoment (I) ist unabhängig von der Winkelgeschwindigkeit des Körpers. Sie ist eine Funktion der Masse des rotierenden Körpers und des Abstands des Körpers von der Rotationsachse. Daher beobachten wir, dass die Winkelbewegung der linearen Bewegung analog ist. Das bedeutet, dass die Bedeutung des Trägheitsmoments darin besteht, dass es eine Vorstellung davon gibt, wie Massen in unterschiedlichen Abständen von der Rotationsachse in einem rotierenden Körper verteilt sind.
Anwendung des Trägheitsmoments
Das Trägheitsmoment hat verschiedene Anwendungen, von denen einige im Folgenden erläutert werden:
- Aufgrund des größeren Trägheitsmoments dreht sich die Erde mit der gleichen Winkelgeschwindigkeit um ihre Achse.
- Unter dem Kinderspielmotor ist ein kleines bewegliches Rad angebracht. Nach dem Reiben dieses Rades mit dem Boden und dem Verlassen des Motors läuft der Motor aufgrund des Trägheitsmoments des Rades noch einige Zeit weiter.
- Jeder Motor besteht aus einem großen und schweren Rad, das an seiner Welle befestigt ist und dessen Masse den größten Teil auf seinem Umfang verteilt. Daher ist sein Trägheitsmoment hoch. Dieses Rad wird Schwungrad genannt. Das Drehmoment, das die Welle des Motors antreibt, nimmt immer weiter zu. Daher ist die Drehung der Welle möglicherweise nicht gleichmäßig, aber aufgrund des Vorhandenseins eines beweglichen Rades mit größerer Trägheit dreht sich die Welle weiterhin mit nahezu gleichmäßiger Geschwindigkeit.
- Im Rad von Ochsenkarren, Rikschas, Motorrollern, Fahrrädern usw. ist der größte Teil der Masse auf dessen Kreis bzw. Felge konzentriert. Dieser Reifen oder diese Routine ist durch starre Speichen an der Radachse befestigt. Dadurch erhöht sich sein Trägheitsmoment. Wenn sich die Beine beim Radfahren nicht mehr bewegen, dreht sich das Rad daher noch einige Zeit weiter.
Überprüfen Sie auch
- Kinematik der Rotationsbewegung
- Bewegung eines starren Körpers
- Rollbewegung
Gelöste Beispiele zu Trägheitsmomenten
Beispiel 1: Ein Körper mit der Masse 500 g rotiert um eine Achse. Der Abstand des Körperschwerpunkts von der Rotationsachse beträgt 1,2 m. Finden Sie das Trägheitsmoment des Körpers um die Rotationsachse.
Lösung:
Vorausgesetzt, dass M = 500 g = 0,5 kg, r = 1,2 m.
Offensichtlich kann man davon ausgehen, dass die gesamte Masse eines Körpers in seinem Massenschwerpunkt liegt. Dann das Trägheitsmoment des Körpers um die Rotationsachse.
Ich = Herr2
I = 0,5 × (1,2)2
I = 0,72 kg m2
Beispiel 2: Der Rotationsradius um eine 12 cm vom Massenschwerpunkt entfernte Achse eines Körpers mit der Masse 1,2 kg beträgt 13 cm. Berechne das Rotationsradius und Trägheitsmoment um eine Achse, die durch den Massenschwerpunkt verläuft.
Lösung:
Vorausgesetzt, M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, ICM= ?
Aus dem Satz der parallelen Achse I = ICM+ Ml2
K2= KCM2+ l2
oder KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
Typumwandlung und Typkonvertierung in JavaNun, Trägheitsmoment ICM= MKCM2
ICHCM= 1,0 × (0,05)2= 2,5 × 10-3kg m2
Beispiel 3: Ein Körper mit der Masse 0,1 kg dreht sich um eine Achse. Wenn der Abstand des Massenschwerpunkts des Körpers von der Rotationsachse 0,5 m beträgt, ermitteln Sie das Trägheitsmoment des Körpers.
Lösung:
Vorausgesetzt, M = 0,1 kg und r = 0,5 m
also ich = Herr2
I = 0,1 × (0,5)2
I = 0,025 kg m2
Beispiel 4: Das Trägheitsmoment der Ringe um eine Achse, die durch ihren Mittelpunkt senkrecht zur Ebene des Kreisrings verläuft, beträgt 200 gm cm 2 . Wie groß wird das Trägheitsmoment um seinen Durchmesser sein?
Lösung:
Trägheitsmoment eines Kreisrings um eine Achse, die durch einen anderen Mittelpunkt senkrecht zu seiner Ebene verläuft
HERR2= 200 g/cm2
Trägheitsmoment etwa zum Durchmesser
= 1/2 HERR2
= 1/2 × 200 = 100 g cm2
FAQs zu Trägheitsmomenten
Wie berechnet man das Trägheitsmoment?
Die Grundformel zum Ermitteln des Trägheitsmoments eines gleichförmigen Objekts lautet:
Ich = Herr 2
Wo,
M ist die Masse des Objekts‘
R ist der Abstand von der Rotationsachse
Wie berechnet man das Trägheitsmoment eines Balkens?
Das Trägheitsmoment eines Balkens entlang der Mitte und der dazu horizontalen Achse wird mit der Formel berechnet:
Ich = ML 2 / 12
Wovon hängt das Trägheitsmoment eines Körpers ab?
Das Trägheitsmoment eines Objekts hängt von den folgenden Faktoren ab:
- Masse des Körpers,
- Drehachse
- Form und Größe des Objekts
Was ist die Einheit des Trägheitsmoments?
Die Einheit des Trägheitsmoments ist Kgm 2
Kann das Trägheitsmoment negativ sein?
Nein, das Trägheitsmoment kann niemals negativ sein.
Was ist das Massenträgheitsmoment?
Das Massenträgheitsmoment ist die Messung des Widerstands eines Körpers gegenüber einer Änderung seines Drehimpulses oder seiner Richtung. Das Massenträgheitsmoment für eine Punktmasse ist gegeben durch I = mr2und für ein Teilchensystem ist das Massenträgheitsmoment gegeben als I = ΣichMichRich2
Was ist das Flächenträgheitsmoment?
Das Flächenträgheitsmoment ist eine Eigenschaft einer zweidimensionalen Formebene, die zeigt, wie Punkte in Bezug auf eine beliebige Achse in einer Ebene verteilt sind. Das Flächenträgheitsmoment wird auch als Zweites Flächenmoment oder Quadratisches Flächenmoment bezeichnet. Die Formel für das Flächenträgheitsmoment in der xy-Ebene lautet Ixy= ∫xy dxdxy = ∫xy dA
