Was ist eine Steigung?

Eine Anzahl absoluter Werte, die darstellen, ob eine Linie vorhanden ist steiler oder flacher und das Richtung der Linie im Diagramm werden als a bezeichnet Steigung oder Gefälle. Die Steigung einer Geraden ist ein grundlegendes Konzept in den Wirtschaftswissenschaften und der Mathematik. Es wird im Allgemeinen mit dem Buchstaben bezeichnet 'M'. Die Steigung kann durch Division berechnet werden „vertikale Veränderung“ mit dem „horizontale Veränderung“ zwischen zwei verschiedenen Punkten auf einer Linie.

PISTENARTEN

Es gibt zwei Hauptarten von Pisten, die im Folgenden aufgeführt sind:

Positive Steigung:Eine Steigung, bei der zwei Variablen, d. h. eine Variable auf der x-Achse und eine Variable auf der y-Achse, a zeigen gute Beziehung ist bekannt als positive Steigung. Einfacher ausgedrückt handelt es sich bei einer positiven Steigung um eine Steigung, bei der die Variable x mit der Zunahme der Variablen y zunimmt und/oder die Variable y mit der Zunahme der Variablen x zunimmt. Ebenso nimmt die Variable x mit der Abnahme der Variablen y ab und/oder die Variable y nimmt mit der Abnahme der Variablen x ab. Das bedeutet, dass beide Variablen vorhanden sind Ergänzungen zueinander. Eine positive Steigung bewegt sich im Richtung nach oben oder ist ansteigenden.
Grafisch ausgedrückt ist eine positive Steigung eine Steigung, bei der die Linie im Diagramm ansteigt, wenn sie sich von links nach rechts bewegt. Das Konzept der positiven Steigung kann mit Hilfe von klar verstanden werden Angebotskurve eines Produzenten oder Unternehmens in der Wirtschaft. Die beiden Variablen der Kurve sind der Preis auf der y-Achse und die Warenmenge auf der x-Achse. Nehmen wir an, dass das Unternehmen die Waren herstellt Gewinnmaximierung. Wenn also die Preise der Güter steigen, erhöht sich auch die vom Unternehmen angebotene Menge dieser Güter, während bei sinkenden Preisen die vom Unternehmen angebotene Menge sinkt. Mit anderen Worten: Bei höheren Preisen wird das Unternehmen oder der Produzent die angebotene Menge erhöhen, um mehr Gewinn zu erzielen, während es bei niedrigeren Preisen die angebotene Menge reduziert, um den Verlust zu verringern. Es zeigt sich also, dass die Preise und die angebotene Menge in einem positiven Zusammenhang zueinander stehen, was aus dem untenstehenden Diagramm ersichtlich ist:
Negative Steigung:Eine Steigung, bei der zwei Variablen, d. h. eine Variable auf der x-Achse und eine Variable auf der y-Achse, a zeigen negative Beziehung ist bekannt als negative Steigung. Mit anderen Worten ist eine negative Steigung eine Steigung, bei der die Variable x mit der Abnahme der Variablen y zunimmt und/oder die Variable y mit der Abnahme der Variablen x zunimmt. Auf die gleiche Weise nimmt die Variable x mit der Zunahme der Variablen y ab und/oder die Variable y nimmt mit der Zunahme der Variablen x ab. Dies stellt eine dar umgekehrte Beziehung zwischen diesen beiden Variablen. Eine negative Steigung bewegt sich im Abwärtsrichtung oder ist absteigend.
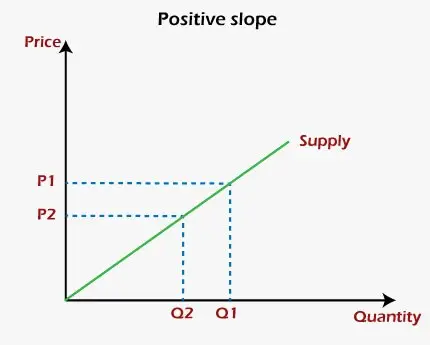
Grafisch gesehen ist eine negative Steigung eine Steigung, bei der die Linie im Diagramm abfällt, wenn sie sich von links nach rechts bewegt. Eines der besten Beispiele für die negative Steigung des Diagramms ist das Nachfragekurve In Wirtschaft. Die beiden Variablen der Kurve sind der Preis auf der y-Achse und die Warenmenge auf der x-Achse. Wie wir wissen, kaufen Verbraucher eine große Menge eines Gutes zu einem niedrigeren Preis als zu einem höheren Preis. Daher nimmt die von den Verbrauchern nachgefragte Menge an Gütern mit steigenden Preisen dieser Güter ab. Wenn andererseits die Preise der Güter sinken, steigt die Mengennachfrage. Daher zeigt es a negative Beziehung zwischen den Preisen und der gelieferten Menge dieser Waren. Dies lässt sich anhand des untenstehenden Diagramms verdeutlichen:

ZWEI WEITERE PISTENARTEN

Neben positiven und negativen Steigungen gibt es zwei weitere Arten von Steigungen: Nullsteigung und unendliche Steigung. Sie können aus der gegebenen Erklärung verstanden werden:

Nullsteigung:Ein Zustand, bei dem die Variable auf der y-Achse bei der Änderung der Variablen auf der x-Achse gleich bleibt, wird als bezeichnet Steigung von Null. Grafisch gesehen, a horizontale oder flache Linie im Diagramm hat eine Steigung von Null. Daher heißt es a konstante Funktion. Eine Steigung von Null bewegt sich weder nach oben noch nach unten. Es bewegt sich nur nach links oder rechts.
Das folgende Diagramm ist eine grafische Darstellung der Nullsteigung:
Unendliche Steigung:Ein Zustand, bei dem die Variable auf der x-Achse bei der Änderung der Variablen auf der y-Achse gleich bleibt, wird als bezeichnet unendliche Steigung. Es wird auch das genannt undefinierte Steigung. Gemäß den grafischen Bedingungen a vertikale oder senkrechte Linie im Diagramm hat eine unendliche Steigung. Eine unendliche Neigung bewegt sich weder nach links noch nach rechts. Es zeigt eine Bewegung nur in Aufwärts- oder Abwärtsrichtung.
Im folgenden Diagramm ist eine unendliche Steigung dargestellt:

BERECHNUNG DER NEIGUNG

• In einer linearen Gleichung von ax + by + c = 0, Die Steigung ist definiert als -a/b.
• Die Geradengleichung kann mit Hilfe des berechnet werden Punkt-Steigungsformel wenn beide die Steigung M einer Linie und eines Punktes (x1, y1) sind bekannt. Die Formel ist unten angegeben:
  y - y1 = m (x - x1)
• Die zweizeilige wird sein parallel wenn ihre Steigungen sind gleich, während zwei Zeilen sein werden aufrecht wenn das Produkt ihrer Steigungen ist -1.

WEITERE INFORMATIONEN

• Der Absolutwert der Steigung wird verwendet, um herauszufinden, ob eine Kurve vorhanden ist steiler oder flacher.
• Der positive und negative Wert der Steigung bestimmt die Richtung, d. h. nach oben oder unten, des Hanges.
• Es entsteht eine Kurve steiler mit der Zunahme des Absolutwerts der Steigung.
• Es entsteht eine Kurve geschmeichelt mit der Abnahme des Absolutwerts der Steigung.
• Diese Bedingungen werden dadurch nicht berührt negative oder positive Steigung (nicht der negative oder positive Wert).
• A geringere positive Steigung bedeutet, dass eine flachere, nach oben geneigte Kurve entsteht.
• A höhere positive Steigung bedeutet, dass eine steilere, nach oben gebogene Kurve entsteht.
• A negative Steigung mit großem Absolutwert bedeutet, dass eine steilere, nach unten geneigte Kurve entsteht.
• A negative Steigung mit kleinerem Absolutwert bedeutet, dass eine flachere, nach unten gebogene Kurve entsteht.