Finden Sie bei einer gegebenen Zeichenfolge alle Möglichkeiten, die angegebene Zeichenfolge in Klammerform zu unterbrechen. Schließen Sie jede Teilzeichenfolge in Klammern ein.
Inselbuchstabe Java
Beispiele:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Wir empfehlen Ihnen dringend, Ihren Browser zu minimieren und dies zunächst selbst zu versuchen.
Die Idee ist, Rekursion zu verwenden. Wir pflegen zwei Parameter – den Index des nächsten zu verarbeitenden Zeichens und die bisher ausgegebene Zeichenfolge. Wir beginnen mit dem Index des nächsten zu verarbeitenden Zeichens, hängen die durch die unverarbeitete Zeichenfolge gebildete Teilzeichenfolge an die Ausgabezeichenfolge an und führen eine Rekursion über die verbleibende Zeichenfolge durch, bis wir die gesamte Zeichenfolge verarbeitet haben. Wir verwenden std::substr, um den Ausgabestring zu bilden. substr(pos n) gibt einen Teilstring der Länge n zurück, der an Position pos des aktuellen Strings beginnt.
Das folgende Diagramm zeigt den Rekursionsbaum für die Eingabezeichenfolge „abc“. Jeder Knoten im Diagramm zeigt eine verarbeitete Zeichenfolge (grün markiert) und eine unverarbeitete Zeichenfolge (rot markiert).
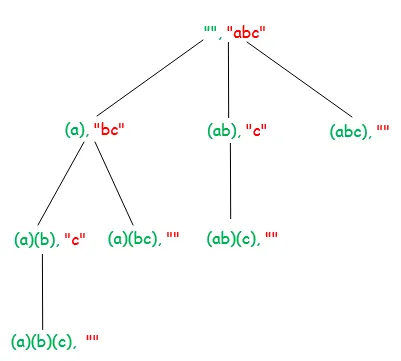
Dateisystem unter Linux
Nachfolgend finden Sie die Umsetzung der obigen Idee
C++// C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include
// Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations(String str int index String out) { if (index == str.length()) System.out.println(out); for (int i = index; i < str.length(); i++) // append substring formed by str[index // i] to output string findCombinations(str i + 1 out + '(' + str.substring(index i+1) + ')' ); } // Driver Code public static void main (String[] args) { // input string String str = 'abcd'; findCombinations(str 0 ''); } } // Contributed by Pramod Kumar
# Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations(string index out): if index == len(string): print(out) for i in range(index len(string) 1): # append substring formed by str[index # i] to output string findCombinations(string i + 1 out + '(' + string[index:i + 1] + ')') # Driver Code if __name__ == '__main__': # input string string = 'abcd' findCombinations(string 0 '') # This code is contributed by # sanjeev2552
// C# program to find all combinations // of Non-overlapping substrings formed // from given string using System; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations(string str int index string @out) { if (index == str.Length) { Console.WriteLine(@out); } for (int i = index; i < str.Length; i++) { // append substring formed by // str[index i] to output string findCombinations( str i + 1 @out + '(' + str.Substring(index (i + 1) - index) + ')'); } } // Driver Code public static void Main(string[] args) { // input string string str = 'abcd'; findCombinations(str 0 ''); } } // This code is contributed by Shrikant13
// Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations(string index out) { if (index == string.length) { console.log(out); } for (let i = index; i < string.length; i++) { // append substring formed by str[index // i] to output string findCombinations(string i + 1 out + '(' + string.substring(index i + 1) + ')'); } } // Driver Code const string = 'abcd'; findCombinations(string 0 ''); // contributed by adityasharmadev01
Ausgabe
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Zeitkomplexität: O(N2)
Hilfsraum: O(N2)
Arten von Binärbäumen
