Quadrant ist definiert als ein Bereich im Raum, der durch zwei Achsen, nämlich die X-Achse und die Y-Achse in der kartesischen Ebene, in vier gleiche Teile geteilt wird. Diese beiden Achsen schneiden einander im 90-Grad-Winkel und die vier so gebildeten Regionen werden vier Quadranten genannt, nämlich I-Quadrant, II-Quadrant, III-Quadrant und IV-Quadrant.
Arten von Binärbäumen
In diesem Artikel werden wir wesentliche Quadrantenkonzepte untersuchen, einschließlich dessen, was ein Quadrant ist, seiner Fläche, seines Quadrantengraphen, seiner kartesischen Ebene, der Vorzeichenkonventionen innerhalb des Quadranten, der Abszisse und der Koordinate sowie der Darstellung von Punkten auf einem Quadranten.
Inhaltsverzeichnis
- Was sind Quadranten des Graphen?
- Unterzeichnen Sie die Konvention in Quadranten
- Punkte auf Quadranten darstellen
- Trigonometrische Werte in verschiedenen Quadranten
Was sind Quadranten des Graphen?
Ein Quadrant ist ein ausgewiesener Bereich auf einem Kartesisches Flugzeug , entsteht durch den Schnittpunkt der X- und Y-Achsen. Auf dieser Ebene werden vier Quadranten gebildet, jeder mit seinen einzigartigen Merkmalen. Der erste Quadrant oben rechts hat positive x- und y-Koordinaten. Der zweite Quadrant oben links hat negative x- und positive y-Koordinaten usw. Das Verständnis dieser Quadranten ist für die Lokalisierung und Interpretation von Punkten im Diagramm von wesentlicher Bedeutung und bietet eine systematische Möglichkeit zur Navigation und Analyse kartesischer Koordinaten.
4 Quadranten auf der Koordinatenebene
Die kartesische Ebene, die durch die X- und Y-Achsen gebildet wird, ist in vier Quadranten mit jeweils unterschiedlichen Eigenschaften unterteilt:
- Erster Quadrant: Oben rechts sind sowohl die x- als auch die y-Koordinaten positiv. Dieser Quadrant repräsentiert Punkte im oberen rechten Teil der Ebene.
- Zweiter Quadrant: Die X-Koordinate befindet sich oben links und ist negativ und die Y-Koordinate positiv. Dieser Quadrant deckt Punkte im oberen linken Teil der Ebene ab.
- Dritter Quadrant: Unten links positioniert, sind sowohl die x- als auch die y-Koordinaten negativ. Punkte im unteren linken Bereich der Ebene fallen in diesen Quadranten.
- Vierter Quadrant: Unten rechts ist die x-Koordinate positiv und die y-Koordinate negativ. Dieser Quadrant umfasst Punkte im unteren rechten Teil der Ebene.
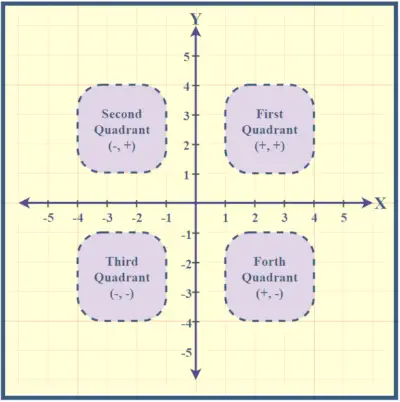
Die Nummerierung der Quadranten erfolgt entgegen dem Uhrzeigersinn, beginnend oben rechts. Der Punkt, an dem sich die X- und Y-Achsen schneiden, wird als Ursprung bezeichnet. Die Koordinaten (0,0) geben Nullwerte für x und y an. Das Verständnis dieser Quadranten hilft beim Auffinden von Punkten innerhalb der kartesischen Ebene.
Was ist Herkunft?
Der Ausgangspunkt eines Diagramms, der Ursprung genannt und als (0, 0) angezeigt wird, ist der Schnittpunkt der horizontalen x-Achse und der vertikalen y-Achse. Das bedeutet, dass im Ursprung die Werte für x und y Null sind. Er dient als Referenzpunkt zum Auffinden anderer Punkte im Diagramm. Im oben hinzugefügten Bild zeigt Punkt O den Ursprung.
Abszisse und Ordinate in Quadranten
In den vier Quadranten werden Zahlen als Paare (a, b) dargestellt, wobei „a“ für die x-Koordinate und „b“ für die y-Koordinate steht. Um herauszufinden, wo sich ein Punkt befindet, ohne ihn einzutragen, achten Sie auf die Vorzeichen der x-Koordinate (Abszisse) und der y-Koordinate (Ordinate). Wenn Sie beispielsweise einen Punkt wie Q (3, -5) haben, zeigen die Zeichen (+ve, -ve) an, dass er sich im Quadranten IV befindet.
Die Abszisse zeigt den horizontalen Abstand von der Y-Achse. Eine positive Abszisse bedeutet nach rechts, und in unserem Beispiel bedeutet Abszisse = 3, dass sie vom Ursprung entlang der x-Achse um 3 Einheiten nach rechts geht.
Die Ordinate gibt den vertikalen Abstand vom Ursprung an. Eine negative Ordinate bedeutet, dass man vom Ursprung entlang der y-Achse nach unten geht. Im Beispiel bedeutet Ordinate = -5, dass der Wert um 5 Einheiten nach unten geht.
Unterzeichnen Sie die Konvention in Quadranten
Die Zeichenkonventionen in den Quadranten können anhand des unten hinzugefügten Bildes leicht verstanden werden.

Wenn wir uns in der XY-Ebene entlang der x-Achse von links nach rechts bewegen, erhöht sich die x-Koordinate. Ebenso führt eine Bewegung entlang der Y-Achse von unten nach oben zu einer Vergrößerung der Y-Koordinate. Die XY-Ebene ist in vier Quadranten unterteilt, jeder mit spezifischen Vorzeichenkonventionen für x- und y-Koordinaten:
| Quadrant | x-Koordinate | y-Koordinate |
|---|---|---|
| 1. Quadrant | Positiv (+) | Positiv (+) |
| 2. Quadrant | Negativ (-) | Positiv (+) |
| 3. Quadrant | Negativ (-) | Negativ (-) |
| 4. Quadrant | Positiv (+) | Negativ (-) |
Daher haben Punkte im 1. Quadranten positive Werte für x und y, Punkte im 2. Quadranten haben ein negatives x und ein positives y, der 3. Quadrant hat sowohl negative x- als auch y-Werte und der 4. Quadrant hat ein positives x und ein negatives y.
Punkte auf Quadranten darstellen
In einer kartesischen Ebene werden Punkte durch die x-Achse und die y-Achse identifiziert. Diese Punkte werden als (a, b) bezeichnet, wobei „a“ die x-Koordinate (Abszisse) und „b“ die y-Koordinate (Ordinate) ist. Um einen Punkt in einem Quadranten zu positionieren, berücksichtigen wir die Vorzeichen dieser Koordinaten. Die Werte von x und y geben an, wie weit der Punkt von der x- bzw. y-Achse entfernt ist.
Zeichnen Sie beispielsweise den Punkt (2, -5) auf der kartesischen Ebene ein. Die Analyse des Vorzeichens der Koordinaten zeigt, dass der Punkt im 4. Quadranten liegt. Es ist 2 Einheiten von der x-Achse (nach rechts) und 5 Einheiten von der y-Achse (unten) entfernt, wobei der Ursprung als Referenzpunkt dient.
Trigonometrische Werte in verschiedenen Quadranten
Die Werte verschiedener trigonometrische Funktionen in verschiedenen Quadranten können durch das Studium der unten hinzugefügten Tabelle gelernt werden, da:
| Quadrant | Ohne | Cos | Also | Kosekans | Sekante | Kotangens |
|---|---|---|---|---|---|---|
| 1. Quadrant | + | + | + | + | + | + |
| 2. Quadrant | + | – | + Pyspark-Tutorial | + | – | – |
| 3. Quadrant | – | – | – | – | – | + |
| 4. Quadrant Turbo C++ herunterladen | – | – | – | – | + | – |
Im 1. Quadranten sind alle trigonometrischen Verhältnisse positiv. Im 2. Quadranten sind Sinus und Kosekant positiv (+), während Kosinus und Sekante negativ (-) sind. Im 3. Quadranten sind Tangens und Kotangens positiv (+), während Kosinus und Sekante negativ sind (-). Im 4. Quadranten sind Sinus und Kosekans negativ (-), während Kosinus und Sekante positiv (+) sind.
Mehr lesen,
- Koordinatengeometrie
- Parallele Linien
- Distanzformel
Gelöste Beispiele auf Quadrant
Beispiel 1: Zeichnen Sie den Punkt A (3, -4) ein und identifizieren Sie seinen Quadranten.
Lösung:
Punkt A liegt an den Koordinaten (3, -4). Da die x-Koordinate positiv (3) und die y-Koordinate negativ (-4) ist, liegt Punkt A im Quadranten IV.
Beispiel 2: Zeichnen Sie den Punkt P (-5, 2) ein und bestimmen Sie seinen Quadranten
Lösung:
Die Koordinaten von Punkt P sind (-5, 2). Um den Quadranten zu bestimmen, untersuchen wir die Vorzeichen der x- und y-Koordinaten.
Die X-Koordinate ist -5 und gibt eine Position links vom Ursprung an.
Die Y-Koordinate ist 2 und gibt eine Position über dem Ursprung an.
Da die x-Koordinate negativ und die y-Koordinate positiv ist, liegt Punkt P im Quadranten II.
Punkt P (-5, 2) liegt im Quadranten II der kartesischen Ebene.
Üben Sie Aufgaben zu Quadranten
Problem 1: Zeichnen Sie den Punkt (1, -1) ein und identifizieren Sie seinen Quadranten.
Problem 2: Suchen Sie drei Punkte auf der x-Achse und bestimmen Sie deren Quadranten.
Problem 3: Wenn ein Punkt auf der y-Achse mit den Koordinaten (0, -3) liegt, in welchem Quadranten befindet er sich?
Problem 4: Suchen Sie die Punkte Q (2, 2), R (-2, -2) und S (0, 0) und prüfen Sie auf Kollinearität.
Problem 5: Zeichnen Sie den Punkt (-4, -3) ein und erklären Sie, in welchem Quadranten er liegt.
FAQs zu Quadranten
1. Was ist ein Quadrant in der Mathematik?
In der Mathematik ist ein Quadrant einer der vier Abschnitte, die durch den Schnittpunkt zweier senkrechter Linien oder Achsen entstehen. Diese Achsen werden in einem kartesischen Koordinatensystem normalerweise als x-Achse und y-Achse bezeichnet.
2. Wie nennt man den Schnittpunkt zweier Achsen?
Der Schnittpunkt zweier Achsen in einem kartesischen Koordinatensystem wird als Ursprung bezeichnet. Es wird durch den Punkt dargestellt, an dem sich die x-Achse und die y-Achse treffen, normalerweise als (0,0) bezeichnet.
3. Was sind 4 Quadranten?
Die vier Quadranten sind die Abschnitte, die durch die Unterteilung einer kartesischen Koordinatenebene in vier gleiche Teile gebildet werden. Sie werden als erster Quadrant (Q1), zweiter Quadrant (Q2), dritter Quadrant (Q3) und vierter Quadrant (Q4) bezeichnet.
4. Welcher Quadrant ist positiv?
Der positive Quadrant in einem kartesischen Koordinatensystem ist der erste Quadrant (Q1). In diesem Quadranten sind sowohl die x- als auch die y-Koordinaten positiv.
5. Wozu dienen Quadranten in Diagrammen?
Quadranten in Diagrammen bieten eine systematische Möglichkeit, Punkte anhand ihrer Koordinaten zu organisieren und zu lokalisieren. Sie helfen bei der Visualisierung von Beziehungen zwischen Variablen und der Analyse von Mustern in Datensätzen und erleichtern so die Interpretation grafischer Darstellungen.
6. Welcher Quadrant hat beide Werte für positive Koordinaten?
Der erste Quadrant (Q1) ist der Quadrant, in dem sowohl die x- als auch die y-Koordinaten der Punkte positiv sind. Es ist der einzige Quadrant mit beiden positiven Werten.
7. Was sind die 4 Quadranten eines Kreises?
Das Konzept der Quadranten ist nicht direkt auf Kreise anwendbar. Stattdessen werden Kreise in Winkel unterteilt, die in Grad gemessen werden. Wenn man sich jedoch auf kreisförmige Sektoren bezieht, könnte man Begriffe wie erster Sektor, zweiter Sektor, dritter Sektor und vierter Sektor verwenden, die verschiedenen Winkelbereichen entsprechen.
