Die relationale Algebra ist eine prozedurale Abfragesprache. Es gibt einen schrittweisen Prozess, um das Ergebnis der Abfrage zu erhalten. Es verwendet Operatoren, um Abfragen durchzuführen.
Arten relationaler Operationen
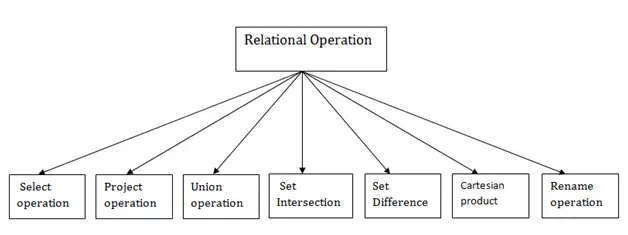
1. Wählen Sie den Vorgang aus:
- Die Auswahloperation wählt Tupel aus, die ein bestimmtes Prädikat erfüllen.
- Es wird mit Sigma (σ) bezeichnet.
Notation: σ p(r)
Wo:
P wird zur Auswahlvorhersage verwendet
R wird für die Relation verwendet
P wird als aussagenlogische Formel verwendet, die Konnektoren wie AND OR und NOT verwenden kann. Diese Relationen können als relationale Operatoren wie =, ≠, ≧, , ≦ verwendet werden.
Beispiel: LOAN-Beziehung
| ZWEIGNAME | LOAN_NO | MENGE |
|---|---|---|
| Innenstadt | L-17 | 1000 |
| Redwood | L-23 | 2000 |
| Perryride | L-15 | 1500 |
| Innenstadt | L-14 | 1500 |
| Mianus | L-13 | 500 |
| Roundhill | L-11 | 900 |
| Perryride | L-16 | 1300 |
Eingang:
σ BRANCH_NAME='perryride' (LOAN)
Ausgabe:
Matrixmultiplikation in c
| ZWEIGNAME | LOAN_NO | MENGE |
|---|---|---|
| Perryride | L-15 | 1500 |
| Perryride | L-16 | 1300 |
2. Projektbetrieb:
- Diese Operation zeigt die Liste der Attribute an, die im Ergebnis erscheinen sollen. Die restlichen Attribute werden aus der Tabelle entfernt.
- Es wird mit ∏ bezeichnet.
Notation: ∏ A1, A2, An (r)
Wo
A1 , A2 , A3 wird als Attributname einer Beziehung verwendet R .
Beispiel: KUNDENBEZIEHUNG
Nick Pulos schwarzer Blitz
| NAME | STRASSE | STADT |
|---|---|---|
| Jones | Hauptsächlich | Harrison |
| Schmied | Norden | Roggen |
| Heu | Hauptsächlich | Harrison |
| Curry | Norden | Roggen |
| Johnson | Seele | Brooklyn |
| Brooks | Senator | Brooklyn |
Eingang:
∏ NAME, CITY (CUSTOMER)
Ausgabe:
| NAME | STADT |
|---|---|
| Jones | Harrison |
| Schmied | Roggen |
| Heu | Harrison |
| Curry | Roggen |
| Johnson | Brooklyn |
| Brooks | Brooklyn |
3. Gewerkschaftsoperation:
- Angenommen, es gibt zwei Tupel R und S. Die Vereinigungsoperation enthält alle Tupel, die entweder in R oder S oder beide in R & S sind.
- Es eliminiert die doppelten Tupel. Es wird mit ∪ bezeichnet.
Notation: R ∪ S
Eine Union-Operation muss die folgende Bedingung erfüllen:
- R und S müssen das Attribut der gleichen Zahl haben.
- Doppelte Tupel werden automatisch entfernt.
Beispiel:
EINLAGERBEZIEHUNG
| KUNDENNAME | KONTO NR |
|---|---|
| Johnson | A-101 |
| Schmied | A-121 |
| Mayes | A-321 |
| Turner | A-176 |
| Johnson | A-273 |
| Jones | A-472 |
| Lindsay | A-284 |
LEIHEBEZIEHUNG
| KUNDENNAME | LOAN_NO |
|---|---|
| Jones | L-17 |
| Schmied | L-23 |
| Hayes | L-15 |
| Jackson | L-14 |
| Curry | L-93 |
| Schmied | L-11 |
| Williams | L-17 |
Eingang:
Beispiele für Javascript-Beispielcode
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
Ausgabe:
| KUNDENNAME |
|---|
| Johnson |
| Schmied |
| Hayes |
| Turner |
| Jones |
| Lindsay |
| Jackson |
| Curry |
| Williams |
| Mayes |
4. Schnittpunkt festlegen:
- Angenommen, es gibt zwei Tupel R und S. Die Schnittmengenoperation enthält alle Tupel, die sich sowohl in R als auch in S befinden.
- Es wird mit dem Schnittpunkt ∩ bezeichnet.
Notation: R ∩ S
Beispiel: Verwendung der oben genannten DEPOSITOR-Tabelle und BORROW-Tabelle
Eingang:
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
Ausgabe:
| KUNDENNAME |
|---|
| Schmied |
| Jones |
5. Differenz einstellen:
- Angenommen, es gibt zwei Tupel R und S. Die Schnittmengenoperation enthält alle Tupel, die in R, aber nicht in S liegen.
- Es wird durch Schnittpunkt minus (-) bezeichnet.
Notation: R - S
Beispiel: Verwendung der oben genannten DEPOSITOR-Tabelle und BORROW-Tabelle
Eingang:
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
Ausgabe:
Objekt von Java
| KUNDENNAME |
|---|
| Jackson |
| Hayes |
| Williams |
| Curry |
6. Kartesisches Produkt
- Das kartesische Produkt wird verwendet, um jede Zeile in einer Tabelle mit jeder Zeile in der anderen Tabelle zu kombinieren. Es wird auch als Kreuzprodukt bezeichnet.
- Es wird mit X bezeichnet.
Notation: E X D
Beispiel:
MITARBEITER
| EMP_ID | EMP_NAME | EMP_DEPT |
|---|---|---|
| 1 | Schmied | A |
| 2 | Harry | C |
| 3 | John | B |
ABTEILUNG
| DEPT_NO | DEPT_NAME |
|---|---|
| A | Marketing |
| B | Verkäufe |
| C | Legal |
Eingang:
EMPLOYEE X DEPARTMENT
Ausgabe:
| EMP_ID | EMP_NAME | EMP_DEPT | DEPT_NO | DEPT_NAME |
|---|---|---|---|---|
| 1 | Schmied | A | A | Marketing |
| 1 | Schmied | A | B | Verkäufe |
| 1 | Schmied | A | C | Legal |
| 2 | Harry | C | A | Marketing |
| 2 | Harry | C | B | Verkäufe |
| 2 | Harry | C | C | Legal |
| 3 | John | B | A | Marketing |
| 3 | John | B | B | Verkäufe |
| 3 | John | B | C | Legal |
7. Vorgang umbenennen:
Mit der Umbenennungsoperation wird die Ausgabebeziehung umbenannt. Es wird mit bezeichnet rho (P).
Beispiel: Wir können den Umbenennungsoperator verwenden, um die STUDENT-Beziehung in STUDENT1 umzubenennen.
ρ(STUDENT1, STUDENT)
