Sin-Cos-Formeln in der Trigonometrie: Trigonometrie ist, wie der Name schon sagt, die Lehre von Dreiecken. Es ist ein wichtiger Zweig der Mathematik, der die Beziehung zwischen Seitenlängen und Winkeln des rechtwinkligen Dreiecks untersucht und auch bei der Bestimmung der fehlenden Seitenlängen oder Winkel eines Dreiecks hilft. Es gibt sechs trigonometrische Verhältnisse oder Funktionen: Sinus, Kosinus, Tangens, Kosekans, Sekanten und Kotangens, wobei Kosekans, Sekanten und Kotangens die reziproken Funktionen der anderen drei Funktionen sind, d. h. Sinus, Kosinus bzw. Tangens.
Ein trigonometrisches Verhältnis ist definiert als das Verhältnis der Seitenlängen eines rechtwinkligen Dreiecks. Trigonometrie wird in verschiedenen Bereichen unseres täglichen Lebens eingesetzt. Es hilft, die Höhe von Hügeln oder Gebäuden zu bestimmen. Es wird auch in Bereichen wie Kriminologie, Bauwesen, Physik, Archäologie, Schiffsmotorenbau usw. verwendet.
In diesem Artikel werden wir alles untersuchen Trigonometrieformeln, hauptsächlich Sinus- und Kosinusformeln mit ihren Beispielen und eine Liste aller Formeln in der Trigonometrie.
Inhaltsverzeichnis
- Formeln in der Trigonometrie
- Einige grundlegende Sin-Cos-Formeln
- Tabelle der Sin-Cos-Formeln
- Beispiele für Sin-Cos-Formeln
- Üben Sie Probleme zu Sin-Cos-Formeln in der Trigonometrie anhand von Beispielen
Formeln in der Trigonometrie
Betrachten wir ein rechtwinkliges Dreieck XYZ, wobei ∠Y = 90°. Der Winkel am Scheitelpunkt Z sei θ. Die zu θ benachbarte Seite wird als angrenzende Seite bezeichnet, und die zu θ gegenüberliegende Seite wird als Gegenseite bezeichnet. Eine Hypotenuse ist eine dem rechten Winkel gegenüberliegende Seite oder die längste Seite eines rechten Winkels.
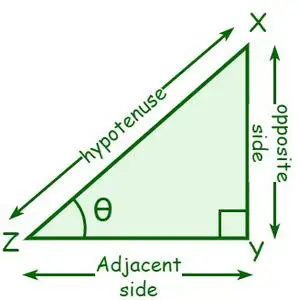
- sin θ = Opposite side/Hypotenuse
- cos θ = Ankathete/Hypotenuse
- tan θ = Gegenseite/Angrenzende Seite
- cosec θ = 1/sin θ = Hypotenuse/Gegenkathete
- sec θ = 1/ cos θ = Hypotenuse/Ankathete
- cot θ = 1/ tan θ = Angrenzende Seite/Gegenseite
Sinusformel
Der Sinus eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der gegenüberliegenden Seite zur Länge der Hypotenuse zum gegebenen Winkel. Eine Sinusfunktion wird als Sünde dargestellt.
sin θ = Opposite side/Hypotenuse
Kosinusformel
Der Kosinus eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der Ankathete zur Länge der Hypotenuse zum gegebenen Winkel. Eine Kosinusfunktion wird als cos dargestellt.
Wann kam Win 7 heraus?cos θ = Ankathete/Hypotenuse
Einige grundlegende Sin-Cos-Formeln
Sinus- und Kosinusfunktionen in Quadranten
- Die Sinusfunktion ist im ersten und zweiten Quadranten positiv und im dritten und vierten Quadranten negativ.
- Die Kosinusfunktion ist im ersten und vierten Quadranten positiv und im zweiten und dritten Quadranten negativ.
Abschlüsse
Quadrant
Vorzeichen der Sinusfunktion
Vorzeichen der Kosinusfunktion
0° bis 90°
1. Quadrant
+ (positiv)
+ (positiv)
90° bis 180°
2. Quadrant
+ (positiv)
– (negativ)
180° bis 270°
3. Quadrant
– (negativ)
– (negativ)
270° bis 360°
4. Quadrant
– (negativ)
+ (positiv)
Die negative Winkelidentität der Sinus- und Kosinusfunktionen
- Der Sinus eines negativen Winkels ist immer gleich dem negativen Sinus des Winkels.
Sünde (– θ) = – Sünde θ
- Der Kosinus eines negativen Winkels ist immer gleich dem Kosinus des Winkels.
cos (– θ) = cos θ
Zusammenhang zwischen Sinus- und Kosinusfunktion
sin θ = cos (90° – θ)
Reziproke Funktionen der Sinus- und Kosinusfunktionen
- Eine Kosekansfunktion ist die Kehrfunktion der Sinusfunktion.
cosec θ = 1/sin θ
- Eine Sekantenfunktion ist die Kehrfunktion der Kosinusfunktion.
Sek. θ = 1/cos θ
Pythagoräische Identität
ohne 2 θ + cos 2 θ = 1
Periodische Identitäten der Sinus- und Kosinusfunktionen
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Doppelwinkelformeln für die Sinus- und Kosinusfunktionen
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – Sünde 2 θ = 2 cos 2 θ – 1 = 1 – 2 Sünde 2 ich
Halbwinkelidentitäten für die Sinus- und Kosinusfunktionen
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Dreifache Winkelidentitäten für die Sinus- und Kosinusfunktionen
Sünde 3θ = 3 Sünde θ – 4 Sünde 3 ich
cos 3θ = 4cos 3 θ – 3 cos θ
Summen- und Differenzformeln
- Sinusfunktion
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- Kosinusfunktion
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Sinusgesetz oder Sinusregel
Das Sinusgesetz ist ein trigonometrisches Gesetz, das eine Beziehung zwischen den Seitenlängen und Winkeln eines Dreiecks angibt.

a/sin A = b/sin B = c/sin C
Dabei sind a, b und c die Längen der drei Seiten des Dreiecks ABC und A, B und C die Winkel.
Kosinusgesetz
Zur Bestimmung der fehlenden oder unbekannten Winkel oder Seitenlängen eines Dreiecks wird das Kosinusgesetz verwendet.

A 2 = b 2 + c 2 – 2vc cos A
B 2 = c 2 + a 2 – 2ca cos B
C 2 = a 2 + b 2 – 2ab cos C
Dabei sind a, b und c die Längen der drei Seiten des Dreiecks ABC und A, B und C die Winkel.
Tabelle der Sin-Cos-Formeln
Hier ist die Tabelle/Liste der Sin- und Cos-Formeln für verschiedene Winkel in Grad und im Bogenmaß:
Liste der Sin-Cos-Formeln
| Winkel (in Grad) | Winkel (im Bogenmaß) | Sünde ich | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | S. 6 | 1/2 | _3/2 |
| 45° | S./4 | 1/√2 | 1/√2 |
| 60° | S./3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Beispiele für Sin-Cos-Formeln
Aufgabe 1: Wenn cos α = 24/25, dann ermitteln Sie den Wert von sin α.
Lösung:
Gegeben,
cos α = 24/25
Von den pythagoreischen Identitäten haben wir;
cos2θ + Sünde2θ = 1
(24/25)2+ ohne2α = 1
ohne2α = 1 – (24/25)2
ohne2α = 1 – (576/625) = (625 – 576)/625
ohne2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Daher ist sin α = ±7/25.
Aufgabe 2: Beweisen Sie die sin 2A- und cos 2A-Formeln, wenn ∠A= 30°.
Lösung:
Gegeben sei ∠A= 30°
Wir wissen das,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Da sin 30° = 1/2, cos 30° = √3/2 und sin 60° = √3/2}
√3/2 = √3/2
L.H.S. = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Da cos 60° = 1/2 und cos 30° = √3/2}
1/2 = 1/2
L.H.S. = R.H.S
Somit bewiesen.
Aufgabe 3: Finden Sie den Wert von cos x, wenn tan x = 3/4.
Lösung:
Gegeben sei tan x = 3/4
Wir wissen das,
tan x = gegenüberliegende Seite/angrenzende Seite = 3/4
Um die Hypotenuse zu finden, verwenden wir den Satz des Pythagoras:
Hypotenuse2= Gegenteil2+ angrenzend2
H2= 32+ 42
H2= 9 + 16 = 25
Java konvertiert int in einen StringH = √25 = 5
Nun ist cos x = Ankathete/Hypotenuse
cos x = 4/5
Somit beträgt der Wert von cos x 4/5.
Aufgabe 4: Finden Sie ∠C (in Grad) und ∠A (in Grad), wenn ∠B = 45°, BC = 15 Zoll und AC = 12 Zoll.

Lösung:
Gegeben: ∠B = 45°, BC = a = 15 Zoll und AC = b = 12 Zoll.
Aus dem Sinusgesetz haben wir
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ sin A = 15/16,97 = 0,8839
⇒ ∠A = Sünde-1(0,8839) = 62,11°
Wir wissen, dass die Summe der Innenwinkel eines Dreiecks 180° beträgt.
Also, ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Daher ist ∠A = 62,11° und ∠C = 72,89°.
Aufgabe 5: Beweisen Sie Halbwinkelidentitäten der Kosinusfunktion.
Lösung:
Die Halbwinkelidentität der Kosinusfunktion ist:
cos (θ/2) = ±√[(1 + cos θ)/2]
Aus Doppelwinkelidentitäten haben wir:
cos 2A = 2 cos2A – 1
Ersetzen Sie nun A auf beiden Seiten durch θ/2
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Somit bewiesen.
Üben Sie Probleme zu Sin-Cos-Formeln in der Trigonometrie anhand von Beispielen
1. Gegeben sei sin θ = 3/5. Finden Sie cos θ.
2. Beweisen Sie die Identität sin(2A) = 2 sinA cosA für A=45∘.
3. Wenn cos α = 5/13. Finden Sie Sünde(2a).
4. Lösen Sie nach θ auf, wenn sin θ = cos(90∘−θ).
5. Wenn tan β = 2. Finden Sie sin β und cos β mithilfe der pythagoräischen Identität.
FAQs zu Sin-Cos-Formeln in der Trigonometrie mit Beispielen
Was sind die grundlegenden Sinus- und Cosinusformeln in der Trigonometrie?
Die grundlegenden Sinus- und Kosinusformeln sind sin θ = Gegenkathete/Hypotenuse und cos θ = Ankathete/Hypotenuse, wobei θ ein Winkel in einem rechtwinkligen Dreieck ist.
Wie ermittelt man Sinus und Cosinus spezieller Winkel?
Spezielle Winkel wie 0∘, 30∘, 45∘, 60∘ und 90∘ haben spezifische Sinus- und Kosinuswerte, die mithilfe trigonometrischer Tabellen oder Einheitskreiskonzepten gespeichert werden können.
Welche Beziehung besteht zwischen Sinus- und Cosinusfunktionen?
Die Sinus- und Kosinusfunktionen hängen durch die Identität zusammen sin θ = cos(90∘- θ) und die pythagoreische Identität ohne 2 θ+cos 2 θ = 1.
Wie verwendet man die Doppelwinkelformeln für Sinus und Cosinus?
Die Doppelwinkelformeln lauten sin(2θ) = 2sinθcosθ Und cos(2θ)=cos 2 θ – sin 2 ich. Diese werden verwendet, um trigonometrische Funktionen von Doppelwinkeln als Einzelwinkel auszudrücken.
Wie finden Sie die Werte von Sinus und Cosinus für Winkel in verschiedenen Quadranten?
Die Vorzeichen von Sinus- und Cosinusfunktionen hängen davon ab, in welchem Quadranten der Winkel liegt:
- Erster Quadrant: sin θ> 0 und cos θ> 0
- Zweiter Quadrant: sin θ> 0 und cos θ <0
- Dritter Quadrant: sinθ <0 und cosθ < 0
- Vierter Quadrant: sinθ 0
