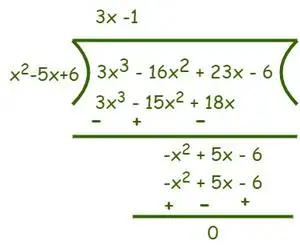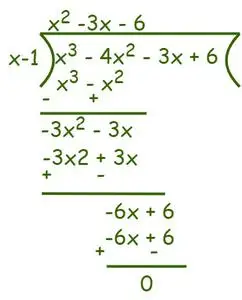Kubische Gleichung ist eine mathematische Gleichung, in der ein Polynom vom Grad 3 einer Konstante oder einem anderen Polynom vom höchsten Grad 2 gleichgesetzt wird. Die Standarddarstellung der kubischen Gleichung ist Axt ³ +bx ² +cx+d = 0 wobei a, b, c und d reelle Zahlen sind. Einige Beispiele für kubische Gleichungen sind X ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 usw.

Inhaltsverzeichnis

• Polynomdefinition
• Grad der Gleichung
• Kubische Gleichungsdefinition
• Wie löst man kubische Gleichungen?
• Kubische Gleichungen lösen
• Kubische Gleichung mithilfe von Faktoren lösen
• Kubische Gleichung mit grafischer Methode lösen
• Probleme basierend auf der Lösung kubischer Gleichungen
• Üben Sie Aufgaben zur Lösung kubischer Gleichungen

Um zu lernen, wie man kubische Gleichungen löst, müssen wir zunächst etwas über Polynome, den Grad des Polynoms und andere Dinge lernen. In diesem Artikel erfahren Sie mehr über Polynome, Polynomgleichungen, das Lösen kubischer Gleichungen oder wie man kubische Gleichungen löst und vieles mehr im Detail.

Polynomdefinition

Polynom ist wie folgt definiert:

A Polynom ist ein algebraischer Ausdruck, bei dem die Potenz einer Variablen eine nichtnegative ganze Zahl ist. Die allgemeine Form eines Polynoms ist a₀X^N+ a₁X^n-1+ a₂X^n-2+… + a_N. Abhängig von der maximalen Potenz der Variablen kann ein Polynom als Monom, Binomial, Trinom usw. klassifiziert werden.

Was ist eine Gleichung?

Eine Gleichung ist wie folgt definiert:

Eine Gleichung ist ein Polynom, das einem numerischen Wert oder einem anderen Polynom gleichgesetzt wird. Zum Beispiel ist x + 2 ein Polynom, aber x + 2 = 5 ist eine Gleichung. Ebenso ist 2x + 3 = x + 1 ebenfalls eine Gleichung, während 2x + 3 und x + 1 einzeln Polynome sind.

Grad der Gleichung

Die Definition des Gleichungsgrads ist unten angegeben:

Grad einer Gleichung ist definiert als die maximale Leistung, die die Variable in einer Gleichung besitzt.

Basierend auf dem Grad der Gleichung kann eine Gleichung wie folgt klassifiziert werden:

• Lineare Gleichung
• Quadratische Gleichung
• Kubische Gleichung
• Biquadratische Gleichung

Lineare Gleichung

Die Gleichung, in der die maximale Potenz der Variablen 1 ist, wird als lineare Gleichung bezeichnet.

• Zum Beispiel 3x +1 = 0

Quadratisches Polynom

Die Gleichung, in der die maximale Potenz der Variablen 2 beträgt, ist eine quadratische Gleichung.

• Zum Beispiel 3x²+x+1 = 0

Kubische Gleichung

Die Gleichung, in der die maximale Potenz der Variablen 3 beträgt, wird als kubische Gleichung bezeichnet.

• Zum Beispiel 5x³+3x²+x+1 = 0

Biquadratisches Polynom

Die Gleichung, in der die maximale Potenz der Variablen 4 beträgt, wird biquadratisches Polynom oder quartisches Polynom genannt.

• Zum Beispiel 5x⁴+4x³+3x²+2x+1 = 0

Kubische Gleichungsdefinition

Kubische Gleichung ist eine algebraische Gleichung, bei der der höchste Grad des Polynoms 3 ist. Einige Beispiele für kubische Gleichungen sind 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 usw.

Die allgemeine Form einer kubischen Gleichung ist:

Axt ³ + bx ² + cx + d = 0, a ≠ 0

Wo,

• a, b, Und C sind die Koeffizienten der Variablen und ihre Exponenten und D ist die Konstante, und
• a, b, c Und D sind reelle Zahlen.

Wie löst man kubische Gleichungen?

Eine kubische Gleichung ist eine Gleichung mit Grad drei. Es gibt drei Lösungen und kann leicht gelöst werden, indem Sie die unten hinzugefügten Schritte befolgen:

Schritt 1: Finden Sie eine Lösung der kubischen Gleichung mit der Hit-and-Try-Methode. Angenommen, wir haben eine kubische Gleichung P(x), dann finden Sie für jedes x = a P(a) = 0, indem Sie x = 0, ±1, ±2, ±3, … usw. nehmen.

Schritt 2: Wenn wir P(a) = 0 erhalten, ermitteln Sie den Faktor (x – a) von P(x).

Schritt 3: Teilen Sie P(x) durch (x – a), um mithilfe einer Polynomdivision eine quadratische Gleichung, beispielsweise Q(x), zu erhalten.

Schritt 4: Faktarisieren Sie die quadratische Gleichung Q(x), um die Faktoren (x – b) und (x – c) zu erhalten.

Schritt 5: (x – a), (x – b) und (x – c) sind die Faktoren von P(x) und wenn wir jeden Faktor lösen, erhalten wir die Wurzeln der Gleichung als a, b und c.

Lerne mehr über, Divisionspolynom

Kubische Gleichungen lösen

A Kubische Gleichung kann mit zwei Methoden gelöst werden

• Indem man es in eine quadratische Gleichung reduziert und sie dann entweder durch Faktorisieren oder die quadratische Formel löst
• Nach grafischer Methode

A Kubische Gleichung hat drei Wurzeln. Diese Wurzeln können real oder imaginär sein. Es kann auch unterschiedliche Wurzeln oder zwei gleiche und eine unterschiedliche Wurzel und alle drei gleichen Wurzeln geben.

Es ist zu beachten, dass für jede Gleichung, einschließlich Kubische Gleichungen , muss die Gleichung immer zuerst in ihrer Standardform arrangiert werden, bevor die Gleichung gelöst wird.

Zum Beispiel, wenn die gegebene Gleichung 2x ist²-5 = x + 4/x, dann müssen wir dies in seine Standardform umordnen, d. h. 2x³-X²-5x-4 = 0. Jetzt können wir die Gleichung mit jeder geeigneten Methode lösen.

Kubische Gleichung mithilfe von Faktoren lösen

Die Lösung der kubischen Gleichung mithilfe des Faktorsatzes wird anhand des unten hinzugefügten Beispiels erläutert:

Beispiel: Finden Sie die Wurzeln der Gleichung f(x) = 3x ³ −16x ² + 23x − 6 = 0.

Lösung:

Gegebener Ausdruck: f(x) = 3x³−16x²+ 23x − 6 = 0

Zerlegen Sie zunächst das Polynom, um Wurzeln zu erhalten

Da die Konstante -6 ist, sind die möglichen Faktoren 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Wir wissen das, laut Faktorsatz Wenn f(a) = 0, dann ist (x-a) ein Faktor von f(x)

Also sind (x – 2) und (x – 3) Faktoren von f(x). Daher ist das Produkt aus (x – 2) und (x – 3) auch der Faktor von f(x). Um nun die verbleibenden Faktoren zu ermitteln, verwenden Sie die Methode der langen Division und dividieren Sie f(x) durch das Produkt von (x – 2) und (x – 3).

Daher ist Teiler = (x – 2)(x – 3) = (x²– 5x + 6) und Dividende = 3x³−16x²+ 23x − 6. Teilen Sie nun wie unten gezeigt:

Nach der Division erhalten wir (3x-1) als Quotienten und der Rest ist 0. Nun gemäß Divisionsalgorithmus Wir wissen das Dividende = Divisor×Quotient+Rest.

⇒ f(x) = (3x³−16x²+ 23x − 6) = (x²– 5x + 6)(3x-1)

Da f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒ x²– 5x + 6 = 0 oder 3x-1 = 0

Jetzt nehmen wir 3x-1 = 0 ⇒ x = 1/3, da wir bereits zwei Wurzeln aus x kennen²– 5x + 6, also 2 und 3

Also,

Wurzeln des Gegebenen Kubische Gleichung sind 1/3, 2 und 3.

Kubische Gleichung mit grafischer Methode lösen

Eine kubische Gleichung wird grafisch gelöst, wenn Sie die gegebene Gleichung nicht mit anderen Techniken lösen können. Wir benötigen also eine genaue Zeichnung der gegebenen kubischen Gleichung. Die Wurzeln der Gleichung sind die Punkte, an denen der Graph die schneidet die Y-Achse.

Die Anzahl der reellen Lösungen der kubischen Gleichung ist gleich der Häufigkeit, mit der der Graph der kubischen Gleichung die X-Achse kreuzt.

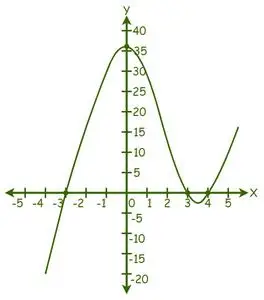
Beispiel: Finden Sie die Wurzeln der Gleichung f(x) = x ³ − 4x ² − 9x + 36 = 0, mit der grafischen Methode.

Lösung:

Gegebener Ausdruck: f(x) = x³− 4x²− 9x + 36 = 0.

Ersetzen Sie nun einfach zufällige Werte für x im Diagramm für die gegebene Funktion:

X	-4	-3	-2 Sortieralgorithmus für Einfügungen	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

Wir können sehen, dass der Graph die X-Achse an 3 Punkten schneidet, daher gibt es 3 reale Lösungen.

Aus der Grafik ergeben sich folgende Lösungen: x = -3, x = 3 und x = 4.

Daher sind die Wurzeln der gegebenen Gleichung -3, 3 und 4.

Mehr lesen,

• Lineare Gleichung
• Quadratische Gleichung lösen
• Faktorisierung von Polynomen

Probleme basierend auf der Lösung kubischer Gleichungen

Aufgabe 1: Finden Sie die Wurzeln von f(x) = x ³ – 4x ² -3x + 6 = 0.

Lösung:

Gegebener Ausdruck: f(x) = x³– 4x²-3x + 6 = 0.

Zerlegen Sie zunächst das Polynom, um Wurzeln zu erhalten.

Da die Konstante +6 ist, sind die möglichen Faktoren 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Also, laut Faktorsatz (x – 1) ist ein Faktor der gegebenen Gleichung. Um nun die verbleibenden Faktoren zu ermitteln, verwenden Sie die Methode der langen Division.

Entsprechend Divisionsalgorithmus wir können schreiben,

Also ist f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 oder (x²– 3x – 6) = 0

Wir wissen, dass die Wurzeln einer quadratischen Gleichung ax sind²+ bx + c = 0 sind,

x = [-b ± √(b²-4ac)]/2a

Daher ist für (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Daher sind die Wurzeln der gegebenen kubischen Gleichung 1, (3+√33)/2 und (3–√33)/2.

Aufgabe 2: Finden Sie die Wurzeln der Gleichung f(x) = 4x ³ – 10x ² + 4x = 0.

Lösung:

Gegebener Ausdruck: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 oder 4x – 2 = 0, x – 2 = 0

⇒ x = 0 oder x = 1/2 oder x = 2

Daher sind die Wurzeln der gegebenen Gleichung 0, 1/2 und 2.

Aufgabe 3: Finden Sie die Wurzeln der Gleichung f(x) = x ³ + 3x ² + x + 3 = 0.

Lösung:

Gegebener Ausdruck: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 oder x²+1 = 0

⇒ x = -3, ±i

Die gegebene Gleichung hat also eine reelle Wurzel, d. h. -3, und zwei imaginäre Wurzeln, d. h. ±i.

Aufgabe 4: Finden Sie die Wurzeln der Gleichung f(x) = x ³ – 7x ² – x + 7 = 0.

Lösung:

Gegebene Ausdrücke,

f(x) = x³– 3x²– 5x + 7 = 0

Faktorisieren Sie zunächst die Gleichung f(x): x³– 3x²– 5x + 7= 0

Es kann zu (x-7)(x+1)(x-1) = 0 faktorisiert werden

Nachdem wir das Polynom faktorisiert haben, können wir die Wurzeln finden, indem wir jeden Faktor mit Null gleichsetzen. Zum Beispiel:

• x – 7 = 0, also x = 7
• x + 1 = 0, also x = -1
• x – 1 = 0, also x = 1

Also sind die Wurzeln der Gleichung f(x): x³– 3x²– 5x + 7 = 0 sind

• x = 7
• x = -1
• x = 1

Aufgabe 5: Finden Sie die Wurzeln der Gleichung f(x) = x ³ − 6x ² + 11x − 6 = 0, mit der grafischen Methode.

Lösung:

Gegebener Ausdruck: f(x) = x³− 6x²+ 11x − 6 = 0.

Ersetzen Sie nun einfach zufällige Werte für x im Diagramm für die gegebene Funktion:

X	1	2	3	4	5
f(x)	0	0	0	6	24

Wir können sehen, dass der Graph die X-Achse an 3 Punkten schneidet, daher gibt es 3 reale Lösungen.

Aus dem Diagramm ergeben sich folgende Lösungen: x = 1, x = 2 und x = 3.

Daher sind die Wurzeln der gegebenen Gleichung 1, 2 und 3.

Üben Sie Aufgaben zur Lösung kubischer Gleichungen

Im Folgenden werden verschiedene Übungsaufgaben im Zusammenhang mit kubischen Gleichungen hinzugefügt. Lösen Sie diese Probleme, um das Konzept „Wie löst man eine kubische Gleichung?“ vollständig zu verstehen.

P1. Lösen Sie die kubische Gleichung 3x³+ 2x²– 11x + 7 = 0.

P2. Finden Sie die Wurzeln der kubischen Gleichung, 4x³– 12x²+ 17 = 0.

P3. Lösen Sie die kubische Gleichung x³+ 4x²– x + 3 = 0 mit grafischer Methode.

P4. Finden Sie die Zahl, die -9x erfüllt³+ 11x²– 8x + 2 = 0.

FAQs zum Lösen kubischer Gleichungen

1. Was sind kubische Gleichungen?

Kubische Gleichungen sind algebraische Gleichungen, in denen die maximale Potenz einer Variablen 3 beträgt

2. Wie faktorisiert man eine kubische Gleichung?

Wir können eine kubische Gleichung auf zwei Arten faktorisieren. Indem wir zunächst einen gemeinsamen linearen Ausdruck aus der gegebenen kubischen Gleichung nehmen, erhalten wir einen linearen und einen quadratischen Ausdruck als Produkt. Diese quadratische Gleichung kann weiter faktorisiert werden, um alle Faktoren zu erhalten. Die zweite Methode besteht darin, durch Eingabe zufälliger Werte eine Nullstelle der gegebenen kubischen Gleichung zu finden. Der Wert, für den wir den Wert der Gleichung auf Null setzen, ist eine der Nullstellen der gegebenen kubischen Gleichung. Bilden Sie nun mithilfe des Faktorsatzes einen linearen Ausdruck, sagen wir x-a, und dividieren Sie die gegebene kubische Gleichung durch diesen Ausdruck, wodurch eine quadratische Gleichung als Quotient entsteht. Diese erhaltene quadratische Gleichung kann weiter faktorisiert werden, um alle Faktoren zu erhalten.

3. Wie löst man eine kubische Gleichung grafisch?

Um eine kubische Gleichung grafisch zu lösen, geben Sie zufällige Werte für x in die gegebene kubische Gleichung ein und lösen Sie sie. Sie erhalten die Werte von y. Tragen Sie diese erhaltenen Werte in die Grafik ein. Finden Sie die Koordinaten, an denen der Graph die x-Achse schneidet. Diese Koordinaten sind die Lösung der kubischen Gleichung.

4. Können alle kubischen Gleichungen exakt gelöst werden?

Jede Gleichung mit ungerader Potenz muss eine reelle Wurzel haben. Daher muss eine kubische Gleichung mindestens eine reelle Wurzel haben, im Gegensatz zu einer quadratischen Gleichung, bei der beide Wurzeln imaginär sein können, wenn die Diskriminante kleiner als Null ist.

5. Kann eine kubische Gleichung mehrere Lösungen haben?

Ja, kubische Gleichungen können mehrere Lösungen haben, da eine kubische Gleichung bis zu drei verschiedene reelle Wurzeln haben kann.

6. Was versteht man unter dem Grad einer Gleichung?

Die maximale Potenz einer Variablen in einer Gleichung wird als Grad eines Polynoms bezeichnet.

7. Was ist der Unterschied zwischen einem Polynom und einer Gleichung?

Polynom ist einfach eine algebraische Gleichung, in der die Potenz der Variablen eine nichtnegative ganze Zahl ist. Wenn dieses Polynom mit einem numerischen Wert oder einem anderen Polynom gleichgesetzt (=) wird, wird es als Gleichung bezeichnet.

8. Was ist der Faktorsatz für kubische Gleichungen?

Der Faktorsatz besagt, dass, wenn r eine Wurzel (Lösung) der kubischen Gleichung ax ist³+ bx²+ cx + d = 0, dann ist x – r ein Faktor der Gleichung.

9. Was passiert, wenn ich mithilfe von Formeln keine genauen Lösungen finden kann?

Wenn es unmöglich erscheint, exakte Lösungen zu finden, können wir numerische Methoden wie iterative Methoden (z. B. die Newton-Methode) verwenden, um die Wurzeln der Gleichung anzunähern.

Lerne mehr über Newton Raphsons Methode .