Die Standardform einer Parabel ist y = ax2+ bx + c wobei a, b und c reelle Zahlen sind und a ungleich Null ist. Eine Parabel ist definiert als die Menge aller Punkte in einer Ebene, die den gleichen Abstand von einer festen Linie und einem festen Punkt in der Ebene haben.
In diesem Artikel werden wir im Detail verstehen, was eine Parabel ist, die Standardgleichung einer Parabel, verwandte Beispiele und andere.
Inhaltsverzeichnis
- Was ist eine Parabel?
- Gleichung einer Parabel
- Teile einer Parabel
- Beispiele zur Gleichung einer Parabel
Was ist eine Parabel?
Eine Parabel ist ein Kegelschnitt, der als Menge aller Punkte definiert ist, die den gleichen Abstand von einem Punkt namens Fokus und einer Linie namens Leitlinie haben. Die Standardgleichungen für eine Parabel hängen von ihrer Ausrichtung (Öffnungsrichtung) und Position ab.
Gleichung einer Parabel
Die Parabelgleichung kann in Standardform oder allgemeiner Form geschrieben werden und beide werden unten hinzugefügt:
Allgemeine Gleichungen einer Parabel
Die allgemeine Gleichung einer Parabel lautet:
y = 4a(x – h) 2 + k
(oder)
x = 4a(y – k) 2 + h
Wobei (h, k) der Scheitelpunkt einer Parabel ist.
Standardgleichungen einer Parabel
Die Standardgleichung einer Parabel lautet:
y = Axt 2 + bx + c
(oder)
x = ist 2 + von + c
wobei a niemals Null sein kann.
Teile einer Parabel
Einige wichtige Begriffe und Teile einer Parabel sind:
- Fokus: Der Fokus ist der Fixpunkt einer Parabel.
- Directrix: Die Leitlinie einer Parabel ist die Linie senkrecht zur Achse einer Parabel.
- Schwerpunktakkord: Die Sehne, die durch den Brennpunkt einer Parabel verläuft und die Parabel an zwei verschiedenen Punkten schneidet, wird Brennsehne genannt.
- Brennweite: Die Brennweite ist die Entfernung eines Punktes (x1, Und1) auf der Parabel vom Fokus.
- Rechte Seite: Ein Latus rectum ist eine Brennsehne, die durch den Brennpunkt einer Parabel verläuft und senkrecht zur Achse der Parabel verläuft. Die Länge des Latus rectum beträgt LL‘ = 4a.
- Exzentrizität: Das Verhältnis des Abstands eines Punktes vom Fokus zu seinem Abstand von der Leitlinie wird als Exzentrizität (e) bezeichnet. Für eine Parabel ist die Exzentrizität gleich 1, d. h. e = 1.
Eine Parabel hat vier Standardgleichungen, die auf der Ausrichtung der Parabel und ihrer Achse basieren. Jede Parabel hat eine andere Querachse und eine konjugierte Achse.
| Parabelgleichung | Parabel | Formeln der Parameter einer Parabel |
|---|---|---|
| Und 2 = 4ax | 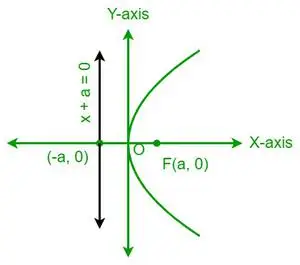 Horizontale Parabel |
|
| Und 2 = -4ax |  Horizontale Parabel |
|
| X 2 = 4 Tage |  Vertikale Parabel |
|
| X 2 = -4ay |  Vertikale Parabel |
|
Im Folgenden sind die Beobachtungen aufgeführt, die anhand der Standardform der Parabelgleichungen gemacht wurden:
- Eine Parabel ist symmetrisch bezüglich ihrer Achse. Zum Beispiel, y2= 4ax ist symmetrisch zur x-Achse, während x2= 4ay ist symmetrisch bezüglich der y-Achse.
- Wenn eine Parabel symmetrisch zur x-Achse ist, dann öffnet sich die Parabel nach rechts, wenn der x-Koeffizient positiv ist, und nach links, wenn der x-Koeffizient negativ ist.
- Wenn eine Parabel symmetrisch zur y-Achse ist, dann öffnet sich die Parabel nach oben, wenn der y-Koeffizient positiv ist, und nach unten, wenn der y-Koeffizient negativ ist.
Im Folgenden sind die Standardgleichungen einer Parabel aufgeführt, wenn die Symmetrieachse entweder parallel zur x-Achse oder zur y-Achse verläuft und der Scheitelpunkt nicht im Ursprung liegt.
| Parabelgleichung | Parabel | Formeln der Parameter einer Parabel |
|---|---|---|
| (und – k)2= 4a(x – h) |  Horizontale Parabel |
|
| (und – k)2= -4a(x – h) |  Horizontale Parabel |
|
| (x – h)2= 4a(y – k) |  Vertikale Parabel |
|
| (x – h)2= -4a(y – k) |  Vertikale Parabel |
|
Gleichung der Parabelableitung
Sei P ein Punkt auf der Parabel, dessen Koordinaten (x, y) sind. Aus der Definition einer Parabel geht hervor, dass der Abstand des Punktes P zum Brennpunkt (F) gleich dem Abstand desselben Punktes P zur Leitlinie einer Parabel ist. Betrachten wir nun einen Punkt X auf der Leitlinie, dessen Koordinaten (-a, y) sind.
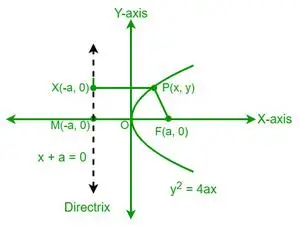
Aus der Definition der Exzentrizität einer Parabel haben wir
e = PF/PX = 1
⇒ PF = PX
Die Koordinaten des Fokus sind (a, 0). Mithilfe der Koordinatenabstandsformel können wir nun den Abstand des Punktes P (x, y) zum Fokus F (a, 0) ermitteln.
PF = √[(x – a)2+ (und – 0)2]
⇒ PF = √[(x – a)2+ und2] ------ (1)
Die Gleichung der Leitlinie lautet x + a = 0. Um den Abstand von PX zu ermitteln, verwenden wir die Formel für den senkrechten Abstand.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
Wir wissen bereits, dass PF = PX. Setzen Sie also die Gleichungen (1) und (2) gleich.
√[(x – a)2+ und2] = (x + a)
Durch Quadrieren auf beiden Seiten erhalten wir:
⇒ [(x – a)2+ und2] = (x + a)2
⇒ x2+ a2– 2ax + y2= x2+ a2+ 2ax
⇒ und2– 2ax = 2ax
⇒ und2= 2ax + 2ax ⇒ Und 2 = 4ax
Damit haben wir die Gleichung einer Parabel abgeleitet. Auf ähnliche Weise können wir die Standardgleichungen der anderen drei Parabeln herleiten.
- Und2= -4ax
- X2= 4 Tage
- X2= -4ay
Und 2 = 4ax, und 2 = -4ax, x 2 = 4ay und x 2 = -4ay sind die Standardgleichungen einer Parabel.
Artikel zum Thema Parabel:
- Kreisgleichung
- Gleichung der Ellipse
- Gleichung der Hyperbel
- Anwendungen der Parabel im wirklichen Leben
Beispiele zur Gleichung einer Parabel
Beispiel 1: Ermitteln Sie die Länge des Latus rectum, des Fokus und des Scheitelpunkts, wenn die Parabelgleichung y ist 2 = 12x.
Lösung:
Gegeben,
Die Parabelgleichung lautet y2= 12x
Durch Vergleich der gegebenen Gleichung mit der Standardform y2= 4ax
4a = 12
⇒ a = 12/4 = 3
Wir wissen das,
Rechte Seite einer Parabel = 4a = 4 (3) = 12
Nun ist der Fokus der Parabel = (a, 0) = (3, 0)
Scheitelpunkt der gegebenen Parabel = (0, 0)
Beispiel 2: Finden Sie die Gleichung der Parabel, die symmetrisch zur X-Achse ist und durch den Punkt (-4, 5) verläuft.
Lösung:
Gegeben,
Die Parabel ist symmetrisch zur X-Achse und hat ihren Scheitelpunkt im Ursprung.
Somit kann die Gleichung die Form y haben2= 4ax oder y2= -4ax, wobei das Vorzeichen davon abhängt, ob sich die Parabel nach links oder rechts öffnet.
Die Parabel muss sich nach links öffnen, da sie durch (-4, 5) verläuft, das im zweiten Quadranten liegt.
Die Gleichung lautet also: y2= -4ax
Setzt man (-4, 5) in die obige Gleichung ein,
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Daher lautet die Gleichung der Parabel: y2= -4(25/16)x (oder) 4y2= -25x.
Beispiel 3: Finden Sie die Koordinaten des Fokus, der Achse, der Geradengleichung und des Latus rectum der Parabel x 2 = 16 Jahre.
Lösung:
Gegeben,
Die Gleichung der Parabel lautet: x2= 16 Jahre
Durch Vergleich der gegebenen Gleichung mit der Standardform x2= 4ay,
4a = 16 ⇒ a = 4
Der Koeffizient von y ist positiv, sodass sich die Parabel nach oben öffnet.
Außerdem liegt die Symmetrieachse entlang der positiven Y-Achse.
Somit,
Der Fokus der Parabel ist (a, 0) = (4, 0).
Die Gleichung der Leitlinie lautet y = -a, d. h. y = -4 oder y + 4 = 0.
Länge des Latus rectum = 4a = 4(4) = 16.
Beispiel 4: Ermitteln Sie die Länge des Latus rectum, des Fokus und des Scheitelpunkts, wenn die Gleichung einer Parabel 2(x-2) ist. 2 + 16 = y.
Lösung:
Gegeben,
Die Gleichung einer Parabel lautet 2(x-2)2+ 16 = und
Durch Vergleich der gegebenen Gleichung mit der allgemeinen Gleichung einer Parabel y = a(x – h)2+ k, wir bekommen
a = 2
(h, k) = (2, 16)
Wir wissen das,
Länge des Latus rectum einer Parabel = 4a
= 4(2) = 8
Nun gilt: Fokus = (a, 0) = (2, 0)
Nun ist Scheitelpunkt = (2, 16)
Beispiel 5: Gleichung einer Parabel ist x 2 – 12x + 4y – 24 = 0, dann finden Sie den Scheitelpunkt, den Fokus und die Leitlinie.
Lösung:
Gegeben,
Die Parabelgleichung lautet x2– 12x + 4y – 24 = 0
⇒ x2– 12x + 36 – 36 + 4y – 24 = 0
⇒ (x – 6)2+ 4 Jahre – 60 = 0
⇒ (x – 6)2= -4(y + 15)
Die erhaltene Gleichung hat die Form (x – h)2= -4a(y – k)
-4a = -4 ⇒ a = 1
Also, der Scheitelpunkt = (h, k) = (6, – 15)
Fokus = (h, k – a) = (6, -15-1) = (6, -16)
Die Gleichung der Leitlinie lautet y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
FAQs zur Parabelgleichung
Wie findet man die Standardgleichung einer Parabel?
Die Standardform der Parabel ist y2= 4ax oder x2= 4 Tage.
Was ist die Normalgleichung der Parabel?
Gleichung der Normalen zur Parabel y2= 4ax mit einer Steigung m ist gegeben als: y = mx – 2 Uhr morgens – morgens 3
Wie findet man den Scheitelpunkt einer Parabel?
Für gegebene Parabel: y = ax2+ bx + c sein Scheitelpunkt kann mit der Formel x = − b/2a ermittelt werden. Setzen Sie diesen x-Wert wieder in die Gleichung ein, um die entsprechende y-Koordinate zu ermitteln.
Gray-Code
