Oberfläche eines Prismas: In der Mathematik ist ein Prisma ein wesentliches Mitglied der Polyederfamilie und wird als eine dreidimensionale Form definiert, die aus zwei identischen, einander zugewandten Polygonen besteht, die seitlich durch rechteckige oder parallelogrammförmige Flächen verbunden sind. Die identischen Polygone können Dreiecke, Quadrate, Rechtecke, Fünfecke oder jedes andere n-seitige Polygon sein und werden als Grundflächen des Prismas bezeichnet. Die anderen Flächen eines Prismas sind Parallelogramme oder Rechtecke.
In diesem Artikel werden wir diskutieren verschiedene Arten von Prismen und die Formel für die Oberfläche von Prismen, mit Beispielen und Übungsaufgaben.
Inhaltsverzeichnis
- Was ist die Oberfläche des Prismas?
- Verschiedene Arten von Prismen
- Formel für die Oberfläche des Prismas
- Beispiele für gelöste Oberfläche eines Prismas
- Übungsaufgaben zur Oberfläche eines Prismas
Was ist die Oberfläche des Prismas?
Als Oberfläche eines Prismas bezeichnet man die Gesamtfläche, die von allen seinen Flächen umschlossen wird. Um die Oberfläche eines Prismas zu bestimmen, müssen wir die Flächen aller seiner Flächen berechnen und dann die resultierenden Flächen addieren. Ein Prisma hat zwei Arten von Oberflächen, nämlich die Mantelfläche und die Gesamtoberfläche. Die von den Flächen eines Prismas eingenommene Fläche, mit Ausnahme der beiden parallelen Flächen (Grundflächen eines Prismas), wird als Mantelfläche bezeichnet.
Die Mantelfläche eines Prismas = [Grundumfang × Höhe] Quadrateinheiten
Die Gesamtoberfläche eines Prismas ist nun die Summe der Flächen seiner beiden Grundflächen und seiner Seitenfläche.
Die allgemeine Formel zur Berechnung der Gesamtoberfläche eines beliebigen Typs eines rechten Prismas lautet:
Die Gesamtoberfläche eines Prismas = [2 (Grundfläche) + (Grundumfang × Höhe)] Quadrateinheiten
Verschiedene Arten von Prismen
Es gibt verschiedene Arten von Prismen, basierend auf der Form der Basis eines Prismas, wie z
- Dreieckige Prismen,
- Quadratische Prismen,
- Rechteckprismen,
- Fünfeckige Prismen,
- Sechseckige Prismen,
- Achteckige Prismen.
Dreieckiges Prisma
Als Dreiecksprisma wird ein Prisma mit dreieckiger Grundfläche bezeichnet. Ein dreieckiges Prisma besteht aus drei geneigten rechteckigen Flächen und zwei parallelen Dreiecksflächen. Sei H die Höhe des dreieckigen Prismas; a, b und c sind die Seitenlängen und h ist die Höhe der dreieckigen Grundflächen.
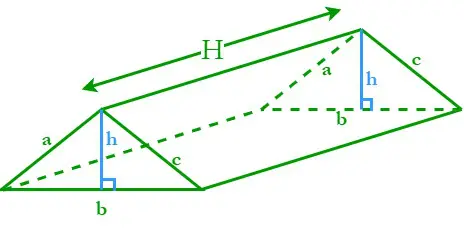
Der Umfang einer dreieckigen Grundfläche (P) = Summe ihrer drei Seiten = a + b + c
Die Fläche einer dreieckigen Grundfläche (A) = ½ × Grundfläche × Höhe = ½ bh
Wir wissen, dass die allgemeine Formel für die Die Seitenfläche eines geraden Prismas ist L. S. A. = PH, wobei P der Basisumfang und A die Basisfläche ist.
Durch Einsetzen aller Werte in die allgemeine Formel erhalten wir ,
Die Mantelfläche eines dreieckigen Prismas = (a + b + c)H Quadrateinheiten
Wo,
Javascript-Datuma, b, c sind Seiten einer dreieckigen Grundfläche
H ist die Höhe des dreieckigen Prismas
Wir wissen, dass die allgemeine Formel für die Gesamtoberfläche eines geraden Prismas lautet T. S. A. = PH+2A, wobei P der Basisumfang, A die Grundfläche und H die Höhe des Prismas ist.
Durch Einsetzen aller Werte in die allgemeine Formel erhalten wir
Die Gesamtoberfläche des dreieckigen Prismas = (a + b + c)H + 2 × (½ bh)
Die Gesamtoberfläche des dreieckigen Prismas = (a + b + c)H + bh Quadrateinheiten
Wo,
a, b, c sind Seiten einer dreieckigen Grundfläche
H ist die Höhe des dreieckigen Prismas
h ist die Höhe des Dreiecks
Rechteckiges Prisma
Ein Prisma mit rechteckiger Grundfläche wird als Rechteckprisma bezeichnet. Ein rechteckiges Prisma besteht aus vier rechteckigen Flächen und zwei parallelen rechteckigen Grundflächen. Die Höhe des Prismas sei h und die Länge und Breite seiner rechteckigen Grundflächen seien l bzw. w .

Der Umfang einer rechteckigen Grundfläche (P) = Summe ihrer vier Seiten = 2 (l + w)
Die Fläche einer rechteckigen Grundfläche (A) = Länge × Breite = L × B
Wir wissen, dass die allgemeine Formel für die Mantelfläche eines geraden Prismas L. S. A. = PH lautet, wobei P der Basisumfang und A die Basisfläche ist.
Durch Einsetzen aller Werte in die allgemeine Formel erhalten wir ,
Die Mantelfläche eines rechteckigen Prismas = 2h(l + w) Quadrateinheiten
Wo,
l ist Länge
w ist die Breite
Seine Größe
Wir wissen, dass die allgemeine Formel für die Gesamtoberfläche eines geraden Prismas T.S.A. = PH+2A lautet, wobei P der Basisumfang, A die Basisfläche und H die Höhe des Prismas ist.
Durch Einsetzen aller Werte in die allgemeine Formel erhalten wir
Die Gesamtoberfläche des rechteckigen Prismas = 2h(l + w) + 2(l × w)
= 2 links + 2 weiß + 2 links
Die Gesamtoberfläche des rechteckigen Prismas = 2 (lh + wh + lw) Quadrateinheiten
Wo,
l ist Länge
w ist die Breite
Seine Größe
Quadratisches Prisma
Ein Prisma mit quadratischer Grundfläche wird als Quadratprisma bezeichnet. Ein quadratisches Prisma besteht aus vier rechteckigen Flächen und zwei parallelen quadratischen Grundflächen. Die Höhe des Prismas sei h und die Länge seiner quadratischen Grundflächen sei s.

Der Umfang einer quadratischen Grundfläche (P) = Summe ihrer vier Seiten = s + s + s + s = 4s
Die Fläche einer quadratischen Grundfläche (A) = (Seitenlänge)2= s2
Wir wissen, dass die allgemeine Formel für die Mantelfläche eines geraden Prismas L. S. A. = PH lautet, wobei P der Basisumfang und A die Basisfläche ist.
Indem wir alle Werte in die allgemeine Formel einsetzen, erhalten wir:
Die Mantelfläche eines quadratischen Prismas = 4sh Quadrateinheiten
Wo,
s ist die Seite der quadratischen Grundfläche
h ist die Höhe des quadratischen Prismas
Wir wissen, dass die allgemeine Formel für die Gesamtoberfläche eines geraden Prismas lautet T. S. A. = PH+2A, Wo P ist der Basisumfang, A ist die Grundfläche und H ist die Höhe des Prismas.
Durch Einsetzen aller Werte in die allgemeine Formel erhalten wir
Die Gesamtoberfläche des quadratischen Prismas = [4sh + 2s 2 ] Quadrateinheiten
Wo,
s ist die Seite der quadratischen Grundfläche
h ist die Höhe des quadratischen Prismas
Fünfeckiges Prisma
Als Fünfeckprisma wird ein Prisma mit fünfeckiger Grundfläche bezeichnet. Ein fünfeckiges Prisma besteht aus fünf geneigten rechteckigen Flächen und zwei parallelen fünfeckigen Grundflächen. Sei h die Höhe des fünfeckigen Prismas; a und b sind die Apothemlänge und Seitenlängen der fünfeckigen Basen.

Der Umfang einer Fünfeckbasis (P) = Summe seiner fünf Seiten = 5b
Die Fläche einer Fünfeckbasis (A) = 5/2 x (Apothemlänge) x (Seitenlänge) = 5ab
Wir wissen, dass die allgemeine Formel für die Mantelfläche eines geraden Prismas L. S. A. = PH lautet, wobei P der Basisumfang und A die Basisfläche ist.
Indem wir alle Werte in die allgemeine Formel einsetzen, erhalten wir:
Die Mantelfläche eines fünfeckigen Prismas = 5bh Quadrateinheiten
Wo,
b ist die Seite der fünfeckigen Basis
h ist die Höhe des fünfeckigen Prismas
Wir wissen, dass die allgemeine Formel für die Gesamtoberfläche eines geraden Prismas T.S.A. = PH+2A lautet, wobei P der Basisumfang, A die Basisfläche und H die Höhe des Prismas ist.
Indem wir alle Werte in die allgemeine Formel einsetzen, erhalten wir:
Die Gesamtoberfläche des fünfeckigen Prismas = [5bh + 5ab] Quadrateinheiten
Wo,
b ist die Seite der fünfeckigen Basis
a ist die Apothemlänge.
h ist die Höhe des fünfeckigen Prismas
Sechseckiges Prisma
Als Sechskantprisma wird ein Prisma mit sechseckiger Grundfläche bezeichnet. Ein sechseckiges Prisma besteht aus sechs geneigten rechteckigen Flächen und zwei parallelen sechseckigen Grundflächen. Sei h die Höhe des sechseckigen Prismas; a seien die Seitenlängen der sechseckigen Grundflächen.

Der Umfang einer Sechseckbasis (P) = Summe seiner sechs Seiten = 6a
Die Fläche einer Sechseckbasis (A) = 6 x (Fläche eines gleichseitigen Dreiecks)
A = 6 x (√3a2/4) ⇒ A = 3√3a2/2
Wir wissen, dass die allgemeine Formel für die Mantelfläche eines geraden Prismas L. S. A. = PH lautet, wobei P der Basisumfang und A die Basisfläche ist.
Indem wir alle Werte in die allgemeine Formel einsetzen, erhalten wir:
Die Mantelfläche eines sechseckigen Prismas = 6ah Quadrateinheiten
Wo,
a ist die Seite der sechseckigen Basis
h ist die Höhe der sechseckigen Basis
Wir wissen, dass die allgemeine Formel für die Gesamtoberfläche eines geraden Prismas T.S.A. = PH+2A lautet, wobei P der Basisumfang, A die Basisfläche und H die Höhe des Prismas ist.
Durch Einsetzen aller Werte in die allgemeine Formel erhalten wir
So ermitteln Sie die Anzeigegröße
Die Gesamtoberfläche des sechseckigen Prismas = [6ah +3√3a2] Quadrateinheiten
Wo,
a ist die Seite der sechseckigen Basis
h ist die Höhe der sechseckigen Basis:
Formel für die Oberfläche des Prismas
Die folgende Tabelle enthält die Formel für verschiedene Prismentypen:
Form | Basis des Prismas | Seitenfläche[Grundumfang × Höhe] | Gesamtoberfläche[(2 × Grundfläche) + (Grundumfang × Höhe)] |
|---|---|---|---|
Dreieckiges Prisma | Dreieck | (a + b +c)H quadratische Einheiten | (a + b + c)H + bh quadratische Einheiten |
Rechteckiges Prisma | Rechteck | 2h(l + w) quadratische Einheiten | 2 (lh + wh + lw) quadratische Einheiten |
Quadratisches Prisma | Quadrat | 4-teilige quadratische Einheiten | [4sh + 2s2] Quadrateinheiten |
Fünfeckiges Prisma | Pentagon | 5bh quadratische Einheiten | [5ab + 5bh] quadratische Einheiten |
Sechseckiges Prisma | Hexagon | 6ah-Quadrateinheiten gültige Bezeichner in Java | [3√3a2+ 6ah] Quadrateinheiten |
Beispiele für gelöste Oberfläche eines Prismas
Aufgabe 1: Wie hoch ist ein Prisma, dessen Grundfläche 36 Quadrateinheiten beträgt, dessen Basisumfang 24 Einheiten beträgt und dessen Gesamtoberfläche 320 Quadrateinheiten beträgt?
Lösung:
Gegebene Daten,
Grundfläche = 36 Quadratmeter
Basisumfang = 24 Einheiten
Die Gesamtoberfläche des Prismas beträgt 320 Quadrateinheiten
Wir haben,
Die Gesamtoberfläche des Prismas = (2 × Grundfläche) + (Grundumfang × Höhe)
⇒ 320 = (2 × 36)+ (24 × h)
⇒ 24h = 248 ⇒ h = 10,34 Einheiten
Daher beträgt die Höhe des gegebenen Prismas 10,34 Einheiten.
Aufgabe 2: Ermitteln Sie die Gesamtoberfläche eines quadratischen Prismas, wenn die Höhe des Prismas und die Seitenlänge der quadratischen Grundfläche 13 cm bzw. 4 cm betragen.
Lösung:
Gegebene Daten,
Die Höhe des quadratischen Prismas (h) = 13 cm
Die Seitenlänge der quadratischen Grundfläche (a) = 4 cm
Wir wissen das,
Die Gesamtoberfläche eines quadratischen Prismas = 2a2+ 4ah
= 2 × (4)2+ 4 × 4 × 13
= 32 + 208 = 240 cm2
Somit beträgt die Gesamtoberfläche des gegebenen Prismas 240 cm².
Aufgabe 3: Bestimmen Sie die Grundlänge eines fünfeckigen Prismas, wenn seine Gesamtfläche 100 Quadrateinheiten beträgt und seine Höhe und Apothemlänge 8 bzw. 5 Einheiten betragen.
Lösung:
Gegebene Daten,
Die Gesamtoberfläche des fünfeckigen Prismas = 100 Quadrateinheiten
Die Höhe des Prismas (h) = 8 Einheiten
Apothemlänge (a) = 5 Einheiten
Wir wissen das,
Die Gesamtoberfläche des fünfeckigen Prismas = 5ab + 5bh
⇒ 100 = 5b (a+ h)
⇒ 100/5 = b (5 + 8)
⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 Einheiten
Daher beträgt die Basislänge 1,54 Einheiten
Problem 4: Bestimmen Sie die Höhe des rechteckigen Prismas und die Gesamtfläche eines rechteckigen Prismas, wenn seine Mantelfläche 540 cm² beträgt und die Länge und Breite der Basis 13 cm bzw. 7 cm betragen.
Lösung:
Gegebene Daten,
Die Länge der rechteckigen Basis (l) = 13 cm
Die Breite der rechteckigen Basis (B) = 7 cm
Die Mantelfläche des Prismas = 540 cm²
Wir haben,
Die Mantelfläche des Prismas = Basisumfang × Höhe
⇒ 540 = 2 (L + B) h
⇒ 2 (13 + 7) h = 540
⇒ 2 (20) h = 540 ⇒ h = 13,5 cm
Wir wissen das,
Die Gesamtoberfläche des rechteckigen Prismas = 2 (lw + wh + lh)
= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))
= 2 × (91 + 94,5 + 175,5) = 722 cm²
Daher betragen die Höhe und die Gesamtoberfläche des gegebenen rechteckigen Prismas 13,5 cm bzw. 722 cm².
Aufgabe 5: Bestimmen Sie die Oberfläche des regelmäßigen sechseckigen Prismas, wenn die Höhe des Prismas 12 Zoll und die Seitenlänge der Basis 5 Zoll beträgt.
Task-Manager für Linux
Lösung:
Gegebene Daten,
Die Höhe des Prismas (h) = 12 Zoll
Die Länge der Seite der Basis (a) = 6 Zoll
Die Oberfläche eines regelmäßigen sechseckigen Prismas = 6ah + 3√3a2
= 6 × 5 × 12 + 3√3(5)2
= 360 + 75√3
= 360 + 75 × (1,732) = 489,9 Quadratzoll
Daher beträgt die Oberfläche des gegebenen Prismas 489,9 Quadratzoll.
Aufgabe 6: Berechnen Sie die Seiten- und Gesamtoberfläche eines dreieckigen Prismas, dessen Basisumfang 25 Zoll beträgt, dessen Basislänge und -höhe 9 Zoll und 10 Zoll beträgt und dessen Höhe 14 Zoll beträgt.
Lösung:
Gegebene Daten,
Die Höhe des Prismas (H) = 14 Zoll
Der Basisumfang des Prismas (P) = 25 Zoll
Die Basislänge des Dreiecks = 9 Zoll
Die Höhe des Dreiecks = 10 Zoll
Wir wissen das,
Die Mantelfläche des Prismas = Basisumfang × Höhe
= 25 × 14= 350 Quadratzoll
Fläche der dreieckigen Basis (A) = ½ × Basis × Höhe = 1/2 × 9 × 10 = 45 Quadratzoll
Die Gesamtoberfläche des dreieckigen Prismas = 2A + PH
= 2 × 45 + 25 × 14 = 90 + 350 = 440 Quadratzoll
Daher betragen die Seiten- und Gesamtflächen des Prismas 350 Quadratzoll bzw. 440 Quadratzoll.
Übungsaufgaben zur Oberfläche eines Prismas
1. Gegeben sei ein rechteckiges Prisma mit den Abmessungen:
- Länge = 6 cm
- Breite = 4 cm
- Höhe = 5 cm
Berechnen Sie die Gesamtoberfläche.
2. Betrachten Sie ein dreieckiges Prisma mit den Abmessungen:
- Basis des Dreiecks = 8 cm
- Höhe des Dreiecks = 6 cm
- Länge des Prismas = 10 cm
Finden Sie die Gesamtoberfläche.
3. Bestimmen Sie die Oberfläche eines regelmäßigen fünfeckigen Prismas mit:
- Seitenlänge der Basis = 7 cm
- Höhe des Prismas = 9 cm.
4. Berechnen Sie die Oberfläche eines sechseckigen Prismas mit:
- Seitenlänge der regelmäßigen sechseckigen Basis = 10 cm
- Höhe des Prismas = 12 cm.
Oberfläche eines Prismas – FAQs
Was ist ein Prisma in der Geometrie?
Ein Prisma ist eine dreidimensionale Form mit zwei kongruenten parallelen Grundflächen und sie verbindenden rechteckigen oder parallelogrammförmigen Seitenflächen. Prismen gibt es in verschiedenen Formen, zum Beispiel als rechteckige Prismen, dreieckige Prismen und fünfeckige Prismen, jede mit einzigartigen Eigenschaften.
Wie findet man die Oberfläche eines Prismas?
Um die Oberfläche eines Prismas zu ermitteln, berechnen Sie die Flächen aller seiner Flächen und summieren sie dann. Für ein rechteckiges Prisma lautet die Oberflächenformel 2lw + 2lh + 2wh, wobei l die Länge, w die Breite und h die Höhe ist. Für andere Prismentypen, beispielsweise dreieckige oder fünfeckige Prismen, sind möglicherweise zusätzliche Formeln für die Grundfläche und die Seitenfläche erforderlich.
Was sind die Eigenschaften eines Prismas?
Prismen haben mehrere Schlüsseleigenschaften:
- Sie haben zwei kongruente parallele Basen.
- Die Seitenflächen sind alle Parallelogramme.
- Die Höhe (Höhe) ist der senkrechte Abstand zwischen den beiden Basen.
- Die Sockel sind in Form und Größe identisch.
- Der Querschnitt parallel zu den Sockeln hat immer die gleiche Form und Größe wie die Sockel.
Was sind einige Beispiele aus der Praxis für Prismen?
Prismen finden sich in verschiedenen Alltagsgegenständen und Strukturen. Beispiele beinhalten:
- Rechteckige Prismen: Gebäude, Müslischachteln, Bücher.
- Dreieckige Prismen: Hausdächer, keilförmige Objekte.
- Fünfeckige Prismen: Einige Säulentypen, bestimmte architektonische Strukturen.
- Sechseckige Prismen: Bestimmte Kristallarten, einige Verpackungsbehälter.
Warum ist die Oberfläche von Prismen wichtig?
Die Oberfläche ist bei Prismen von entscheidender Bedeutung, da sie die Gesamtfläche aller Oberflächen (Flächen) des Prismas darstellt. Das Verständnis der Oberfläche ist bei verschiedenen praktischen Anwendungen hilfreich, beispielsweise bei der Berechnung der Materialmenge, die zum Bau oder der Abdeckung eines prismenförmigen Objekts erforderlich ist, bei der Bestimmung von Wärmeübertragungsraten und bei der Optimierung des Verpackungsdesigns.
