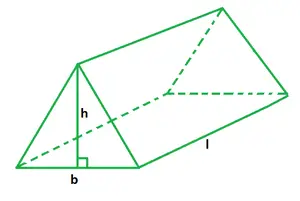
Ein Prisma ist eine dreidimensionale Körperfigur mit zwei identischen Enden. Es besteht aus flachen Seiten, ähnlichen Basen und gleichen Querschnitten. Seine Flächen sind Parallelogramme oder Rechtecke ohne Grundfläche. Ein solches Prisma mit drei rechteckigen Flächen und zwei parallelen dreieckigen Grundflächen wird Dreiecksprisma genannt. Die dreieckigen Grundflächen sind durch parallel zueinander verlaufende Seitenflächen verbunden.

Volumen einer Dreiecksprismenformel

Das Volumen eines dreieckigen Prismas ist definiert als der Raum darin oder der von ihm ausgefüllte Raum. Zur Berechnung seines Volumens ist lediglich die Kenntnis der Grundfläche und der Höhe eines dreieckigen Prismas erforderlich. Das Volumen eines dreieckigen Prismas ist gleich dem Produkt aus der Grundfläche und der Höhe des Prismas, auch Prismenlänge genannt. Die Grundfläche eines dreieckigen Prismas ist gleich der Hälfte des Produkts aus dreieckiger Grundfläche und seiner Höhe.

Formel

V = (1/2) × b × h × l

Wo,

b ist die Dreiecksbasis,

h ist die Höhe des Prismas,

l ist die Länge des Prismas.

Beispielprobleme

Aufgabe 1. Finden Sie das Volumen eines dreieckigen Prismas, wenn seine Grundfläche 6 cm, die Höhe 8 cm und die Länge 12 cm beträgt.

Lösung:

Wir haben b = 6, h = 8 und l = 12.

C#-Codebeispiele

Mit der Formel, die wir haben,

V = (1/2) × b × h × l

= (1/2) × 6 × 8 × 12

= 3 × 8 × 12

= 288 cu. cm

Aufgabe 2. Finden Sie das Volumen eines dreieckigen Prismas, wenn seine Grundfläche 5 cm, die Höhe 7 cm und die Länge 8 cm beträgt.

Lösung:

Wir haben b = 5, h = 7 und l = 8.

Mit der Formel, die wir haben,

V = (1/2) × b × h × l

= (1/2) × 5 × 7 × 8

= 5 × 7 × 4

MySQL-Benutzerliste

= 140 cu. cm

Aufgabe 3. Finden Sie die Länge des dreieckigen Prismas, wenn seine Basis 6 cm, seine Höhe 9 cm und sein Volumen 98 cu beträgt. cm.

Lösung:

Wir haben b = 6, h = 9 und V = 98.

Mit der Formel, die wir haben,

V = (1/2) × b × h × l

=> 98 = (1/2) × 6 × 9 × l

Trennzeichen setzen Java

=> 196 = 27l

=> l = 196/27

=> l = 7,25 cm

Aufgabe 4. Finden Sie die Höhe des dreieckigen Prismas, wenn seine Basis 8 cm, die Länge 14 cm und das Volumen 504 cu beträgt. cm.

Lösung:

Wir haben b = 8, l = 14 und V = 504.

Mit der Formel, die wir haben,

V = (1/2) × b × h × l

=> 504 = (1/2) × 8 × h × 14

=> 504 = 56h

=> h = 504/56

=> h = 9 cm

Aufgabe 5. Finden Sie die Grundfläche des dreieckigen Prismas, wenn seine Länge 18 cm, seine Höhe 10 cm und sein Volumen 450 cu beträgt. cm.

Lösung:

Wir haben l = 18, h = 10 und V = 450.

Mit der Formel für das Volumen, die wir haben,

V = (1/2) × b × h × l

=> 450 = (1/2) × b × 10 × 18

=> 450 = 90b

=> b = 450/90

=> b = 5 cm

schwebend in CSS

Daher ist die Fläche der Dreiecksbasis:

A = (1/2) × b × h

= (1/2) × 5 × 10

= 25 cm²