Mathematik ist ein faszinierendes Fach, das aus einer Vielzahl von Konzepten und Prinzipien besteht. Ein solches Konzept ist Exponentialschreibweise . Die Exponentialschreibweise ist ein grundlegendes Konzept, bei dem eine Basiszahl auf eine bestimmte Potenz (oder einen bestimmten Exponenten) erhöht wird. Dabei handelt es sich um ein leistungsfähiges Konzept, mit dem große und minimale Zahlen besser ausgedrückt werden können. Ein solches Beispiel wird in diesem Artikel besprochen, nämlich 10 bis 5^ThLeistung. In diesem Artikel lernen wir das Konzept der Exponentialschreibweise kennen und diskutieren die Bedeutung der 10 bis 5^ThPower, lernen Sie verschiedene Möglichkeiten kennen, diesen Wert auszudrücken, und diskutieren Sie die Anwendungen der Exponentialschreibweise in verschiedenen Bereichen außerhalb der Mathematik.

Exponentielle Notation definieren

Die exponentielle oder wissenschaftliche Notation bietet eine standardisierte und organisierte Methode zur Darstellung von Zahlen. Es ist von Vorteil, wenn wir mit großen und kleinen Zahlen arbeiten, da es deren Ausdruck vereinfacht und die Klarheit erhöht.

Teile der wissenschaftlichen Notation

Diese Notation besteht aus zwei Teilen:

1. Die Basiszahl
2. Die Exponentenzahl (oder Potenzzahl).

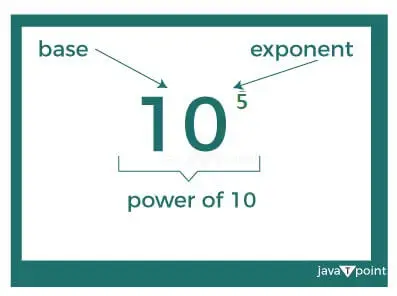
Die Basis ist 10 und der Exponent ist 5, was angibt, wie oft die Basiszahl (10) mit sich selbst multipliziert wird; das impliziert das 10 hoch 5 entspricht 10 multipliziert mit sich selbst 5-mal .

Impliziert 10 x 10 x 10 x 10 x 10 = 10⁵

10 bis 5 ausdrücken^ThLeistung

Es gibt viele Möglichkeiten, 10 hoch 5 auszudrücken oder darzustellen, was auch vom Einsatzgebiet oder den persönlichen Vorlieben abhängt.

Wissenschaftliche Schreibweise:Die einfachste Darstellung ist 10⁵, wobei 10 die Basis und 5 der Exponent oder die Potenz ist; Dieses Format ist normalerweise verständlich und wird häufig in der mathematischen und wissenschaftlichen Literatur verwendet.Numerische Darstellung:Eine andere Möglichkeit, 10 hoch 5 auszudrücken, besteht darin, die Zahl in ihrer erweiterten Form, 100.000, zu schreiben. Dieses Format zerlegt die Zahl in Ziffern und hebt ihre Größe hervor, um ihre Bedeutung zu verstehen.Lange Form:Die Langformdarstellung von 10 hoch 5 ist „one lakh“. Wir verwenden dieses Format in unserer Alltagssprache, damit wir die Zahl leichter verstehen können.

Bedeutsam

10 bis 5^ThMacht war in verschiedenen Bereichen sehr wichtig, vor allem in der wissenschaftlichen Forschung, Technologie und im täglichen Leben; Es stellt den Wert von einem Lakh dar, gleich 1, gefolgt von fünf Nullen, also 100.000. In wissenschaftlichen Notationen wird dieser Wert häufig verwendet, wenn wir große Mengen messen, beispielsweise die Entfernung zwischen Planeten und Himmelsobjekten, die Anzahl der Sterne im Universum und die Weltbevölkerung. Es hilft Wissenschaftlern und Forschern, diese sehr großen Mengen einfacher auszudrücken und erleichtert ihnen das Verständnis und die Analyse dieser Daten.

Bewerbungen vom 10. bis zum 5^ThLeistung

Nachdem wir nun die Berechnung verstanden haben, wollen wir einige praktische Anwendungen untersuchen, bei denen wir die Relevanz der 10 zur 5 ermitteln können^ThLeistung:

Digitale Technologie:In Computern und der Digitaltechnik spielen Zehnerpotenzen eine bedeutende Rolle. Computer speichern und verarbeiten Informationen mithilfe eines Binärcodes, der auf einem zweistelligen System (0 und 1) basiert. Zweierpotenzen, die eng mit Zehnerpotenzen verwandt sind, werden verwendet, um die Größe der Speicherkarte, die Datenübertragungsraten und die Geschwindigkeit der Prozessoren darzustellen.Bevölkerungswachstum:Exponentielles Wachstum wird häufig bei Naturphänomenen, einschließlich Bevölkerungswachstum, beobachtet. Das Konzept von 10 bis 5^ThMacht kann uns helfen zu verstehen, wie die Bevölkerung im Laufe der Zeit schnell wachsen kann; Wenn beispielsweise eine Population von 100.000 Individuen mit einer Rate von 10 % pro Jahr wächst, würde sie nach vier Jahren etwa 14.6410 erreichen.Wissenschaftliche Schreibweise:10 bis 5^ThDie Potenz ist ein entscheidender Bestandteil der wissenschaftlichen Notation. Diese Notation drückt sehr große oder minimale Zahlen in einem handlicheren Format aus.Maßstab und Größe:Zehnerpotenzen werden oft verwendet, um die Größe oder Kleinheit von Objekten oder Phänomenen zu beschreiben. Astronomen verwenden beispielsweise das Konzept eines Lichtjahrs, das die Entfernung angibt, die das Licht in einem Jahr zurücklegt.Berechnen großer Zahlen:In Bereichen wie Finanzen, Physik und Ingenieurwesen sind in der Regel umfangreiche numerische Berechnungen erforderlich. Die Exponentialschreibweise ist für die Vereinfachung dieser Berechnungen hilfreich, da sie eine kompakte Darstellung ermöglicht und die Fehlerwahrscheinlichkeit verringert.

Abschluss

Das Verständnis der Potenzierung ist eine wesentliche Fähigkeit, um Zahlen in verschiedenen Potenzen auszudrücken. In diesem Artikel haben wir untersucht, wie man 10 bis 5 ausdrückt^ThPotenz, was bedeutet, dass 10 fünfmal mit sich selbst multipliziert wird; Das Ergebnis, 100.000, ist ein Grundwert, der in verschiedenen Kontexten erscheint, beispielsweise in der wissenschaftlichen Notation, bei der Umrechnung von Einheiten und in binären Zahlensystemen. Indem wir das Konzept der Exponentialschreibweise und seine praktischen Anwendungen verstehen, können wir die Macht und Fülle (Präsenz) der Mathematik im Alltag besser verstehen.